Das elektrische Feld einer geladenen Metallfläche - Hu

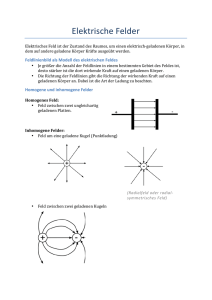
Das elektrische Feld eines geladenen Metallkörpers
1. Im Metall sind Ladungen frei beweglich.
2. Potentialdifferenzen zwischen zwei Punkten einer Metallfläche
werden sofort abgebaut.
3. Daraus ergeben sich folgende Aussagen:
 Es existiert kein elektrisches Feld tangential zur Metallfläche,
d.h.


E t  Dt  0



D N   frei   0 E N  MO   0  r 2 E N 2
 Jede leitende Fläche ist Äquipotentialfläche
 Die Flächenladungsdichte einer geladenen Metallfläche ist
konstant und erzeugt ein Feld senkrecht zur Fläche.
Für das Feld an der Oberfläche gilt:


E N  frei
0
Der Faradaykäfig
 Ein Faradaykäfig ist eine zusammenhängende, hohle
Metallfläche.
 Die Innenfläche ist Äquipotentialfläche, d.h. V = const. 


V( ri )  V( rj )  0
für jeden Ort r der Metallfläche.
 Die Feldstärke im Inneren des Käfigs ist Null. Dies folgt sofort
aus dem Gauß’schen Satz, da die Ladung im Inneren des
Hohlraumes Null ist. 
Die Relation V = const. gilt für den gesamten Hohlraum und
nicht nur für die Innenfläche.
 Die gesamte Oberflächenladung sammelt sich auf der
Außenfläche und erzeugt ein E-Feld senkrecht zur Oberfläche.
Das elektrische Feld einer geladenen Metallfläche

E




E


E



dA




E

 dA
Mit Hilfe des Gauss’schen Satzes
  Q
 EdA  0
findet man
  

   

Q
E
d
A

E

A


E


A

 2EA

0
Da sich die Normalkomponente des elektrischen Feldes aus der
Oberflächenladungsdichte E = /0 ergibt, folgt:
E

2 0