11 Lagrangesche Mechanik

11 Lagrangesche Mechanik
In diesem Kapitel werden wir den ersten Schritt zu einer allgemeinen Formulierung aller heute bekannten
fundamentalen physikalischen Theorien machen. Allerdings ist dieser erste Schritt sehr bescheiden. Wir
werden im Prinzip nichts anderes tun als die Newtonschen Bewegungsgleichungen in einer mathematisch
etwas anspruchsvolleren, “geometrischen” Form aufzuschreiben.
Diese neue Formulierung der Newtonschen Mechanik wurde im 18. Jahrhundert entwickelt und geht
im wesentlichen auf d’Alembert, Lagrange und Euler zurück. Sie ist begrifflich sehr viel abstrakter als
die Newtonsche Formulierung, bietet aber eine Reihe von praktischen und konzeptionellen Vorteilen. Ein
wichtiger, ganz pragmatischer Vorteil ist, dass sich typische mechanische Systeme, wie sie in technischen
Anwendungen auftreten, sehr viel effizienter berechnen lassen als mit den Newtonschen Mitteln.
Eine andere, für die theoretische Physik besonders wichtige Eigenschaft der neuen Formulierung ist,
dass sich mit ihr viele allgemeine Sätze beweisen lassen, mir deren Hilfe sich Aussagen über die Lösungen von Bewegungsgleichungen machen lassen, auch wenn man diese nicht explizit angeben kann. Der
wohl wichtigste derartige Satz ist das Noether-Theorem, wonach es einen Zusammenhang zwischen den
Symmetrien eines Systems und seinen Erhaltungsgrößen. Bis wir zu diesem zentralen Theorem kommen,
müssen wir uns allerdings erst mit einigen neuen Begriffen vertraut machen.
Die Methoden, die wir hier entwickeln werden, lassen sich weit über die Mechanik hinaus auch in
anderen Teilgebieten der Physik anwenden. Daher werden uns die Begriffe, die wir in diesem Kapitel
einführen, fast überall wieder begegnen. Wie schon angedeutet, geht dies sogar so weit, dass sich alle
heute als fundamental angesehenen Theorien in dieses Schema einordnen lassen. Einen Hinweis darauf,
dass zum Beispiel auch die Elektrodynamik eine solche Formulierung zulässt, wird sich am Ende dieses
Kapitels ergeben. Ansonsten werden wir uns hier jedoch nur mit mechanischen Systemen beschäftigen.
Energie und Impuls
Bei der allgemeinen Diskussion der Newtonschen Bewegungsgleichungen für ein System von Punktteilchen hatten wir die Impulse der Teilchen als nützlich Hilfsgrößen eingeführt. Damit konnten wir ein System von Differenzialgleichungen zweiter Ordnung in ein System erster Ordnung überführen. Außerdem
gab es für Systeme ohne äußere Kräfte einen Erhaltungssatz für den Gesamtimpuls, also für die Summe
der Impulse aller Teilchen. Das konnten wir verwenden, um die Bewegungsgleichungen weiter zu vereinfachen und um deren Lösungen zu klassifizieren.
Den Impuls hatten wir als das Produkt von Masse und Geschwindigkeit definiert, weil so seine Zeitableitung durch die Kraft gegeben war, die auf ein Teilchen einwirkt. Wir wollen nun zeigen, dass es noch
eine alternative Definition der Größe “Impuls” gibt. Diese wird sich später als sehr viel allgemeiner erweisen. Sie ist weit über die Mechanik hinaus anwendbar. Sie gibt dem Begriff “Impuls” eine ähnlich wichtige
Bedeutung wie etwa dem Begriff “Energie”, der ja auch in allen Bereichen der Physik von zentraler Bedeutung ist.
Tatsächlich lässt sich der Impuls eines Teilchens aus seiner Energie ableiten, und zwar im wahrsten
Sinne des Wortes. Stellen wir die Geschwindigkeit des Teilchens der Masse m in einem kartesischen
Koordinatensystem durch v = vi ei dar, so ist seine kinetische Energie
T =
1
1
m v · v = m vi vi .
2
2
(11.1)
Es ist üblich, die Funktion, die der Geschwindigkeit die kinetische Energie zuordnet, mit T zu bezeichnen.
Wenn wir sie partiell nach den Komponenten der Geschwindigkeit ableiten, bekommen wir
∂T
= m vi = pi ,
∂vi
42
(11.2)
also die Komponenten des Impulses. Der Impuls ist die Ableitung der Energie nach der Geschwindigkeit.
Das lässt sich verallgemeinern. Für ein System von N Teilchen mit Massen m n ist die gesamte kinetische Energie eine Funktion der Geschwindigkeiten vn = vn,i ei der einzelnen Teilchen,
T =
1X
1X
m n vn · v n =
mn vn,i vn,i .
2 n
2 n
(11.3)
Die Funktion T hängt jetzt von 3 N reellen Variablen ab, nämlich den Komponenten der Geschwindigkeiten vn,i , mit n ∈ {1, . . . , N } als Teilchenindex und i ∈ {x, y, z} als Vektorindex. Für Vektorindizes
soll wieder die Summenkonvention gelten, und da wir eine Orthonormalbasis verwenden, können wir alle
Indizes nach unten schreiben.
Bilden wir nun wieder die partiellen Ableitungen der Funktion T , so finden wir
∂T
= mn vn,i = pn,i .
∂vn,i
(11.4)
Das sind die Komponenten des Impulses des Teilchens Nummer n. Wir können auf diese Weise durch
Ableiten der kinetischen Energie eines Systems von beliebig vielen Teilchen jedem einzelnen Teilchen
seinen Impuls zuordnen.
Der Impuls eines Teilchens ist die Ableitung der kinetischen Energie nach der Geschwindigkeit dieses Teilchens.
Wie sich gleich zeigen wird, ist es an dieser Stelle ganz wesentlich, dass es sich um eine Funktion T
handelt, die von den Geschwindigkeiten aller Teilchen abhängt. Die Funktion T ist also dem System als
ganzes zugeordnet, nicht den einzelnen Teilchen.
Die Bewegungsgleichungen lassen sich nun wie folgt formulieren. Die Teilchen bewegen sich auf Bahnen rn (t), oder in kartesischen Koordinaten rn,i (t). Dann ist natürlich vn (t) = ṙn (t) bzw. vn,i (t) = ṙn,i (t),
und somit
∂T
∂T (t).
(11.5)
=
pn,i (t) =
∂vn,i n = ˙ n (t) ∂ ṙn,i
Der Ausdruck ist so zu verstehen, dass wir erst die Funktion T nach v n,i ableiten, und dann diese Funktion
für vn = ṙn (t) auswerten, also die gegebene Bahnkurve einsetzen, so dass der Ausdruck zu einer Funktion
der Zeit wird. Um die Notation etwas zu verkürzen, schreiben wir dafür auch einfach ∂T /∂ ṙ n,i .
Jetzt müssen wir den Impuls nur noch nach der Zeit ableiten und mit der Kraft gleichsetzen,
d ∂T
ṗn,i (t) =
(t) = Fn,i (t).
(11.6)
dt ∂ ṙn,i
Die Kräfte Fn = Fn,i ei sind in der Regel als Funktionen der Orte und der Geschwindigkeiten gegeben.
Setzen wir wieder die Bahnen rn (t) ein, so ergibt sich eine Funktion der Zeit, die die Ableitung des
Impulses nach der Zeit bestimmt. Die Gleichungen (11.6) bilden dann ein System von 3 N gekoppelten
Differenzialgleichungen zweiter Ordnung für die Koordinatenfunktionen r n,i (t). Dies sind natürlich die
bekannten Newtonschen Bewegungsgleichungen.
Auf den ersten Blick scheint damit nicht viel gewonnen zu sein. Genau genommen sehen die Gleichungen (11.6) sogar ziemlich kompliziert aus, nicht zuletzt wegen der etwas verschachtelten Ableitungen.
Was allerdings auffällt, ist, dass die Massen mn anscheinend aus den Bewegungsgleichungen verschwunden sind. Natürlich sind sie nicht wirklich verschwunden. Aber sie gehen jetzt nur noch implizit über die
Definition der Funktion T ein.
In den Newtonschen Formulierung der Bewegungsgleichungen ist die Masse ein Maß für die Trägheit
eines Teilchens, also das Verhältnis von Impuls zu Geschwindigkeit. Hier ist die Masse statt dessen ein
43
Maß für die kinetische Energie, die ein bewegtes Teilchen besitzt, und der Impuls ist definiert als die
Ableitung der Energie nach der Geschwindigkeit. Das ändert an den mathematischen Zusammenhängen
zwischen diesen Größen nichts, bietet aber eine alternative Interpretation der Begriffe.
Aufgabe 11.1 Wir nehmen an, dass die Kräfte konservativ sind und nur von den Orten der Teilchen
abhängen. Dann existiert ein Potenzial V, das eine Funktion der Orte r n ist, und die Kraft Fn ist der
negative Gradient von V bezüglich des Ortes rn . Folglich gelten die Bewegungsgleichungen
d ∂T
∂V
(t) = Fn,i (t) = −
(t).
(11.7)
dt ∂ ṙn,i
∂rn,i
Andererseits wissen wir, dass in diesem Fall die Energie E = T + V eine Erhaltungsgr öße ist. Man zeige,
dass sich dies aus (11.7) ergibt, wobei man nur annehmen muss, dass die Funktion T rein quadratisch ist,
also homogen vom Grad 2 in den Komponenten den Geschwindigkeiten.
Der Konfigurationsraum
Die Bewegungsgleichungen in der Form (11.6) lassen sich etwas einfacher darstellen, wenn wir das folgende neue Konzept einführen. Wir fassen die Ortskoordinaten r n,i aller N Teilchen als Koordinaten eines
Punktes in einem 3 N -dimensionalen Raum auf. Diesen Raum nennen wir den Konfigurationsraum des
Systems, und wir bezeichnen ihn mit Q.
Der Konfigurationsraum besteht aus allen möglichen Anordnungen der Teilchen im Ortsraum, das heißt
aus allen möglichen Konfigurationen von N Teilchen. Einen Punkt in diesem Raum bezeichnen wir mit
q ∈ Q, und seine Koordinaten mit q µ , wobei µ ein laufender Index ist, der 3 N Werte annimmt. Um
die Beziehung zu den einzelnen Teilchen deutlich zu machen, können wir als Indexmenge die Symbole
µ ∈ {x1 , y1 , z1 , x2 , y2 , z2 , . . . , xN , yN , zN } verwenden. Wir können die Koordinaten aber auch einfach
von 1 bis 3 N durchnummerieren. Wir sagen, dass ein System aus N Teilchen 3 N Freiheitsgrade besitzt.
Die Zahl der Freiheitsgrade eines mechanischen System ist die Dimension des Konfigurationsraumes,
dim Q = 3 N .
Wir schreiben den Index bei q µ nach oben, weil der Konfigurationsraum im allgemeinen kein metrischer
Raum ist. Wir können zwar den Abstand zwischen zwei Punkten oder zwei Teilchen im Ortsraum messen.
Es ist aber eine völlig andere Frage, was unter dem “Abstand” von zwei verschiedenen Konfigurationen
von N Teilchen zu verstehen ist. Jedenfalls gibt es keine unmittelbar auf der Hand liegende Antwort auf
die Frage, wie weit zwei Konfigurationen voneinander entfernt sind. Es gibt auf dem Konfigurationsraum
keine Metrik, folglich auch keine kartesischen Koordinaten, und deshalb müssen wir zwischen Vektoren
und dualen Vektoren unterscheiden.
Wie wird nun die Zeitentwicklung des Systems beschreiben? Offenbar durch eine Bahn q(t) im Konfigurationsraum Q, die zu jedem Zeitpunkt angibt, welche Konfiguration das System gerade einnimmt.
Sie wird explizit durch die Koordinatenfunktionen q µ (t) dargestellt. Das ist eine parametrisierte Kurve in
einem affinen Raum. Wir können daher den Tangentenvektor q̇(t) bilden, dessen Komponenten durch die
Ableitungen q̇ µ (t) gegeben sind. Dies ist ein Vektor in dem zugeordneten Vektorraum TQ des Konfigurationsraumes Q. Um die Sprechweise möglichst einfach zu halten, nennen wir q(t) den Ort und q̇(t) die
Geschwindigkeit des Systems zum Zeitpunkt t. Wir fassen quasi alle Orte der Teilchen zu einem Ort in Q
zusammen, und alle Geschwindigkeiten der Teilchen zu einem Geschwindigkeitsvektor in TQ.
Die oben eingeführte alternative Formulierung der Bewegungsgleichungen für ein System aus N Teilchen stellt sich jetzt wie folgt dar. Zuerst definieren wir die kinetische Energie als Funktion der Geschwindigkeiten der Teilchen, das heißt als Funktion eines Vektors q̇ ∈ TQ. Sie ist eine quadratische Funktion
der Komponenten q̇ µ , die sich ganz allgemein wie folgt schreiben lässt,
T =
1
Mµν q̇ µ q̇ ν .
2
44
(11.8)
Die 3 N ×3 N -Matrix Mµν ist die Massenmatrix des Systems. Für den hier beschriebenen Fall hat sie eine
einfache Diagonalform


m1
m1
0



m1



.
.
Mµν = 
(11.9)
.
.


m
N


0
mN
mN
Ihre Einträge sind die Massen der einzelnen Teilchen, wobei jede Masse genau dreimal auftritt, entsprechend den drei Komponenten der Geschwindigkeit, die zu diesem Teilchen gehören. Schreibt man die
Summe über µ und ν in (11.8) explizit aus, so findet man wieder den Ausdruck (11.3).
Dass wir die Massen zu einer Matrix mit zwei unteren Indizes zusammengefasst haben, ist im wesentlichen dadurch motiviert, dass sich diese Matrix nun wie ein symmetrischer Tensor der Stufe (0, 2)
auf dem Konfigurationsraum Q verhält. Durch (11.8) wird eine symmetrische, bilineare Abbildung
M : TQ × TQ → R definiert, so dass T = M (q̇, q̇)/2 ist. Wir werden darauf gleich noch näher
eingehen.
Im nächsten Schritt definieren wir die Impulse, indem wir die partiellen Ableitungen der Funktion T
nach den Komponenten q̇ µ der Geschwindigkeit bilden. Das ergibt
pµ =
∂T
= Mµν q̇ µ .
∂ q̇ µ
(11.10)
Wie man leicht durch Einsetzen der Matrix (11.9) bestätigt, sind das die 3 N Komponenten der Impulse
der einzelnen Teilchen. Diese können wir wieder zu einem 3 N -dimensionalen Vektor zusammenfassen.
Aus (11.10) ergibt sich jedoch, dass die Komponenten pµ ihren Index unten tragen. Folglich ist die Geschwindigkeit q̇ ∈ TQ ein Vektor, während der Impuls p ∈ T∗ Q des Systems ein dualer Vektor ist.
Da die Kraft die Zeitableitung des Impulses ist, muss auch das ein dualer Vektor F ∈ T ∗ Q sein. Es gilt,
in Komponenten aufgeschrieben,
d ∂T
(t)
= Fµ (t).
(11.11)
ṗµ (t) =
dt ∂ q̇ µ
Genau wie die Komponenten pµ des Impulses p ergeben sich die 3 N Komponenten Fµ der Kraft F aus
den ursprünglichen Komponenten Fn,i dadurch, dass wir sie einfach nur neu nummerieren. Wir fassen
den Teilchenindex n und den Vektorindex i zu einem einzigen Vektorindex µ zusammen, der 3 N Werte
annimmt.
Inhaltlich ändert sich an den Bewegungsgleichungen nichts. Es handelt sich noch immer um ein Gleichungssystem für 3 N unbekannte Funktionen, nur dass wir diese jetzt mit q µ (t) bezeichnen. Die Kraft F
ist typischerweise als Funktion des Ortes q und der Geschwindigkeit q̇ gegeben, und sie kann natürlich
auch explizit von der Zeit abhängen. Erst durch Einsetzen einer Bahn q(t) wird daraus eine Funktion, die
nur noch von der Zeit anhängt. Das gleiche gilt für den Impuls. Die partielle Ableitung ∂T /∂ q̇ µ ist eine
Funktion der Geschwindigkeit q̇, und durch Einsetzen einer Bahn q(t) wird sie zu einer Funktion der Zeit.
Dass Kraft und Impuls duale Vektoren auf dem Konfigurationsraum sind, lässt sich auch noch auf eine ganz andere Weise erklären. Für konservative Systeme ist die Kraft der Gradient des Potenzials. Die
potenzielle Energie eines N -Teilchen-Systems ist eine Funktion der Orte der Teilchen, also eine skalare
Funktion V auf dem Konfigurationsraum. Folglich ist der Gradient davon ein dualer Vektor, oder genauer
ein duales Vektorfeld auf Q. Für konservative Systeme, deren Kräfte nur vom Ort abhängen, gilt
∂V
∂V
d ∂T
Fµ = µ ⇒ ṗµ (t) =
(t)
= µ (t).
(11.12)
∂q
dt ∂ q̇ µ
∂q
45
Damit hier die rechte und die linke Seite der Gleichung zusammenpassen, muss auf beiden Seiten ein
dualer Vektor stehen. Das ist auch der Fall, und es impliziert, dass auch der Impuls in dualer Vektor sein
muss.
Damit haben wir bereits die wichtigsten Begriffe eingeführt, die wir zur systematischen Beschreibung
eines allgemeinen mechanischen Systems benötigen.
Die Konfiguration eines mechanischen Systems wird durch einen Punkt im Konfigurationsraum dargestellt. Die Geschwindigkeit ist ein Vektor, Impuls und Kraft sind duale Vektoren
in diesem Raum.
Um ein konkretes mechanisches System zu beschrieben, benötigen wir zwei Informationen über das System. Wir müssen erstens wissen, wie die Geschwindigkeiten mit den Impulsen zusammenhängen. Dies
geschieht durch die Abgabe der Funktion T , die die kinetische Energie als Funktion der Geschwindigkeiten darstellt. Für ein N -Teilchen-System bedeutet das im wesentlichen, dass wir die Massen der Teilchen
kennen müssen. Und wir müssen natürlich zweitens wissen, wie die Kraft F konkret als Funktionen des
Ortes q, der Geschwindigkeit q̇ und der Zeit t gegeben ist. Für ein System mit Potenzialkräften ist das
äquivalent zur Angabe der Potenzialfunktion V.
Aufgabe 11.2 Man betrachte ein System aus drei Teilchen mit Massen m 1 , m2 und m3 , die sich gegenseitig
durch Gravitationskräfte anziehen. Wie sieht in diesem Fall das Potenzial aus? Man mache sich an diesem
Beispiel klar, dass es sich um eine reelle Funktion V auf einem neundimensionalen Raum Q handelt.
Aufgabe 11.3 Die Massenmatrix Mµν eines mechanischen Systems ist symmetrisch und positiv, da die
kinetische Energie stets positiv ist und nur dann gleich Null, wenn alle Teilchen ruhen. Man kann sie
daher als Metrik auf dem Konfigurationsraum interpretieren, der dadurch zu einem metrischen affinen
Raum wird. Wenn man dies tut, welche anschauliche Vorstellung verbindet sich dann mit dem Abstand von
zwei Konfigurationen? Wann liegen zwei gegebene Konfigurationen nahe beieinander, wann sind sie weit
voneinander entfernt?
Ein einfaches Beispiel
Um den Begriff des Konfigurationsraumes etwas besser zu verstehen, betrachten wir ein einfaches Beispiel. Zwei Teilchen wechselwirken miteinander durch eine linear vom Abstand abhängende Kraft. Es
handelt sich im wesentlichen um einen harmonischen Oszillator, der aus zwei Teilchen besteht. Um das
ganze so einfach wie möglich zu halten, und um das Ergebnis auch grafisch darstellen zu können, sollen
sich die Teilchen nur in eine Raumrichtung bewegen. Dadurch sparen wir uns das Ausschreiben einiger
Indizes, verlieren jedoch keine wesentlichen Aspekte von dem, worum es hier gehen soll.
Es seien also m1 und m2 die Massen der beiden Teilchen, q 1 und q 2 ihre Ortskoordinaten, und q̇ 1 und
2
q̇ die Geschwindigkeiten. Die Orte q µ , mit µ ∈ {1, 2}, sind die Koordinaten eines Punktes q ∈ Q,
wobei der Konfigurationsraum Q ein zweidimensionaler affiner Raum ist. Die Geschwindigkeiten q̇ µ sind
entsprechend die Komponenten eines Vektors q̇ ∈ TQ.
Für die kinetische und die potenzielle Energie setzen wir
T =
1
1
m1 (q̇ 1 )2 + m2 (q̇ 2 )2 ,
2
2
V=
1
κ (q 1 − q 2 )2 ,
2
(11.13)
wobei κ eine Federkonstante ist, die die Anziehungskraft zwischen den beiden Teilchen bestimmt. Für die
Impulse ergibt sich daraus, wie nicht anders zu erwarten ist,
p1 =
∂T
= m1 q̇ 1 ,
∂ q̇ 1
p2 =
46
∂T
= m2 q̇ 2 ,
∂ q̇ 2
(11.14)
und für die Komponenten der Kraft gilt
F1 = −
∂V
2
1
1 = κ (q − q ),
∂q
F2 = −
∂V
1
2
2 = κ (q − q ).
∂q
(11.15)
Die Teilchen ziehen sich mit einer linear mit dem Abstand ansteigenden Kraft an. Schließlich ergeben sich
aus dieser Gleichung und der vorigen die Bewegungsgleichungen
ṗ1 = F1 ,
ṗ2 = F2
⇒
m1 q̈ 1 = κ (q 2 − q 1 ),
m2 q̈ 2 = κ (q 1 − q 2 ).
(11.16)
Wir wissen bereits, wie wir diese Gleichungen am einfachsten lösen können. Die Idee besteht im wesentlichen darin, die Bewegung des Schwerpunktes von der relativen Bewegung der Teilchen zu entkoppeln.
Das neue ist, dass wir dies nun als Koordinatentransformation auf dem Konfigurationsraum Q auffassen
können. Die Transformation, die hier zum Ziel führt, ist
q+ =
m2
m1
q1 +
q2,
m1 + m 2
m1 + m 2
q− = q1 − q2,
(11.17)
oder umgekehrt
m2
m1
q −,
q2 = q+ −
q−.
(11.18)
m1 + m 2
m1 + m 2
Da es sich um eine lineare Transformation handelt, gelten die gleichen Umrechnungsformel auch für die
Geschwindigkeiten. Wir müssen nur alle q’s mit einem Punkt versehen, oder einfach die Gleichungen
(11.17) und (11.18) nach der Zeit ableiten. Nach einer kurzen Rechnung findet man dann die folgenden
neuen Ausdrücke für die kinetische und die potenzielle Energie,
q1 = q+ +
T =
1
1
m+ (q̇ + )2 + m− (q̇ − )2 ,
2
2
V=
1
κ (q − )2 ,
2
(11.19)
wobei wir die Abkürzungen
m1 m2
(11.20)
m1 + m 2
für die gesamte und die reduzierte Masse eingeführt haben. Wiederholen wir jetzt die ganze Prozedur noch
einmal, so finden wir die Impulse
m+ = m 1 + m 2 ,
p+ =
m− =
p− =
∂T
= m− q̇ − ,
∂ q̇ −
(11.21)
F− = −
∂V
= −κ q − .
∂q −
(11.22)
∂T
= m+ q̇ + ,
∂ q̇ +
und für die Komponenten der Kraft gilt jetzt
F+ = −
∂V
= 0,
∂q +
Daraus lesen wir wieder die Bewegungsgleichungen ab. Sie haben sich ein wenig vereinfacht und lauten
nun
ṗ+ = F+ , ṗ+ = F+ ⇒ m+ q̈ + = 0,
m− q̈ − = −κ q − .
(11.23)
Die Lösungen dieser Gleichungen können wir sofort angeben. Für q + müssen wir eine gleichförmige
Bewegung einsetzen, das heißt das System bewegt sich mit konstanter Geschwindigkeit in Richtung der
q + -Achse. In Richtung der q − -Achse finden wir eine harmonische Oszillation mit der Eigenfrequenz ω 2 =
κ/m− .
Was haben wir bei dieser Herleitung anders gemacht als früher, als wir ein solches System schon einmal
im Rahmen der Newtonschen Mechanik diskutiert haben? Der wesentliche Unterschied liegt darin, dass
47
q2
q+
replacements
q1
q−
(c)
(d)
(b)
(a)
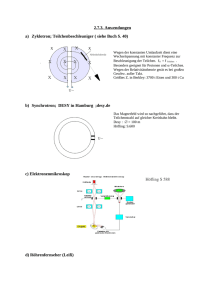
Abbildung 11.1: Der Konfigurationsraum eines Zwei-Teilchen-Systems mit linearer Wechselwirkung. Die
gestrichelten Geraden sind die Linien konstanter potenzieller Energie V = konst. Die gestrichelte Ellipse
ist eine Linie konstanter kinetischer Energie T = konst im Raum der Geschwindigkeiten. Die durchgezogene Linie ist eine typische Bahn. Die Koordinaten in (a) sind den Teilchen angepasst, die Koordinaten
in (b) den Eigenmoden des Systems.
wir an keiner Stelle die Bewegungsgleichungen selbst transformiert haben. Wir haben nicht die Definitionen (11.18) der neuen Koordinaten in die Bewegungsgleichungen (11.16) eingesetzt. Statt dessen haben
wir nur die zwei Größen, von denen wir ausgegangen sind, nämlich die Funktionen T und V, durch die
neuen Koordinaten ausgedrückt.
In Abbildung 11.1(a) ist der zweidimensionale Konfigurationsraum Q mit der q 1 - und q 2 -Achse dargestellt. Das Potenzial V(q) hängt nur von q 1 − q 2 ab, so dass die Linien mit V = konst Geraden sind, die
parallel zur Winkelhalbierenden verlaufen. Die Linien T = konst im Raum TQ der Geschwindigkeiten
sind Ellipsen, deren Halbachsen durch die Massen m1 und m2 bestimmt sind. Eine solche Ellipse ist in
der Abbildung eingezeichnet.
Nun hatten wir gesehen, dass die Dynamik des Systems, also letztlich die Bewegungsgleichungen, eindeutig durch die beiden Funktion T und V bestimmt wird. Insbesondere ist das dynamische Verhalten des
Systems völlig unabhängig davon, welche Koordinaten wir benutzen, um eine explizite Rechnung durchzuführen. Die Dynamik des Systems ist ein Art geometrische Eigenschaft des Konfigurationsraumes, die
unabhängig von der Wahl irgendeines Koordinatensystems ist, genau wie die Geometrie des Ortsraumes
als abstrakte Struktur unabhängig von den Koordinatensystemen ist, die wir verwenden, um den Raum zu
beschreiben.
Wir können deshalb zu einem beliebigen anderen Koordinatensystem übergehen, das der Dynamik des
Systems besser angepasst ist. Ein solches Koordinatensystem ist in Abbildung 11.1(b) dargestellt. Die q + Achse ist so gewählt, dass sie im Minimum des Potenzials liegt. Daher hängt die Funktion V jetzt nur
noch von q − ab, und zwar unabhängig davon, in welche Richtung die q − -Achse zeigt. Aber auch für diese
Achse gibt es eine bevorzugte Wahl. Sie ist so gelegt, dass in dem quadratischen Ausdruck für T keine
gemischten Terme auftreten, die das Produkt q̇ + q̇ − enthalten.
Aufgabe 11.4 Man zeige, dass die lineare Transformation (11.17) durch diese beiden Forderungen an die
neuen Koordinaten q + und q − bis auf Skalierungen eindeutig festgelegt ist. Die einzige Freiheit, die noch
bleibt, ist eine Transformation q̃ + = α q + und q̃ − = β q − mit Konstanten α, β 6= 0.
48
Das abstrakte Konzept des Konfigurationsraumes eines mechanischen Systems kann also bei der Lösung
der Bewegungsgleichungen hilfreich sein. Es zeigt nämlich, dass die Koordinaten, die sich auf natürliche
Weise aus der physikalischen Situation ergeben, nicht immer die sind, die dem eigentlichen dynamischen
Prozess am besten angepasst sind. In unserem Beispiel liegt es durch die Beschreibung des Systems eigentlich auf der Hand, dass die “natürlichen” Koordinaten diejenigen sind, die sich auf die beiden Teilchen
beziehen, also (q 1 , q 2 ).
Lassen wir jedoch die physikalische Anschauung für einen Moment außer acht, und betrachten nur die
mathematischen Strukturen des Konfigurationsraumes Q, so stellen wir fest, dass diese eine ganz andere
“natürliche” Wahl der Koordinaten nahe legen, nämlich die Koordinaten (q + , q − ). In diesen Koordinaten
nehmen die beiden für die Dynamik relevanten Funktionen T und V eine besonders einfache Form an.
Das Ziel der folgenden Überlegungen ist es deshalb, von der unmittelbaren physikalischen Vorstellung
Abstand zu nehmen, dass die Bewegungen eines mechanischen Systems im dreidimensionalen Ortsraum
stattfinden. Statt dessen wollen wir den Konfigurationsraum als denjenigen Raum betrachten, in dem sich
das System bewegt. Das ist der erste Schritt hin zu einer Abstraktion, die es letztlich auch ermöglicht,
ganz andere dynamische Systeme, wie etwa das elektromagnetische Feld, mit den gleichen Methoden zu
beschreiben und dabei die gleichen mathematischen Strukturen zu verwenden.
Aufgabe 11.5 Es soll ein System von zwei Teilchen gleicher Masse m betrachtet werden, die zus ätzlich
eine lineare rücktreibende Kraft von außen spüren. Diese soll eine Federkonstante κ haben, die Wechselwirkung eine Federkonstante κ̃. Es ist dann
T =
1
m (q̇ 1 )2 + (q̇ 2 )2 ,
2
V=
1
1
κ (q 1 )2 + (q 2 )2 + κ̃ (q 1 − q 2 )2 .
2
2
(11.24)
Man finde eine lineare Transformation zu neuen Koordinaten (q + , q − ), so dass
T =
1
1
m+ (q̇ + )2 + m− (q̇ − )2 ,
2
2
V=
1
1
κ+ (q + )2 + κ− (q − )2
2
2
(11.25)
gilt. Man bestimme die Größen m± und κ± , und daraus die Eigenfrequenzen ω± des System. Sind die
neuen Koordinaten eindeutig bestimmt? Wenn nicht, welche Freiheiten gibt es bei der Wahl?
Aufgabe 11.6 Man wiederhole die einzelnen Schritte in diesem Abschnitt f ür ein System von zwei Teilchen,
die sich im dreidimensionalen Raum bewegen. Um die Zerlegung in Schwerpunkt- und Relativbewegung
durchzuführen, hatten wir in Kapitel 3 den Schwerpunktimpuls (3.53) und den relativen Impuls (3.54)
eingeführt. Man zeige, dass diese Größen den hier definierten Impulsen p+ und p− entsprechen.
Aufgabe 11.7 Der Übergang zwischen den beiden Koordinatensystemen (q 1 , q 2 ) und (q + , q − ) ist eine
affine Koordinatentransformation auf dem Konfigurationsraum Q. Man zeige, dass der Impuls und die
Kraft dabei wie duale Vektoren transformieren. Es gilt also
pα =
∂q µ
pµ ,
∂q α
bzw. pµ =
∂q α
pα ,
∂q µ
mit µ ∈ {1, 2},
α ∈ {+, −},
(11.26)
und entsprechend für Fµ und Fα .
Aufgabe 11.8 Sowohl in (11.13) als auch in (11.19) lässt sich die kinetische Energie durch eine Massenmatrix darstellen. Mit den Bezeichnungen aus Aufgabe 11.7 gilt f ür die Einträge dieser Matrix in den
beiden Koordinatensystemen
M11 = m1 ,
M22 = m2 ,
bzw. M++ = m+ ,
49
M−− = m− ,
(11.27)
und alle anderen Komponenten sind jeweils Null. Man verifiziere, dass f ür diese Matrix das Transformationsverhalten für einen Tensor der Stufe (0, 2) gilt, also
Mαβ =
∂q µ ∂q ν
Mµν ,
∂q α ∂q β
(11.28)
wieder mit µ ∈ {1, 2} und α ∈ {+, −}.
Aufgabe 11.9 In Abbildung 11.1(a) stehen die Koordinatenachsen senkrecht aufeinander, in Abbildung 11.1(b) nicht. Hat dieser Umstand irgendeine Bedeutung?
Aufgabe 11.10 Ist in Abbildung 11.1 m1 oder m2 die größere Masse?
Verallgemeinerte Koordinaten
Wir kehren nun wieder zu der allgemeinen Situation zurück, die bei einem N -Teilchen-System mit beliebigen Wechselwirkungen vorliegt. Die kinetische Energie T ist dann eine quadratische Funktion der
Geschwindigkeit q̇ ∈ TQ, und die Kraft ist ein dualer Vektor F ∈ T∗ Q, der zunächst vom Ort q ∈ Q, der
Geschwindigkeit q̇ ∈ TQ, und möglicherweise auch von der Zeit t abhängt. Weitere Annahmen machen
wir nicht. Insbesondere muss die Kraft nicht konservativ sein.
Dann gelten, wie wir gezeigt haben, die Bewegungsgleichungen (11.11), also
d ∂T
= Fµ .
dt ∂ q̇ µ
(11.29)
Wir erinnern noch einmal daran, was die Notation bedeutet. Die linke Seite ist so zu verstehen, dass wir
zuerst die Funktion T als gewöhnliche Funktion der Komponenten q̇ µ der Geschwindigkeit betrachten,
diese Funktion partiell ableiten, und dann die Bahn q(t) und ihre Ableitung q̇(t) einsetzen. Dadurch wird
der Ausdruck ∂T /∂ q̇ µ zu einer Funktion der Zeit, die wir dann wieder nach t ableiten können.
Wir schreiben wie üblich die partiellen Ableitungen von Funktionen nach ihren Argumenten mit einem
geschwungenen ‘∂’. Dagegen ist die totale Zeitableitung ‘d/dt’ immer so zu verstehen, dass wir den
Ausdruck, auf den sie wirkt, entlang einer bestimmten Bahn q(t) auswerten, und diese Funktion dann
nach t ableiten. An dieser Stelle haben die Ableitungssymbole ‘∂’ und ‘d’ also wirklich unterschiedliche
Bedeutungen.
Da dies im folgenden sehr wichtig ist, machen wir es uns noch einmal dadurch klar, dass wir die Bewegungsgleichungen (11.29) etwas expliziter ausschreiben. Da die Funktion T und damit auch die Ableitungen ∂T /∂ q̇ µ nur indirekt über q̇ µ (t) von der Zeit t abhängen, gilt natürlich die Kettenregel, also
d ∂T ∂2T
∂ 2 T dq̇ ν
=
q̈ ν
=
dt ∂ q̇ µ
∂ q̇ µ ∂ q̇ ν dt
∂ q̇ µ ∂ q̇ ν
⇒
Mµν q̈ ν = Fµ .
(11.30)
Wenn T als quadratische Funktion durch eine Massenmatrix gegeben ist, ist die zweite Ableitung genau
diese Massenmatrix. Wir sehen, dass (11.29) nichts anderes ist als eine etwas ungewöhnliche Darstellung
der Newtonschen Bewegungsgleichungen, wonach Masse mal Beschleunigung gleich Kraft ist.
Es stellt sich daher die Frage, warum wir diese merkwürdige Formulierung überhaupt benutzen. Die Bewegungsgleichung (11.30) sieht doch viel einfacher aus. Sie stellt über die Massenmatrix eine Beziehung
zwischen der Kraft F ∈ T∗ Q und der Beschleunigung q̈ ∈ TQ her, und beschreibt so die Bewegungen des
Systems im Konfigurationsraum auf eine geometrische Art und Weise, die zudem noch unabhängig von der
Wahl der Koordinaten ist. Da alle drei beteiligten Objekte wie Tensoren transformieren, gilt die Gleichung
in jedem affinen Koordinatensystem. Das haben wir gerade verwendet, um die Bewegungsgleichungen für
einen zusammengesetzten harmonischen Oszillator zu entkoppeln
50
Um die Bewegungsgleichungen für ein gegebenes mechanisches System aufstellen und lösen zu können,
genügt das jedoch meistens nicht. Wir müssen auch krummlinige Koordinatensysteme verwenden. Das
Zentralkraftproblem, und insbesondere das Keplersche Problem der Planetenbahnen, konnten wir zum
Beispiel erst erfolgreich angehen, nachdem wir Kugelkoordinaten eingeführt hatten. In krummlinigen Koordinatensystem gilt jedoch die einfache Darstellung (11.30) der Bewegungsgleichungen nicht mehr.
Zwar können wir die Massenmatrix Mµν auch in einem krummlinigen Koordinatensystem darstellen,
wobei ihre Komponenten dann ortsabhängig werden. Um jedoch die Beschleunigung in krummlinigen
Koordinatensystemen darzustellen, benötigen wir eine kovariante Ableitung. Dies hatten wir in Kapitel 10
und insbesondere in Aufgabe 10.26 gesehen. Es genügt nicht, einfach die zweite Ableitung der Koordinatenfunktionen q µ (t) zu bilden.
Es stellt sich nun heraus, dass es sehr viel einfacher ist, die Gleichung (11.29) in ein krummliniges Koordinatensystem zu transformieren, als die scheinbar einfachere Gleichung (11.30). Wir müssen dazu noch
nicht einmal das Konzept der kovarianten Ableitung explizit verwenden, obwohl wir letztlich wieder eine
solche bilden werden. Zudem ist das Ergebnis so allgemein, dass wir von der kinetischen Energie noch
nicht einmal annehmen müssen, dass sie homogen vom Grad 2 ist, also quadratisch in den Geschwindigkeiten. Das wird sich später als nützlich erweisen, wenn wir sehr viel allgemeinere Bewegungsgleichungen
betrachten.
Das Ziel ist nun, die Bewegungsgleichung (11.29) in einem krummlinigen Koordinatensystem auf dem
Konfigurationsraum Q darzustellen. Dazu sei weiterhin {q µ } ein affines Koordinatensystem, in dem die
Gleichung in der angegebenen Form gelten soll. Die krummlinigen Koordinaten bezeichnen wir mit {q α }.
Oft nennt man diese auch verallgemeinerte oder generalisierte Koordinaten.
Die Unterscheidung zwischen den beiden Koordinatensystemen erfolgt, wie bisher auch, durch zwei
verschiedene Indexmengen. Für die affinen Koordinaten verwenden wir die Indizes µ, ν, . . ., für die verallgemeinerten Koordinaten die Indizes α, β, . . .. Für ein N -Teilchen-System können die Koordinaten q µ
zum Beispiel die kartesischen Ortskoordinaten {x1 , y1 , z1 , . . . , xN , yN , zN } der einzelnen Teilchen sein,
und als verallgemeinerte Koordinaten q α können wir die Darstellungen derselben Orte in Kugelkoordinaten {r1 , ϑ1 , ϕ1 , . . . , rN , ϑN , ϕN } verwenden.
Die Umrechnung zwischen den beiden Koordinatensystemen erfolgt dadurch, dass wir die affinen Koordinaten q µ als Funktionen der verallgemeinerten Koordinaten q α darstellen. Um ein möglichst allgemeines
Ergebnis zu bekommen, lassen wir sogar zu, dass diese Funktionen explizit von der Zeit abhängen. Mit
anderen Worten, wir können sogar zu jedem Zeitpunkt ein anderes krummliniges Koordinatensystem verwenden. Die Übergangsfunktionen haben dann die Form
(11.31)
q µ = q µ {q α }, t .
Nun betrachten wir eine Bahn q(t) des Systems im Konfigurationsraum. In krummlinigen Koordinaten
wird diese Bahn durch einen Satz von Funktionen q α (t) dargestellt. Folglich gilt für die Darstellung derselben Bahn in affinen Koordinaten
q µ (t) = q µ {q α (t)}, t .
(11.32)
Wenn wir diese Gleichung nach der Zeit ableiten, finden wir die affinen Komponenten q̇ µ (t) der Geschwindigkeit, ausgedrückt durch die verallgemeinerten Koordinaten q α (t) und deren Zeitableitungen q̇ α (t), den
verallgemeinerten Geschwindigkeiten. Auf der rechten Seite müssen wir dazu die partiellen Ableitungen
der affinen Koordinaten nach den krummlinigen Koordinaten bilden, und zusätzlich die partielle Ableitung
der Übergangsfunktionen nach der Zeit,
∂q µ
∂q µ
{q α (t)}, t .
(11.33)
q̇ µ (t) = α {q α (t)}, t q̇ α (t) +
∂q
∂t
Wir schreiben das etwas verkürzt in der Form
∂q µ
∂q µ
.
(11.34)
q̇ µ = α q̇ α +
∂q
∂t
51
Der erste Term beschreibt wie üblich die Transformation eines Vektors von einem Koordinatensystem in
ein anderes. Der zweite Term tritt auf, weil das krummlinige Koordinatensystem zusätzlich von der Zeit
abhängen kann. Wenn die Koordinaten q α (t) zeitlich konstant sind, so bedeutet das nämlich nicht, dass die
Teilchen ruhen, also die Konfiguration q(t) zeitlich konstant ist.
Nun können wir die kinetische Energie T als Funktion der neuen Koordinaten ausdrücken. Ursprünglich
war T ({q̇ µ }) eine Funktion, die nur von den Komponenten q̇ µ der Geschwindigkeit abhing. Da diese aber
nun über (11.34) sowohl von den verallgemeinerten Geschwindigkeiten q̇ α als auch von den verallgemeinerten Koordinaten q α und sogar der Zeit t abhängen, wird die kinetische Energie jetzt zu einer Funktion
T ({q α }, {q̇ α }, t).
Das ist letztlich nichts anderes als die weiter oben bereits gemachte Feststellung, dass die Massenmatrix
eines mechanischen Systems in krummlinigen Koordinaten ortsabhängig wird, da es sich um die Darstellung eines Tensors in einem krummlinigen Koordinatensystem handelt. Da dieses Koordinatensystem
zudem von der Zeit abhängt, ergibt sich zusätzlich noch eine Zeitabhängigkeit.
In krummlinigen Koordinaten hängt die kinetische Energie vom den Ortskoordinaten, den
Komponenten der Geschwindigkeit und explizit von der Zeit ab.
Am besten machen wir uns das wieder an einem Beispiel klar. Wir betrachten ein einzelnes Teilchen, das
sich frei im Raum bewegt. Als affine Koordinaten q µ verwenden wir (x, y, z), und als verallgemeinerte
Koordinaten q α , um auch eine explizite Zeitabhängigkeit zu bekommen, rotierende Zylinderkoordinaten
(r, ϕ, z). Die zeitabhängigen Übergangsfunktionen (11.31) sollen explizit durch
x = r cos(ϕ − ω t),
y = r sin(ϕ − ω t)
(11.35)
gegeben sein. Die Winkelgeschwindigkeit ω gibt an, wie schnell sich das Koordinatensystem dreht. Die
Koordinate z bleibt einfach unverändert. Sie spielt in den folgenden Überlegungen keine Rolle. Wenn wir
diese Gleichungen nach der Zeit t ableiten, finden wir
ẋ = ṙ cos(ϕ − ω t) − (ϕ̇ − ω) r sin(ϕ − ω t),
ẏ = ṙ sin(ϕ − ω t) + (ϕ̇ − ω) r cos(ϕ − ω t).
(11.36)
Das sind die explizit ausgeschriebenen Gleichungen (11.34) für dieses spezielle Beispiel. Die rechten
Seiten hängen nicht nur von den verallgemeinerten Geschwindigkeiten (ṙ, ϕ̇) ab, sondern auch von den
Koordinaten (r, ϕ) und sogar explizit von der Zeit t. Für die kinetische Energie ergibt sich
T =
1
1
m (ẋ2 + ẏ 2 + ż 2 ) = m (ṙ 2 + r 2 (ϕ̇ − ω)2 + ż 2 ).
2
2
(11.37)
Auch diese Funktion ist wieder quadratisch in den verallgemeinerten Geschwindigkeiten, aber sie hängt
zusätzlich von r ab, und sie enthält auch noch Terme, die proportional zu ω und ω 2 sind. Das ist auch
klar, denn die kinetische Energie eines Teilchens, dass in diesem Koordinatensystem “ruht”, kreist ja in
Wirklichkeit mit der Winkelgeschwindigkeit ω um den Ursprung.
Aufgabe 11.11 In welcher konkreten physikalischen Situation w ürde die Wahl eines solchen Koordinatensystems nahe liegen?
Aufgabe 11.12 Man ersetze in (11.35) ω t durch eine beliebige Funktion γ(t) und zeige, dass sich dann
auch eine explizit zeitabhängige Energiefunktion T ergibt.
52
Die d’Alembertschen Gleichungen
Wir wollen nun die Bewegungsgleichungen in krummlinigen Koordinaten darstellen. Da die kinetische
Energie T ursprünglich nur eine Funktion der Geschwindigkeiten q̇ µ war, können wir die partiellen Ableitungen von T nach q α und q̇ α durch die Ableitungen der ursprünglichen Funktion T nach q̇ µ ausdrücken.
Mit Hilfe der Kettenregel finden wir
∂T
∂T ∂ q̇ µ
∂T ∂q µ
=
=
.
∂ q̇ α
∂ q̇ µ ∂ q̇ α
∂ q̇ µ ∂q α
(11.38)
Hier haben wir verwendet, dass aus (11.34) ∂ q̇ µ /∂ q̇ α = ∂q µ /∂q α folgt.
Die partiellen Ableitungen ∂q µ /∂q α , die in (11.38) vorkommen, sind die ortsabhängigen Übergangsmatrizen für die Koordinatentransformation von {q µ } nach {q α }. Wir haben also gezeigt, dass sich die
partiellen Ableitungen pα = ∂T /∂ q̇ α bzw. pµ = ∂T /∂ q̇ µ bei einer Koordinatentransformation wie die
Komponenten eines dualen Vektors verhalten. Dies ist natürlich der Impulsvektor p ∈ T ∗ Q des Systems.
Seine Komponenten pα bezüglich des krummlinigen Koordinatensystems werden auch als verallgemeinerte Impulse bezeichnet.
Die entsprechende Rechnung für die partiellen Ableitungen von T nach den Koordinaten q α ist etwas
komplizierter, da wir dazu die rechte Seite von (11.34) nochmal nach q α ableiten müssen. Das ergibt
∂T ∂ q̇ µ
∂T ∂ 2 q µ β
∂T
∂2qµ = µ α = µ
q̇ + α
.
∂q α
∂ q̇ ∂q
∂ q̇
∂q ∂t
∂q α ∂q β
(11.39)
Wir wollen nun versuchen, die linke Seite der Gleichung (11.29) durch die krummlinigen Koordinaten
auszudrücken. Als Ansatz bietet sich dazu an, die Zeitableitung von (11.38) zu bilden,
d ∂T
d ∂T ∂q µ d ∂T ∂q µ
∂T d ∂q µ =
+
=
.
dt ∂ q̇ α
dt ∂ q̇ µ ∂q α
dt ∂ q̇ µ ∂q α ∂ q̇ µ dt ∂q α
(11.40)
Auch das ist natürlich wieder so zu verstehen, dass wir zuerst die partiellen Ableitungen bilden, dann eine
Bahn q(t) einsetzen, die wir jetzt wahlweise durch die Koordinatenfunktionen q µ (t) oder q α (t) darstellen
können, und anschließend die totalen Zeitableitungen d/dt bilden.
Der erste Term in der Klammer ist genau der, den wir suchen, nämlich die linke Seite von (11.29). Um
den zweiten Term weiter umzuformen, benutzen wir, dass die affinen Koordinaten q µ sowohl implizit über
die krummlinigen Koordinaten als auch explizit von der Zeit abhängen. Daher gilt
∂2qµ
∂2 qµ β
d ∂q µ
= α β q̇ + α .
dt ∂q α
∂q ∂t
∂q ∂q
(11.41)
Das ist aber genau der Ausdruck in der Klammer in (11.39). Wir finden also
d ∂T ∂q µ
∂T
d ∂T
−
=
.
dt ∂ q̇ α ∂q α
dt ∂ q̇ µ ∂q α
(11.42)
Um das für die Bewegungsgleichung zu verwenden, multiplizieren wir diese mit der Übergangsmatrix
∂q µ /∂q α und setzen
∂q µ
Fα = α Fµ .
(11.43)
∂q
Die Größen Fα werden als verallgemeinerte Kräfte bezeichnet. Es sind die Komponenten des Kraftvektors
F ∈ T∗ Q, dargestellt in den krummlinigen Koordinaten. Die Gleichung (11.43) beschreibt wieder das
Transformationsverhalten eines dualen Vektors unter einer Koordinatentransformation.
53
Wenn wir nun dies und (11.42) in die Bewegungsgleichung (11.29) einsetzen, so lassen sich diese
schließlich wie folgt schreiben,
∂T
d ∂T
d’Alembertsche
= Fα .
(11.44)
α −
Bewegungsgleichung
dt ∂ q̇
∂q α
Die in dieser Form dargestellten Bewegungsgleichungen für ein mechanisches System heißen
d’Alembertsche Gleichungen. Bis auf den zusätzlichen Term auf der linken Seite, der die Abhängigkeit
der kinetischen Energie von den Koordinaten berücksichtigt, haben sie die gleiche Form wie vorher die
Gleichungen (11.29) in affinen Koordinaten. Und es gibt natürlich wieder eine reelle Gleichung für jeden
Freiheitsgrad des Systems.
Tatsächlich verschwindet der zusätzliche Term auf der linken Seite, wenn der Zusammenhang zwischen
q µ und q α affin und zeitunabhängig ist. Dann sind die neuen Geschwindigkeiten q̇ α lineare Funktionen der
alten Geschwindigkeiten q̇ µ , und somit hängt auch die kinetische Energie nur von q̇ α , aber nicht von q α
ab. Die allgemeinere Form (11.44) gilt also auch für affine Koordinatensysteme.
Um die Bewegungsgleichungen für ein spezielles mechanisches System auf diese Form zu bringen,
müssen wir nur zwei Dinge tun. Wir müssen die kinetische Energie T als Funktion der verallgemeinerten
Koordinaten und deren Zeitableitungen darstellen, und wir müssen dasselbe mit der Kraft F tun. Bei der
Kraft müssen wir zusätzlich beachten, dass es sich dabei um einen dualen Vektor handelt. Wir müssen
deshalb gemäß (11.43) den Index transformieren.
Um an unserem Beispiel von oben zu demonstrieren, dass die d’Alembertschen Gleichungen tatsächlich
die richtigen Bewegungsgleichungen sind, setzen wir für T die Funktion (11.37) ein. Die Kraft soll der
Einfachheit halber verschwinden, und wir setzen auch ω = 0. Das Zylinderkoordinatensystem soll also
nicht rotieren. Dann ergeben sich nach einer kurzen Rechnung die folgenden Bewegungsgleichungen
d
dt
d
dt
∂T
∂T
d
−
=
m ṙ − m r ϕ̇2 = 0,
∂ ṙ
∂r
dt
∂T
∂T
d
d ∂T
∂T
d
−
=
m r 2 ϕ̇ = 0,
−
=
m ż = 0.
∂ ϕ̇
∂ϕ
dt
dt ∂ ż
∂z
dt
(11.45)
Das bemerkenswerte an diesem Beispiel ist, dass die beiden letzten Gleichungen ganz automatisch die entscheidenden Erhaltungssätze liefern, die wir benutzen können, um die Bewegungsgleichungen zu lösen.
Es ist nämlich m ż = pz die Impulskomponente in z-Richtung, und pϕ = m r 2 ϕ̇ der Drehimpuls um die
z-Achse. Beides sind natürlich für ein kräftefreies Teilchen Erhaltungsgrößen.
Ebenfalls bemerkenswert ist, dass die Komponente pϕ = ∂T /∂ ϕ̇ des Impulses nach unserer neuen,
allgemeinen Definition, wonach der Impuls die Ableitung der Energie nach der Geschwindigkeit ist, gerade
der Drehimpuls ist, der einer Rotation in Richtung der Koordinaten ϕ entspricht. Anscheinend passt sich
der Begriff “Drehimpuls” sehr gut in dieses allgemeine Konzept ein. Darauf werden wir später aber noch
im Detail eingehen.
Aufgabe 11.13 Man finde die allgemeine Lösung der Bewegungsgleichungen (11.45) und zeige, dass sich
in dem dargestellten Beispiel auch für ω 6= 0 aus den d’Alembertschen Gleichungen die richtigen Bewegungsgleichungen für ein freies Teilchen ergeben.
Aufgabe 11.14 Welche physikalischen Dimensionen haben die verallgemeinerten Koordinaten (r, ϕ, z) in
dem gezeigten Beispiel? Welche physikalischen Dimensionen haben folglich die verallgemeinerten Impulse
(pr , pϕ , pz ) und Kräfte (Fr , Fϕ , Fz ), wenn diese nicht gleich Null gesetzt sind?
Aufgabe 11.15 Die kinetische Energie T sei eine homogene quadratische Funktion der verallgemeinerten
Geschwindigkeiten q̇ α . Sie hänge nicht explizit von t, aber in irgendeiner Weise von den verallgemeinerten Koordinaten q α ab. Man zeige, dass dann die zeitliche Änderung der kinetischen Energie durch die
54
mechanische Leistung gegeben ist, die sich als Produkt von Kraft und Geschwindigkeit ergibt,
dT
= F · q̇ = Fµ q̇ µ = Fα q̇ α .
dt
(11.46)
Warum kann die rechte Seite dieser Gleichung in jedem beliebigen Koordinatensystem ausgewertet werden?
Aufgabe 11.16 Man zeige, dass sich die linke Seite der d’Alembertschen Gleichung wie ein dualer Vektor
transformiert, und zwar beim Übergang von einem beliebigen krummlinigen Koordinatensystem zu einem
beliebigen anderen. Man führe dazu einen zweiten Satz von krummlinigen Koordinaten q µ ein, stelle diese
als Funktionen von q α dar, und zeige
d ∂T
∂T
∂q µ d ∂T
∂T .
(11.47)
−
=
−
dt ∂ q̇ α ∂q α
∂q α dt ∂ q̇ µ ∂q µ
Die gerade durchgeführte Herleitung, bei der die Koordinaten q µ affin waren, ist also nur ein Spezialfall
von diesem allgemeinen Transformationsverhalten.
Die Lagrange-Funktion
Besonders einfach ist die Situation dann, wenn alle auftretenden Kräfte Potenzialkräfte sind. Dann ist
nämlich die Kraft der Gradient des Potenzials, und dann gilt natürlich in jedem Koordinatensystem, dass
die Komponenten dieses dualen Vektors durch die partiellen Ableitungen nach den Koordinaten gegeben
sind. Explizit,
∂V
∂q µ
∂q µ ∂V
∂V
Fµ = − µ ⇒ F α = α Fµ = − α µ = − α .
(11.48)
∂q
∂q
∂q ∂q
∂q
Das Potenzial kann dabei auch von t abhängen, und die Umrechnungsformel (11.48) gilt auch dann, wenn
die verallgemeinerten Koordinaten q α aus q µ durch eine zeitabhängige Transformation auseinander hervor
gehen. In diesem Fall sind die Übergangsmatrizen ∂q µ /∂q α zwar zeitabhängig, aber die Beziehung (11.48)
gilt immer noch zu jedem Zeitpunkt.
Die d’Alembertschen Bewegungsgleichungen lauten jetzt
∂T
∂V
d ∂T
= 0.
α −
α +
dt ∂ q̇
∂q
∂q α
(11.49)
Da das Potenzial V nicht von der Geschwindigkeit abhängt, lässt sich das sogar noch einfacher schreiben.
Wir definieren eine Funktion
LagrangeFunktion
L = T − V,
(11.50)
die auch wieder vom Ort, der Geschwindigkeit und eventuell explizit von der Zeit abhängt. Diese Funktion
heißt Lagrange-Funktion.
Die Lagrange-Funktion ist die Differenz von kinetischer und potenzieller Energie.
Mit dieser Funktion können die d’Alembertschen Bewegungsgleichungen in einer sehr kompakten Form
geschrieben werden, nämlich
d ∂L
∂L
Lagrange−
= 0.
(11.51)
α
Gleichung
dt ∂ q̇
∂q α
Die gesamte Dynamik eines mechanischen System wird somit durch eine einzige Funktion L auf dem
Konfigurationsraum beschrieben. Diese Funktion können wir in einem beliebigen Koordinatensystem darstellen, so dass die Lagrange-Gleichung (11.51) auch in jedem beliebigen Koordinatensystem ausgewertet
55
werden kann. Auch hier ergibt sich natürlich wieder eine reelle Differenzialgleichung für jeden Freiheitsgrad, also für jeden Wert, den der Index α annehmen kann.
Für die explizite Herleitung von Bewegungsgleichungen für mechanische System ist die LagrangeFunktion ein sehr effizientes Werkzeug. Wir wollen das am Beispiel des allgemeinen Zentralkraftproblems
demonstrieren. Ein Teilchen der Masse m befinde sich in einem Potenzial V = V (r). Seine kinetische
Energie, in Kugelkoordinaten ausgedrückt, ist
T =
1
m ṙ 2 + r 2 ϑ̇2 + r 2 sin2 ϑ ϕ̇2 .
2
(11.52)
Aufgabe 11.17 Wieso ergibt sich dieser Ausdruck unmittelbar aus der Darstellung (10.54) der Euklidischen Metrik in Kugelkoordinaten?
Die Lagrange-Funktion für dieses System ist folglich
L=T −V =
1
m ṙ 2 + r 2 ϑ̇2 + r 2 sin2 ϑ ϕ̇2 − V (r).
2
(11.53)
Diese Funktion müssen wir jetzt nur noch in (11.51) einsetzen und die entsprechenden partiellen Ableitungen bilden, um die Bewegungsgleichungen zu bekommen,
d
∂L ∂L
m ṙ − m r ϑ̇2 − m r sin2 ϑ ϕ̇2 + V 0 (r) = 0,
−
=
∂ ṙ
∂r
dt
d
∂L ∂L
m r 2 ϑ̇ − m r 2 sin ϑ cos ϑ ϕ̇2 = 0
−
=
∂ϑ
dt
∂ ϑ̇
d ∂L ∂L
d
m r 2 sin2 ϑ ϕ̇ = 0.
−
=
dt ∂ ϕ̇ ∂ϕ
dt
d
dt
d
dt
(11.54)
Aus der zweiten Gleichung entnehmen wir, dass diese für ϑ(t) = π/2 erfüllt ist. Es ist also möglich, dass
sich das Teilchen nur in der Äquatorebene aufhält. Tatsächlich genügt es dazu, die Anfangsbedingungen
ϑ(t0 ) = π/2 und ϑ̇(t0 ) = 0 zu wählen. Die erste und die dritte Gleichung vereinfachen sich dann zu
d
m ṙ − m r ϕ̇2 + V 0 (r) = 0,
dt
d
m r 2 ϕ̇ = 0.
dt
(11.55)
Wir finden wieder die Drehimpulserhaltung pϕ = m r 2 ϕ̇ = konst, und für die radiale Bewegungsgleichung können wir ein effektives Potenzial einführen,
m r̈ = −Ve 0 (r),
pϕ2
mit Ve (r) = V (r) +
.
2 m r2
(11.56)
Was wir in Kapitel 8 erst durch mühsames Umrechnen der Koordinaten herleiten mussten, ergibt sich hier
ohne größeren Aufwand, indem wir einfach die Lagrange-Funktion in Kugelkoordinaten darstellen.
Natürlich haben wir dafür schon ein wenig Vorarbeit geleistet, indem wir zum Beispiel die Euklidische
Metrik in Kugelkoordinaten dargestellt haben, so dass wir dies in (11.52) verwenden konnten. Trotzdem
ist die Herleitung jetzt sehr viel einfacher. Denn wir haben hier nicht nur, wie in Kapitel 8, die Bewegungsgleichungen für ein Teilchen in der Äquatorebene bekommen, sondern mit (11.54) auch die für ein
Teilchen, das sich beliebig im Raum bewegt und eine nicht verschwindende Geschwindigkeit ϑ̇ hat. Das
wäre mit den Methoden in Kapitel 8 ungleich schwieriger gewesen.
Aufgabe 11.18 Man zeige, dass der Ausdruck für pϕ = m r 2 sin2 ϑ ϕ̇ in der letzten Gleichung in (11.54)
auch für ϑ 6= π/2 die z-Komponente des Drehimpulses des Teilchens ist.
56
Aufgabe 11.19 Am Beispiel des gekoppelten harmonischen Oszillators von weiter oben, und auch schon
früher in Kapitel 6, hatten wir gesehen, dass eine nützlich Strategie zur Lösung von Bewegungsgleichungen
deren Entkoppelung ist. Man beweise folgenden allgemeinen Satz. L ässt sich die Lagrange-Funktion eines
mechanischen Systems als Summe von zwei Funktionen L = L1 + L2 schreiben, wobei L1 nur von einem
Teil der Koordinaten abhängt, und L2 nur von den übrigen Koordinaten, so sind die beiden Sätze von
Bewegungsgleichungen unabhängig voneinander. Sie können unabhängig voneinander gelöst werden, so
als würde es sich um zwei voneinander getrennte mechanische System handeln.
Aufgabe 11.20 Man wende den Satz aus Aufgabe 11.19 auf ein System von zwei Teilchen an, die sich
frei im dreidimensionalen Raum bewegen und durch die Gravitationskraft anziehen. Welches sind hier
die am besten geeigneten verallgemeinerten Koordinaten, in denen die Lagrange-Funktion sogar in vier
unabhängige Summanden zerfällt?
Kräfte und Potenziale
Die d’Alembertsche Formulierung der Bewegungsgleichungen können wir für jedes mechanische System
verwenden. Wir müssen nur, wenn wir ein krummliniges oder sogar zeitabhängiges Koordinatensystem
verwenden, die Komponenten der Kräfte entsprechend in die verallgemeinerten Kräfte umrechnen. Wir
können dies tun, indem wir direkt die Teilchenkoordinaten r n,i bzw. die Teilchenorte rn im dreidimensionalen Raum als Funktionen der krummlinigen Koordinaten q α auf dem Konfigurationsraum darstellen,
also
rn,i = rn,i {q α }, t
bzw. rn = rn {q α }, t .
(11.57)
Hier ist n wieder der Teilchenindex, und i der Index für ein kartesisches Koordinatensystem im dreidimensionalen Raum. Die verallgemeinerten Kräfte Fα ergeben sich dann aus der allgemeinen Formel (11.43),
wobei wir die Summe über den Index µ aufspalten müssen in eine Summe über die Teilchen n und eine
Summe über die Vektorkomponenten i. Das ergibt
Fα =
X ∂rn,i
n
∂q α
Fn,i =
X ∂rn
n
∂q α
· Fn .
(11.58)
Die Summe über den Vektorindex i können wir auch wieder als Skalarprodukt im Euklidischen Raum
schreiben. In dieser Form lassen sich die verallgemeinerten Kräfte oft am einfachsten berechnen.
Als Beispiel betrachten wir eine Reibungskraft als typisches Beispiel für eine Kraft, die sich nicht aus
einem Potenzial ableiten lässt. Das System bestehe aus nur einem Teilchen, und wir benutzen Zylinderkoordinaten (r, ϕ, z). Der Ort des Teilchens ist dann
r = o + r cos ϕ ex + +r sin ϕ ey , +z ez ,
(11.59)
wobei (ex , ey , ez ) eine Orthonormalbasis ist. Die kinetische Energie entnehmen wir aus (11.37), indem
wir dort ω = 0 setzen,
1
T = m (ṙ 2 + r 2 ϕ̇2 + ż 2 ).
(11.60)
2
Von der Kraft nehmen an, dass es sich um eine lineare Reibungskraft handelt. Sie soll proportional zur
Geschwindigkeit und ihr entgegengerichtet sein,
F = −η ṙ
⇒
Fα =
∂r
∂r
∂r ∂r β
q̇ .
·
α · F = −η
α · ṙ = −η
∂q
∂q
∂q α ∂q β
(11.61)
Die Summe über n in (11.58) ist hier trivial, da nur ein Teilchen vorhanden ist. Der letzte Ausdruck
ergibt sich, indem wir die Geschwindigkeit ṙ mit Hilfe der Kettenregel als Funktion der verallgemeinerten
57
Geschwindigkeiten q̇ α ausdrücken. Die Skalarprodukte
gαβ =
∂r ∂r
∂ri ∂ri
∂ri ∂rj
= α β = α β δij
α ·
β
∂q ∂q
∂q ∂q
∂q ∂q
(11.62)
für α, β ∈ {r, ϕ, z} haben wir bereits einmal ausgerechnet. Das sind nämlich die Komponenten der Metrik
in Zylinderkoordinaten, die in kartesischen Koordinaten durch g ij = δij dargestellt wird. Mit (10.49), um
die Koordinate z ergänzt, ergibt sich
grr = 1,
gϕϕ = r 2 ,
gzz = 1,
(11.63)
und alle anderen Komponenten sind gleich Null. Im Falle eines Ein-Teilchen-Systems wird auf diese Weise
natürlich auch auf dem Konfigurationsraum eine Metrik definiert, und diese können wir in beliebigen
krummlinigen Koordinatensystemen darstellen. Für die verallgemeinerten Kräfte ergibt sich daraus
Fα = −η gαβ q̇ β
⇒
Fr = −η ṙ,
Fϕ = −η r 2 ϕ̇,
Fz = −η ż.
(11.64)
Die verallgemeinerten Kräfte sind nicht einfach proportional zu den verallgemeinerten Geschwindigkeiten, sondern es tritt bei der ϕ-Komponente eine ortsabhängige Proportionalitätskonstante auf. Dafür gibt
es wieder eine einfache geometrische Erklärung. Die Kraft ist ein dualer Vektor, die Geschwindigkeit dagegen ein Vektor. Deshalb wird der Zusammenhang zwischen den beiden durch die Metrik hergestellt, und
deren Komponenten sind in krummlinigen Koordinaten ortsabhängig.
Die linke Seite der d’Alembertschen Gleichung hatten wir bereits in (11.45) ausgerechnet. Auf der
rechten Seite steht jetzt die Kraft (11.64). Folglich ergeben sich für das Teilchen mit linearer Reibung die
Bewegungsgleichungen
d
m ṙ = m r ϕ̇2 − η ṙ,
dt
d
m r 2 ϕ̇ = −η r 2 ϕ̇,
dt
d
m ż) = −η ż.
dt
(11.65)
Aufgabe 11.21 Man gebe die Lösung dieser Bewegungsgleichungen mit den Anfangsbedingungen
r(0) = ρ,
ṙ(0) = 0,
ϕ(0) = 0,
ϕ̇(0) = ω,
z(0) = 0,
ż(0) = v
(11.66)
an. Der Trick besteht auch hier darin, zuerst die Bewegungsgleichungen f ür den Drehimpuls pϕ = m r 2 ϕ̇
zu lösen. Es handelt sich zwar jetzt nicht mehr um eine Erhaltungsgr öße, aber sie lässt sich dennoch lösen,
und danach entkoppeln die übrigen Bewegungsgleichungen.
Aufgabe 11.22 Man führe die gleiche Rechnung in Kugelkoordinaten aus. Welche verallgemeinerten
Komponenten (Fr , Fϑ , Fϕ ) ergeben sich in diesem Fall für die die Reibungskraft?
Natürlich sind Zylinder- oder Kugelkoordinaten in diesem Fall nicht die am besten an das Problem angepassten Koordinaten. Die Bewegungsgleichungen in kartesischen Koordinaten sind viel einfacher, da sie
für eine lineare Reibungskraft unmittelbar entkoppeln. Wir können aber eine kleine Variation an diesem
Problem vornehmen, so dass das nicht mehr der Fall ist.
Das leicht veränderte Problem dient gleichzeitig als Beispiel für eine verallgemeinerte Form der Bewegungsgleichungen, die sich als Kombination der d’Alembertschen und Lagrangeschen Form ergibt.
Da Kräfte additiv sind, können wir sie in konservative Kräfte und solche Kräfte zerlegen, die sich nicht
aus einem Potenzial ableiten lassen. Wir fassen dann alle konservativen Kräfte zu einem Potenzial V
zusammen und definieren wie üblich eine Lagrange-Funktion L = T − V. Dann müssen wir aber die
nicht-konservativen Kräfte noch zusätzlich in die Bewegungsgleichungen aufnehmen, indem wir ihre verallgemeinerten Komponenten Fα auf die rechte Seite schreiben.
58
Als Kombination der Bewegungsgleichungen (11.44) und (11.51) ergibt sich dann
allgemeine
Bewegungsgleichung
∂L
d ∂L
= Fα .
α −
dt ∂ q̇
∂q α
(11.67)
Für V = 0 ist L = T , und es ergibt sich wieder die d’Alembertsche Formulierung. Für F α = 0 sind alle
Kräfte konservativ, und es ergibt sich die Lagrangesche Formulierung.
Als Beispiel fügen wir zu unserem oben definierten Teilchen mit Reibungskraft ein Potenzial V = V (r)
hinzu, das nur vom Abstand von der z-Achse abhängen soll. In diesem Fall sind die Zylinderkoordinaten
etwas besser an das Problem angepasst, denn dann hängt das Potenzial nur von einer Koordinate ab. Wir
können uns als Realisierung eines solchen Systems ein elektrisch geladenes Teilchen vorstellen, das sich
in einem Medium, das eine Reibung verursacht, in der Nähe eines geladenen Drahtes befindet.
Um die Bewegungsgleichungen in der Form (11.67) aufzuschreiben, müssen wir nur statt der kinetischen Energie (11.60) die Lagrange-Funktion
L=T −V =
1
m ṙ 2 + r 2 ϕ̇2 + ż 2 − V (r)
2
(11.68)
verwenden. Die Reibungskraft ist die gleiche wie vorher. Folglich ändert sich nur die Bewegungsgleichung
für die Koordinate r, denn nur in sie geht die Ableitung des Potenzials ein. Es genügt außerdem, nur die
Bewegungsgleichungen für r und ϕ zu betrachten, da die Bewegung in z-Richtung ohnehin entkoppelt,
d
m ṙ = m r ϕ̇2 − η ṙ − V 0 (r),
dt
d
m r 2 ϕ̇ = −η r 2 ϕ̇.
dt
(11.69)
Aufgabe 11.23 Das Potenzial sei V (r) = κ r 2 /2, bewirke also eine lineare, rücktriebende Kraft. Welche
Lösung ergibt sich dann aus den Anfangsbedingungen (11.66)? Auch hier l ässt sie sich wieder bestimmen,
wenn man zuerst die unveränderte Bewegungsgleichung für den Drehimpuls pϕ = m r 2 ϕ̇ löst.
Aufgabe 11.24 Es sei V (r) irgendeine monoton wachsende Funktion, so dass das Minimum des Potenzials auf der z-Achse liegt. Man zeige, dass in diesem Fall jede Bewegung, unabh ängig von den Anfangsbedingungen, früher oder später in der Nähe der z-Achse endet. Es gilt also r(t) → 0 für t → ∞.
Aufgabe 11.25 Man führe wieder die analogen Überlegungen in Kugelkoordinaten durch, wobei das Potenzial in diesem Fall kugelsymmetrisch sein soll. Man zeige entsprechend, dass bei einem monoton ansteigenden Potenzial V (r) das Teilchen stets in der Nähe des Ursprungs endet, also auch hier r(t) → 0
für t → ∞ gilt.
Die Lorentz-Kraft
Mit der Mischform (11.67) haben wir die allgemeinste Darstellung für die Bewegungsgleichungen eines mechanischen Systems in einem beliebigen krummlinigen Koordinatensystem angegeben. Wir wollen
jetzt noch der Frage nachgehen, was das allgemeinste Kraftgesetz ist, das sich allein aus einer LagrangeFunktion ableiten lässt. Bisher hatten wir argumentiert, dass es dazu ein Potenzial V geben muss, also eine
Funktion des Ortes q ∈ Q, deren Gradient die Kraft ist.
Eine genauere Betrachtung zeigt jedoch, dass sich eine viel größere Klasse von Kräfte durch eine
Lagrange-Funktion beschreiben lässt. Interessanterweise sind es genau diejenigen Kräfte, die wir als elektromagnetische Kräfte kennen. Das ist ein sehr bemerkenswerter Umstand, denn es zeigt, dass es offenbar
einen Zusammenhang zwischen der Lagrangeschen Formulierung der Mechanik und anderen, fundamentalen physikalischen Theorien gibt.
59
Um herauszufinden, welche Arten von Kräften sich prinzipiell aus einer Lagrange-Funktion ableiten
lassen, betrachten wir irgendeine Funktion L, die ein Polynom vom Grad 2 in den Geschwindigkeiten ist,
aber ansonsten beliebig vom Ort und der Zeit abhängt. Das ist natürlich noch längst nicht die allgemeinste mögliche Lagrange-Funktion. Da aber für mechanische Systeme die kinetische Energie immer eine
quadratische Funktion der Geschwindigkeit ist, treten nur solche Lagrange-Funktionen für physikalisch
realistische Systeme auf.
Wir sind außerdem bescheiden und betrachten nur ein einzelnes Teilchen, also einen dreidimensionalen Konfigurationsraum, dessen Koordinaten wir mit ri bezeichnen. Dies seien die üblichen kartesischen
Koordinaten im Euklidischen Raum, so dass wir alle Indizes nach unten schreiben können. Die LagrangeFunktion lautet dann
1
(11.70)
L = Mij (r, t) ṙi ṙj + Ai (r, t) ṙi − φ(r, t),
2
wobei Mij ein beliebiges symmetrisches Tensorfeld zweiter Stufe ist, Ai ein beliebiges Vektorfeld, und
φ ein beliebiges skalares Feld, jeweils auf dem dreidimensionalen Euklidischen Raum. Alle drei Felder
können zudem von der Zeit abhängen. Das ist offenbar die allgemeinste Funktion L mit den verlangen
Eigenschaften. Der spezielle Fall eines gewöhnlichen Teilchens der Masse m in einem Potenzial V (r, t)
ist darin enthalten. In diesem Fall müssen wir nur Mij (r, t) = m δij , Ai (r, t) = 0 und φ(r, t) = V (r, t)
setzen.
Wie lauten nun die Bewegungsgleichungen, die sich aus (11.70) ergeben? Wir müssen dazu nur die
Gleichung (11.51) auswerten. Zunächst ist
∂L
= Mkj (r, t) ṙj + Ak (r, t).
∂ ṙk
(11.71)
Diese Größe müssen wir nach der Zeit ableiten, wobei wir jetzt beachten müssen, dass wir zuerst für r
eine Bahn r(t) einsetzen müssen, und dass wir zusätzlich die explizite Zeitabhängigkeit der Felder M ij
und Ai berücksichtigen müssen. Es genügt, den Ausdruck wie folgt teilweise mit Hilfe der Kettenregel
auszuwerten,
d
d ∂L
Mkj (r, t) ṙj + ∂i Ak (r, t) ṙi + ∂t Ak (r, t).
(11.72)
=
dt ∂ ṙk
dt
Als Abkürzungen haben wir hier ∂t für die partielle Ableitung ∂/∂t nach der Zeit verwendet, und wie
üblich ist ∂i die Ableitung ∂/∂ri nach den räumlichen Koordinaten.
Jetzt müssen wir noch den zweiten Term in der Bewegungsgleichung ausrechnen. Das ergibt
∂L
1
= ∂k Mij (r, t) ṙi ṙj + ∂k Ai (r, t) ṙi − ∂k φ(r, t).
∂rk
2
(11.73)
Wenn wir die Terme dann noch ein wenig ordnen, bekommen wir die Lagrange-Gleichung
1
d
Mkj ṙj − ∂k Mij ṙi ṙj = ∂k Ai − ∂i Ak ṙi − ∂k φ + ∂t Ak .
dt
2
(11.74)
Diese Gleichung können wir wie folgt interpretieren. Auf der linken Seite steht die Zeitableitung des Impulses. Allerdings hängt der Impuls jetzt nicht mehr einfach nur linear mit der Geschwindigkeit zusammen,
sondern über eine orts- und zeitabhängige Massenmatrix Mij .
Das ist etwas ungewöhnlich, aber zumindest im Prinzip können wir uns ja durchaus vorstellen, dass
die Trägheit eines Teilchens keine feste Eigenschaft des Teilchen ist, sondern von Ort, Zeit und sogar der
Bewegungsrichtung im Raum abhängt. Genau dies wird durch die orts- und zeitabhängige Massenmatrix
Mij ausgedrückt, also durch den quadratischen Teil der Lagrange-Funktion. Der zusätzliche Term auf der
linken Seite ist derselbe, der sich auch in einem krummlinigen Koordinatensystem ergibt, wenn dort die
Massenmatrix ortsabhängig ist.
60
Da die Kraft auf der rechten Seite der interessantere Aspekt der Bewegungsgleichung ist, setzen wir von
nun an Mij = m δij , betrachten also ein “gewöhnliches” Teilchen mit der Masse m. Auf der linken Seite
der Bewegungsgleichung (11.74) steht dann m r̈k , also Masse mal Beschleunigung. Die Kraft Fk auf der
rechten Seite hängt aber immer noch vom Ort, der Geschwindigkeit und von der Zeit ab. Es ist also nicht
einfach eine Potenzialkraft. Eine kurze Rechnung zeigt, dass wir diese speziele Form einer Kraft bereits
kennen. Definieren wir nämlich zwei neue Vektorfelder,
Bi = εijk ∂j Ak
und Ei = ∂i φ + ∂t Ai ,
(11.75)
dann gilt für die Kraft auf der rechten Seite von (11.74)
Fk = εkij ṙi Bj + Ek
oder
F = ṙ × B + E.
(11.76)
Das ist die elektromagnetische Lorentz-Kraft. Nur die Ladungen und, je nach Wahl des Einheitensystems,
die Lichtgeschwindigkeit fehlt in dieser Darstellung. Das lässt sich aber leicht beheben. Hat das Teilchen
eine Masse m und eine Ladung q, und verwenden wir das Gaußsche Maßsystem, so müssen wir die
Lagrange-Funktion
1
q
L = m ṙ · ṙ + A(r, t) · ṙ − q φ(r, t)
(11.77)
2
c
verwenden, um die Bewegungsgleichung mit den richtigen Konstanten zu bekommen, nämlich
m r̈ =
q
ṙ × B + q E,
c
mit B = ∇ × A,
E = −∇φ −
1
∂t A.
c
(11.78)
Bemerkenswert an diesem Ergebnis ist nicht nur, dass die Lorentz-Kraft offenbar die allgemeinste Form
einer Kraft ist, die sich für ein einzelnes Teilchen aus einer Lagrange-Funktion ableiten lässt. Das eigentlich verblüffende ist, dass nur solche elektrische und magnetische Felder auftreten, die Lösungen der
homogenen Maxwell-Gleichungen sind, für die also gilt
∇×E+
1
∂t B = 0,
c
∇ · B = 0.
(11.79)
Denn genau diese Felder lassen sich durch ein elektrisches Potenzial φ und ein magnetisches Vektorpotenzial A wie in (11.78) darstellen.
Es lassen sich also nicht nur Potenzialkräfte aus einer Lagrange-Funktion ableiten, sondern auch geschwindigkeitsabhängige Kräfte, wenn sie die Form der Lorentz-Kraft haben. Dass dem so ist, können
wir an dieser Stelle nur feststellen. Dass es sich dabei um eine sehr tiefsinnige Erkenntnis handelt, wird
erst sehr viel später klar werden, wenn wir nämlich zeigen, dass sich auch die Bewegungsgleichungen des
elektromagnetischen Feldes, also die Maxwell-Gleichungen aus einer Lagrange-Funktion ableiten lassen.
Dann wird sich diese Eigenschaft der Lorentz-Kraft nämlich als eine Konsistenzbedingung ergeben, und
es werden dabei auch die inhomogenen Maxwell-Gleichungen eine Rolle spielen. Aber das geht natürlich
zu weit über die klassische Mechanik hinaus, als das wir es an dieser Stelle wirklich verstehen können.
Wir werden uns im folgenden auf rein mechanische Systeme beschränken, und im nächsten Kapitel den
Umgang mit Lagrange-Funktion ausführlich üben.
Aufgabe 11.26 Aus der elementaren Elektrodynamik ist bekannt, dass sich die Felder E und B nicht
ändern, wenn wir die Potenziale φ und A wie folgt eichtransformieren,
φ0 = φ −
1
∂t Λ,
c
A0 = A + ∇Λ,
61
(11.80)
wobei Λ irgendeine Funktion von Ort und Zeit ist. Das ergibt sich auch durch Einsetzen unmittelbar aus
(11.78). Die Lagrangefunktion L ändert sich jedoch, wenn wir diese Transformation durchführen. Man
zeige, dass die transformierte Funktion durch
L0 = L +
q dΛ
c dt
(11.81)
gegeben ist. Die Zeitableitung d/dt ist wie üblich so zu verstehen ist, dass wir die Funktion Λ erst entlang
einer Bahn auswerten, und das Ergebnis dann als Funktion von Ort und Geschwindigkeit darstellen.
Aufgabe 11.27 Man beweise folgenden allgemeinen Satz. Es sei L irgendeine Lagrange-Funktion auf einem Konfigurationsraum Q, die nicht einmal quadratisch in den Geschwindigkeiten sein muss. Sie wird in
einem beliebigen Koordinatensystem dargestellt als Funktion der Ortskoordinaten q α , der Geschwindigkeiten q̇ α und der Zeit t. Eine zweite Lagrange-Funktion L0 sei definiert durch
L0 = L +
dΛ
∂Λ
∂Λ
= L + α q̇ α +
,
dt
∂q
∂t
(11.82)
wobei Λ irgendeine Funktion der Orte q α und der Zeit t ist. Dann ergeben sich aus L und L0 dieselben
Bewegungsgleichungen (11.51). Verschiedene Lagrange-Funktionen L und L 0 führen also auf die gleichen
Bewegungsgleichungen, wenn sie sich nur um die totale Zeitableitung einer Funktion Λ unterscheiden.
62