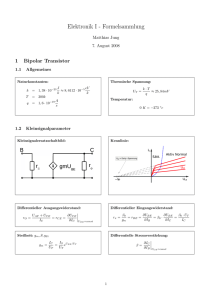
Kap IV Feldeffekt

BEL
Kap IV
32
Rainer
Feldeffekt - Transistoren
Steuerung mit elektrischem Feld
unipolare Leitung


leistungslos, keine Rückwirkung
n-Kanal- oder p-Kanal- FET’s
4.1 SPERRSCHICHT(J)-FET
Trennung der Steuerelektrode vom stromführenden Kanal durch pn-Sperrschicht
Steuerung über Kanalquerschnitt A: Steuerspannung bestimmt Sperrschichtdicke
Abb:
Beispiel: n-Kanal-JFET
24(1a) Zwei Kanalanschlüsse: Source (Quelle) S  Emitter
Drain (Senke) D  Kollektor
Steueranschluß:
Gate (Tor) G
 Basis
Spannung längs des n-Kanals von 0 (Source-Anschluß) bis +UDS (Drain-Anschluß) linear ansteigend
bei festem Potential auf der gesamten Gate-Elektrode keilförmig wachsende pn-Sperrschicht.
nur negative UGS-Werte gegenüber positivem Kanalbereich zulässig (Diode in Sperrichtung!)
24(1b) p-Kanal-J-FET
nur positive UGS-Werte gegenüber negativem Kanalbereich zulässig (Diode in Sperrichtung!)
24(2) Schaltzeichen, Zählpfeilsystem
* (Spannungs-)Steuerkennlinien
ID = f(UGS)
Parameter UDS
Abb:
(Übertragungskennlinien)Verlauf gemäß quadratischer Parabel:
24(3a) bei UGS = 0
fließt der größte Drain-Source-Strom ID, abhängig von UDS, solange UDS < |UP|
der Maximalwert IDSS (Drain-Source-Kurzschlußstrom) wird erreicht für UDS  |UP|
ab UGS = UP
erfolgt Kanalabschnürung (pinch off) mit ID = 0
* Ausgangskennlinienfeld
ID = f(UDS)
Parameter UGS
ohm’scher Bereich  ID prop. UDS  RDS = f(UGS)
Anwendung: steuerbarer Widerstand
Abschnürbereich 
ID nur von UGS abhängig
Anwendung: Kleinsignalverstärker
(entspr. Sättigungsbereich beim Transistor)
Ursache: keilförmig wachsende Sperrschicht zu D hin
für UDS = U(BR)DS:
Spannungsdurchbruch zwischen Gate-Elektrode und Kanal
siehe auch Eingangskennlinie
24(3c) Eingangskennlinie IG =f(UGS); IG im nA-Bereich << IB,vernachlässigbar, Spannungsdurchbruch
Abb:
für kleine UDS -Werte:
24(3b)
für größere UDS-Werte ( |UP|):
4.2 IG-FET insbes. MOSFET
Trennung der Steuerelektrode vom stromführenden Kanal durch Isolator ( Insulated Gate)
Steuerung über Kanalleitfähigkeit : Steuerspannung bestimmt Ladungsträgerkonzentration im Kanal
* MOSFET als wichtigster Vertreter ( Metall - Silizium-Oxyd - Semiconductor )
Abb:
25(1)
Grundlage ist die MOS-Kapazität (Aufbau in Planar-Technik):
Gate-Elektrode - Isolator - Halbleiter (Bulk B, beim n-Kanal-MOSFET das p-Substrat)
Spannung UGB (hier = UGS) verursacht Oberflächenladung auf G und entgegengesetzt gleich große auf
Halbleiteroberfläche  Leitfähigkeitsänderung des oberflächennahen Halbleiterbereichs (Kanal)
Beispiel: n-Kanal-MOSFET-Typen (Substrat aus p-Material), herstellbar in 2 Varianten:
25(1a) Verarmungstyp, D-Typ (Depletion) (selbstleitend):
leitfähiger n-Kanalbereich bereits eindiffundiert; zunehmende Abschnürung des Kanals für negativ
ansteigende UGS- Spannungen, ID = 0 für UGS -Spannungen negativer als UTO (Turn On)
25(1b) Anreicherungstyp, E-Typ (Enhancement) (selbstsperrend):
Kanal fehlt ohne Ansteuerung, erst ab UGS > UTH (Schwellspannung, auch UTO genannt) Bildung einer
n-leitenden „Inversions“-Schicht (n-Kanal), getrennt durch Verarmungszone vom übrigen p-Substrat
BEL
33
Rainer
Abb:
25(2)
MOSFET-Kennlinien analog JFET
Unterschied bei Verarmungstyp: auch pos. UGS zulässig, UTO entspricht UP
Anreicherungstyp: nur pos. UGS sinnvoll, Stromfluß erst ab UGS >UTO
restlicher Stromanstieg im Sättigungsbereich stärker
Gateströme Größenordnung pA, nochmals wesentlich kleiner als beim JFET
 noch kritischer in Bezug auf Zerstörung (Spannungsdurchbrüche) bei statischen Aufladungen
Abb:
Schaltzeichen aller MOSFET-Typen:
25(3) Verarmungstyp mit durchgehendem, Anreicherungstyp mit durchbrochenem DS-Anschlußbalken
Zusätzlicher Bulk-(B) Anschluß an Sustrat, häufig mit S verbunden
Gegenüberstellung MOSFET- BIPOLAR- Technologie bei Schaltkreisintegation
Vorteile:
MOSFET automatisch durch Sperrschicht vom Substrat getrennt, selbstisoliert
Steuerung leistungslos  höhere Integrationsdichte
Verarmungs- und Anreicherungs-Steuermoden sowie
Komplementärtransistoren (n- und p-Kanal: CMOS)  einfacherere Grundstrukturen
MOS-Kapazität eignet sich als Speicher-Grundbaustein
rel. große parasitäre Kapazität CMOS(UGB)  Reduzierung der Arbeitsgeschwindigkeit
nur rel. kleine Lastströme  bes.bei kapazitiver Last Begrenzung des Schaltverhaltens
optimaler Kompromiß: BICMOS-Technologie:
kombiniert CMOS-Strukturen mit schnellen bipolaren Treiberschaltungen auf einem Chip
Nachteile:
* IGBT (Insulated Gate Bipolar Transistor)
verbindet große Durchlaßströme (niederohmige Strombahnen) wie beim Bipolartransistor mit dem leistungslosen Steuerungsprinzip des MOSFET
Anwendung in der Leistungselektronik
4.3 Anwendungsbeispiele:
* JFET: Verstärker in Source-Schaltung
Unterschiede zur bipolaren Transistorstufe: Im Eingangskreis fließt „kein“ Strom, also nur Spannungen zur
potentialmäßigen Festlegung und Kleinsignal-Ansteuerung des Steueranschlusses Gate!
Die zur AP-Einstellung erforderliche negative Spannung UGS kann nicht von der pos. Betriebsspannung UB
abgeleitet werden; man legt statt dessen das Gate hochohmig (über R1) an Masse und hebt das S-Potential
mittels eines zusätzlichen Source-Widerstand RS um den Spannungsabfall URS = ID|AP * RS an.
Im Kleinsignal-Ersatzschaltbild fehlt rGS (rGS  , leistungslose Steuerung); zur Berechnung der gesteuerID
ten Stromquelle ist nur die Spannungssteuerkenngröße s =
| AP relevant
UGS
Geg: +UB = 15V
n-Kanal-JFET
Steuerkennlinie:
Schaltung:
20
ID[mA]
18
16
14
12
10
8
6
4
2
7 6
5
4
3
2
1 0
UGS [V]
C1 = 100nF, CS = 200µF, RG = 5k
BEL
34
Rainer
Geforderter Arbeitspunkt:
AP(9V/6mA)
Für diesen AP sollen folgende dyn. Kenndaten gelten:
rDS = 20k
und, zu entnehmen aus der SteuerKennlinie
s
Dimensionierung
für AP: R1, RS, RD
Kleinsignalersatzschaltbild:
Berechnung der Verstärkerdaten:
Gesamteingangswiderstand re
Spannungsverstärkung vu ohne GK
RS wechselsp.mäßig durch CS kurzgeschlossen
vu = -s*RD||rDS
Spannungsverstärkung vu mit GK (ohne CS)
Ersatz für Ausgangskreis:
vu  
s
* RD
1  s * RS
Ausgangswiderstand r2 (siehe GK) r2 = rDS*(1+s*RS)
Gesamtausgangswiderstand ra
Zahlenmäßig:
Der für die AP-Einstellung erforderliche rel. kleine Arbeitswiderstand RD bedeutet kleine Verstärkung.
 Verwendung eines nichtlinearen Lastwiderstandes (FET) mit hohem dynamischen Innenwiderstand (s.u.)
Frequenzgang:
untere Grenzfrequenz fu:
1
* Koppelkondensator C1: Frequenzabh. Spannungsteilung C1 - R1
 f u1 
2 * C1 * ( RG  R 1)
* Sourcekondensator CS (bei Gegenkopplung durch RD):
1
s * RD
|vu| steigt vom Wert
(für
<< RS, volle GK) bis zum Wert s* RD (RS kurzgeschlossen)
1  s * RS
CS
s
Dimensionierung siehe Emitterstufe mit GK
 fu 2 
2 * CS
BEL
35
Rainer
Zahlenmäßig:
obere Grenzfrequenz fo: physikalischesErsatzschaltbild des FET
maßgeblich sind die inneren FET-Kapazitäten
CGD, CGS Sperrschicht- bzw. MOS-Kapazitäten
zwischen Gate-Elektrode und Kanal
1
rGS vernachlässigbar: ab 500Hz >>
jCGS
CDS Drain-Source-Kapazität
obere Grenzfrequenzen für Eingangs- und Ausgangskreis, die niedrigere bestimmt fo
Prinzipieller Verlauf des Amplitudenfrequenzganges wie beim bipolaren Transistor
* CMOS Inverter / Verstärker
Antireihenschaltung (mit Richtungsvertauschung) zweier n- und p-Kanal Anreicherungs-MOSFET’s
Betriebspolaritäten für n- und p-Kanal-Typen:
n-Kanal-Anr.-Typ
UGS pos.:0 ...+UB
D
S
-UB
+UB
p-Kanal-Anr.-Typ
UGS neg.: 0 ...-UB
Masse
D
S
Masse
Wechselschalterprinzip der CMOS-Stufe bei gleichem Betrag der Schwellspannungen UTOn = -UTOp
und gleicher Transistorauslegung:
Schaltung:
u1 < UTOn
 Tn sperrend
Tp leitend (ohm’scher Bereich):
|UGSp| = |u1- UB| > |UTOp|
u2 = UB
u1 > UB-|UTOp|  Tp sperrend
Tn leitend (ohm’scher Bereich):
UGSn > UTOn
u2 = 0
u2
UB
UB/2
hieraus läßt sich die Übertragungskennlinie ableiten:

UB/2
u1
UB
BEL
36
Rainer
Hauptanwendung in der Digitaltechnik (CMOS-Logik), da in beiden Logikzuständen L und H kein Strom
fließt (Leistungsumsatz nur während des sehr kurzen Umschaltvorganges).
Anwendung als invertierender Verstärker:
UB
/ IB ) durch Festlegung von UGD = 0 für beide FET’s mit R1 = 10M
2
Schaltung:
Kleinsignalersatzschaltbild:
UGSn = |UGSp| bei gleichem IB
(FET’s wechselspannungsmäßig parallel)
 Arbeitspunkt AP (
Zahlenmäßig mit:
sn = sp = 3ma/V
rDSn = rDSp = 20k
R1 >> rDSn || rDSp
vu 
BEL
37
Kap.V
Rainer
Operationsverstärker
5.1 Schaltungsaufbau
* Eingangsstufe (T1, T2): Differenzverstärker
Abb:
28(1)
28(3)
2 Transistoren mit gemeinsamen Emitterwiderstand RE
Arbeitspunkteinstellung: Basisanschlüsse beider Transistoren gleichspannungsmäßig über niederohmige Signalquellen, gegebenenfalls Kurzschluß an Masse bzw. „virtuell“ an Masse (s.unten)
 Gemeinsamer Emitteranschluß auf festem Potential von ca. – 0,6V
 Strom teilt sich symmetrisch auf beide Systeme auf
vEmittersch.
Gegetaktansteuerung (zB.u1>0, u2 = 0)  IC1 = |IC2|:
Stromwaage
vD =
2
Gleichtaktaussteuerung (uD = 0, u1 = u2)  IC1 = IC2:
Gleichtaktunterdrückung vGl <<1
Im OP wird RE durch Konstantstromquelle ersetzt  RE  , vGl  0
(1a) * Zwischenverstärker (T3)
Verstärkung und Pegelverschiebung für UA = 0 bei UP = UN = 0
Gesamtverstärkung (Stufe 1 und Stufe 2) sehr groß, >10.000 entspr. 80 dB
Gleichspannungsverstärker zufolge Gleichspannungskoppelung aller Stufen
(1a) * Endstufe (T4)
hier Kollektorschaltung, häufig Gegentaktendstufe zur Leistungsverstärkung
* Schaltungssymbol
Abb:
28
(1b)
P(+):
N(-):
A:
pos. Eingang (nicht invertierend)  UP >0  UA (= v0* UP) > 0
neg. Eingang (invertierend)
 Un >0  UA (= v0* Un) < 0
Differenzansteuerung UD zwischen P und N
Ausgang gegen gemeinsamen Massepunkt (OP hat keinen herausgeführten Masseanschluß!)
meist symmetrische Spannungsversorgung, 2 betragsmäßig gleiche Quellen +UB und -UB
* Übertragungskennlinie UA = f(UD)
Abb: Realisierung der dargestellten Kennlinie zB. mit UP = UD, Un = 0
28 sehr steile Kennlinie zufolge hoher Verstärkung v0 = 86dB  sehr kleiner Aussteuerbereich
UA
UA
=
(für UOS  0)
UD
UD
= Verstärkung ohne Gegenkopplungsbeschaltung (normaler Betriebsfall)
linearer Kennlinienverlauf bis zur Sättigung: UAmax  +UB -1 bis 2V, UAmin  -UB +1 bis 2V
Offsetspannung UOS: Eingangsdifferenzspannung bei UA = 0
(2b) Offsetabgleich = Nullpunktskorrektur (intern oder extern durch Zusatzbeschaltung)
(2c) Nullpunktstörungen durch Temperatur, Betriebsspannung, Gleichtaktaussteuerung
zB. UOST = 10µV/K (am Eingang) bedeutet am Ausgang des leerlaufenden OP bereits 0,2V/K
(2a) „Leerlauf“-Verstärkung v0 =
5.2 Lineare Verstärkerschaltungen, idealer OP
normaler Betriebsfall: zusätzliche
exterene Rückkopplungsbeschaltung (Gegenkopplung)
Verstärkung nur festgelegt durch 2 Widerstände
Abb: Eigenschaften des idealen OP:
28 Leerlaufverstärkung (ohne Beschaltung) v0 ,
(1b) Differenzeingangswiderstand rD  
 iN = iP = 0 und uD = 0 (solange uA im aktiven Arbeitsbereich ist, muß uE = uD  0 gehen)
N- und P-Eingang befinden sich „virtuell“ auf gleichem Potential – ohne galvanische Verbindung !
Ausgangswiderstand ra  0
keine Offset-Spannungen und –Ströme
keine Frequenzabhängigkeiten
BEL
38
Rainer
* invertierender Verstärker:
Ansteuerung von N (invertierender Eingang), P an Masse
 RN Steuerwiderstand (an N)
 Rf Rückkopplungswiderst.(feed-back) zwischen A und N
Verstärkung: uN = uD+uP = 0 (uq am Eingang):
N-Eingang liegt „virtuell“ an Masse
uq
 ie 
RN
ua stellt sich wegen iN = 0 so ein, daß ie
über Rf abfließen kann
0  ua
 ie  if 
Rf
ua ie * Rf  Rf
v


uq ie * RN
RN
Rf
 v
RN
Schaltung:
Eingangswiderstand: re 
uq
ie

re = RN
Inverter: v = -1
Schaltung:
realisierbar mit Rf = RN
Anwendung: Phasendrehung um 180°
Summierschaltung, Subtrahierschaltung
Berechnung nach dem Überlagerungssatz:
Summierschaltung:
Subtrahierschaltung:
Geg.uq1, uq2 = 0  Wirkung ua1
Geg.uq2, uq1 = 0  Wirkung ua2
 resultierende Gesamtwirkung = ua = ua1+ ua2
Berechnung:
Berechnung:
BEL
39
Rainer
* nicht invertierender Verstärker:
Schaltung:
Ansteuerung von P (invertierender Eingang)
Rückkopplungsnetzwerk an N (Gegenkoppl.erforderlich!)
Potential von P liegt „virtuell“ auf Potential von N
Verstärkung:
uN = ua *
RN
RN  Rf
uq = up = uN = ua *
v

RN
RN  Rf
ua RN  Rf

uq
RN
v 1
Rf
RN
Eingangswiderstand: uP an P, iP =0

re  
„Eins“-Verstärker: v = +1
Schaltung:
Realisierung z.B. mit Rf = 0 und RN  
Anwendung: Impedanzwandlung
Summierschaltung, Subtrahierschaltung:
Summierschaltung:
Berechnung:
Subtrahierschaltung:
Berechnung:
BEL
40
Rainer
* Integrierer:
Schaltung:


uN  0: „virtueller“ Nullpunkt
uq
ie 
R
uq
ie+iC = 0  iC  
R
duC
dua
iC  C *
 C*
dt
dt
ua( t )  

1
* uq( t )dt
TI
mit Integrator-Zeitkonstante
TI = R*C
Eingangsgleichspannung:
zB. uq = -1V (Laborversuch)
1V
 ua =
* t  Rampenspannung bis zur OP-Sättigung
TI
Sinusförmige Eingangsspannung:
Rechnung mit komplexen Widerständen:
1
Zf
1
jC
v= 


ZN
R
j * TI
1
 I fI
1
|v| =
mit I =


 * TI  f
TI
Amplitudenfrequenzgang (Bode-Diagramm):
mit 20 dB/Dekade fallende Gerade, v = 0dB bei f = fI (=10kHz)
|v|/dB
60
40
20
f/kHz
0
0.1
1
10
100
-20
5.3 Realer OP
Leerlaufverstärkung (unbeschalteter OP): v0 endlich, bei höheren Signalfrequenzen stark abfallend
Differenz-Eingangsspannung
 UD = UN -UP  0
Ausgangswiderstand
 ra  0
Zusätzliche Störgrößen:
Offsetspannung UOS
IN  IP
Eingangsruheströme IN, IP  0: angegeben als
mittlerer Eingangsruhestrom
IIB =
2
und
Offsetstrom
IOS = | IN - IP |
Die endliche Leerlaufverstärkung v0 hat einen relativ geringen Einfluß auf die Verstärkerdaten des beschalteten OP bei Gleichspannungsbetrieb und bei niedrigen Signalfrequenzen; bei höheren Frequenzen
führt die Frequenzabhängigkeit von v0 zu einem erheblichen Einfluß auf Verstärkung und Stabilität.
* Eingangswiderstand re’
Im ESB charakterisiert durch Differenzeingangswiderstand rD zwischen N und P  einige M
und Gleichtakteingangswiderstände rGl gegen Masse
 einige 100 M
Berechnung an Hand der Ersatzschaltung für den idealen OP + geeigneter Erweiterung des ESB für die
beiden Eingänge (Beispiel siehe unten, Ausgangswiderstand, Verstärkung). Ergebnis:
invertierender Verstärker:
re’= RN 
Rf
v
 RN * (1  )  RN
1  v0
v0
nicht invertierender Verstärker: re’= rD * (1 
v0
) || rGl
v
mit v = 
Rf
RN
mit v = 1 +
Rf
RN
(ideal: re = RN)
(ideal: re  )
BEL
41
Rainer
Beispiel:
v0 = 80dB, v = 100
rD = 1M
rGl = 100M
re’ = 50M !
* Ausgangswiderstand ra’
Im Ersatzschaltbild für den Ausgangskreis des beschalteten OP erscheint der endliche Ausgangswiderstand r a
des realen OP (dyn. Kenngröße) als „Innenwiderstand“ ra der Ersatzquelle v0*uD:
Erweitertes Ersatzschaltbid:
resultierenderAusgangswiderstand ra’
bei Beschaltung als Verstärker:
ua = ia* ra + v0 * uD (Rf hochohmig gegen ra) mit
RN
uD = - uN = - ua*
RN  Rf
RN
 ua (1 + v0*
) = i a* r a
RN  Rf
ua
r a’ =
ia
ra’ =
ra
RN
1  v0 *
RN  Rf
 ra *
v
v0
Beispiel: v0 = 100 dB für tiefe Frequenzen,
60 dB bei 1kHz (Meßfrequenz)
v = 40 dB, ra = 75
* Spannungsverstärkung v’:
nicht invertierender Verstärker:
Rf
RN
mit v = 1+
uq = uN + uD
v’ =
uN = ua*
und
uD =
RN
RN  Rf
ua
v0
RN
1
+
)
RN  Rf v 0
uq = ua (
 v’ =
mit
ua
=
uq
v0
RN
1  v0 *
RN  Rf
v
v
1
v0
 v * (1 
oder mit v =
v
)v
v0
Beispiel: v0 = 80 dB (bei 100Hz)
v = 100
invertierender Verstärker:
mit
Rf
v=RN
Rf
RN  Rf  v * (1  v )  v
 v’ = 
RN
v0
1  v0 *
RN  Rf
v0 *
RN  Rf
RN
BEL
42
Rainer
Maßgeblich für den Fehler zwischen Berechnung mit idealem OP und realem OP ist also das Verhältnis
v/v0, also das Verhältnis von der (bei idealem OP) nur durch Rf und RN festgelegten Verstärkung zur Leerlaufverstärkung.
* Frequenzgang und Stabilität
Leerlaufverstärkung: Verstärkungsabfall + Phasendrehung bei höheren Frequenzen
Stabilitätsprobleme bei beschaltetem OP(Gegenkopplung) zufolge zusätzlicher Phasendrehung
OP besteht aus mehreren in Serie geschaltetenVerstärkerstufen, jeweils mit Tiefpaßcharakter
OP-Modell, „schwach korrigiert“:
v1
Ue =UD
OP
v2
1 =
R1C1
2 =
R2C2
U1
Ua
verteilt auf die beiden Stufen:
Ue
1
1
Grenzfrequenzen der beiden Tiefpässe: fg1 =
, fg2 =
2 * 1
2 * 2
Komplexe Gesamtverstärkung
Beispiel:
v0 =
v0|f0 = 105
entsprechend 100dB
fg1 = 100Hz, fg2 = 100kHz
v0=
Ua
U1 Ua
*
Ue U1
|v0| [dB]
100
 Amplituden-(Frequenz)gang |v0(f)|:
|v0| = const.100dB bei „tiefen“ Frequenzen
f1
ab 1. Grenzfrequenz fg1: |v0|  v0|f0*
f
 Verstärkungsabfall um 20dB/Dekade
ab 2. Grenzfrequenz fg2: 1 und 2 wirksam,
log.Darstellung ergibt
U1
Ua
Addition von
und
Ue
U1
 Verstärkungsabfall um 40dB/Dekade
 Phasen-(Frequenz)gang 0(f):
0 = - 45° bei fg1, 0  -90° ab f>> fg1( TP, 1)
0  -135° bei fg2 (zusätzlich -45° zufolge 2)
0  -180° ab f>> fg2
80
60
40
20
f[Hz]
0
1
10
0
-90
-180
-270
-360
0(f)[°]
100
1k
10k
100k
1M
BEL
43
Rainer
Problem beim beschalteten OP:
Aus Gegenkopplung bei Beschaltung des Op (GK = -180°) wird u.U. bei hohen Frequenzen Mitkopplung
 Stabilitätsprobleme, Schwingneigung maßgebliche Größe für die Stabilität ist die
komplexe Schleifenverstärkung vS: OP und Rückkopplung bei N aufgetrennt, ohne Signalquelle
Rf
RN
N
U a’
vS =
UN

+
k
-v0
UN
Ua
U a’
Ua
Ua ' Ua Ua '
RN
=
*
= -v0*k = -v0*
UN UN Ua
RN  Rf
Amplitudengang:
Phasengang:
1
 gesamter Verlauf um 20 dB abgesenkt)
10
S (f) = 0(f) -180° (zufolge neg. Vorzeichen von v0)
|vS|(f) = |v0|(f)*k (z.B. k =
 Ist die Schleife geschlossen, kommt es mit Sicherheit bei der Frequenz zum Schwingen, bei der
vS = 1
wird, das heißt |vS| = 1
und S = 0° oder 360°
 Stabilitätskriterium:
vS < 1 bevor S = 360° erreicht
Charakterisierung der Stabilität durch den Begriff „Phasenreserve“ ( hier etwa 45°)
OP-Modell, „stark korrigiert“ :
|v0| [dB]
Stabilität (ausreichende Phasenreserve) durch
zusätzliche Korrektur des Frequenzganges v0
(„Frequenzkompensation“): interne bzw. externe Kompensation (Anschluß für externes C)
 Herabsetzen der 1. Grenzfrequenz fg1 auf f0
Beispiel: fg1 = f0 10Hz : so niedrig, daß der
Frequenzgang v0 nahezu bis zur Transitfrequenz fT (|v0| = 0dB) nur durch den 1.TP (nur
1 wirksam) beschrieben werden kann:
 Frequenzgang der Leerlaufverstärkung (bei
starker Korrektur) v0(f):
 v0 =
v0 | f
 0
f
1  j*
f0
|v0| =
v0 | f
100
80
60
40
20
 0


f 


f0
2
1  j * 
f[Hz]
0
1
10
0 maximal  -90°
|v0| = const.100dB bei „tiefen“ Frequenzen
f0
ab Grenzfrequenz f0  10Hz: |v0|  v0| f  0*
f
Verstärkungsabfall von 20dB/Dekade
|v0| =1 0dB bei Transitfrequenz fT (1MHz)
0
-90
-180
Frequenzgang der Schleifenverstärkung vS:
Analog  Phasenreserve  45° bei der
kritischen Frequenz, bei der |vS| =1 0dB wird
(= Transitfrequenz fT, auch „Schnittfrequenz“ fS)
-270
-360
0(f)[°]
100
1k
10k
100k
1M
BEL
44
Rainer
Frequenzgang des beschalteten OP (nicht invertierend) vu:
Berechnung siehe Abschnitt Spannungsverstärkung des realen OP, wobei wegen des Frequenzgangs von v0
RN
komplexen Spannungen benutzt werden. Mit
= k wird:
RN  Rf
Ua
v0
v0


 vu 
|v0|/dB
Uq 1  v0 * k 1  vS
Diskussion des Amplituden-(Frequenz)ganges:
für unteren Frequenzbereich, solange vS >>1 ist, gilt:
v0
1
vu 
= = v (im Beispiel 20dB)
 vS k
für hohe Frequenzen mit vS <<1 gilt:
f0
vu  v0; |vu| = v0| f  0*
(-20dB/Dekade)
f
1
„Schnittfrequenz“ fS : bei |v0|(f) = (= const.)
k
also Frequenz, bei der sich diese beiden Frequenzgänge, asymptotisch verlängert, schneiden
= „Eck“-frequenz (100kHz) und damit
v
= Grenzfrequenz fg des beschalteten OP mit |vu| =
2
100
80
60
40
20
f/Hz
0
1
10
100
1k
10k
100k
1M
Transitfrequenz fT (definiert durch |vu| = 1): fT = 1MHz
Ergebnis: bei einer Grenzfrequenz f0 des leerlaufenden OP von 10Hz erreicht der beschalteten OP 100kHz !
bei inv.Verstärker-Beschaltung: analog (|v| meist  1/k)
Verstärkungs-Bandbreite-Produkt vi*fi = const:
charakteristische Kenngröße den jeweiligen OP, hier 106
v0*f0 = v*fg = 1*fT
5.4 Datenblätter OP µA 741
Abb: Eigenschaften / Anwendung
33 Schaltbild /
Grundstruktur
Anschlußanordnung interne Frequenzkompensation
externe Offsetspannungskorrektur
Abb: Grenzdaten
34 Kenndaten
siehe Stichworte + Überschwingen und
Anstiegszeit (Slew Rate: SLR)
maximale Anstigsgeschwindigkeit begrenzt Ausgangsspannungshub US+ -US-  2*|US|,
bereits bei Frequenzen, die wesentlich niedriger sind als fg (festgelegt durch Beschaltung):
bei sinusförmiger Aussteuerung u = û*sin(t) ist SLR zu berechnen aus der maximal zulässidu
ge Anstiegsgeschwindigkeit
| max = û*
dt
V
Beispiel: SLR = 0,5
s
US+ = |US-| = û = 13V
Abb:
36 für höhere Frequenzen: ûAmax proportional 1/f
Abb: Diagramme:
Abhängigkeiten der Kenndaten von
35,36
*Spannungsversorgung
*Temperatur
*Frequenz
*Lastwiderstand
zB. Leerlaufverstärkung: vu0 (  US), vu0(f)  Bodediagramm und Phasengang, fg
Ausgangsspannung:
UQss (  US), U Qss(f) ( SLR), UQss(RL)
Ein- /Ausgangswiderstand: RI /RQ in Abh. von T, f
BEL
45
Rainer
5.5 Nichtlineare OP-Schaltungen
OP ohne Gegenkopplung ( Verstärkung v0 ), ohne Frequenzkompensation, hohe SLR-Werte
OP befindet sich statisch in einem der übersteuerten Zustände Ua max bzw. Ua min
 Sprunghaftes Umschalten zwischen diesen beiden Zuständen bei bestimmten Bedingungen am Eingang
Beschleunigung des Umschaltens meist durch zusätzliche Mitkopplung
* Komparatoren
Schaltung:
Zeitdiagramme von Eingangs- und Ausgangsspannung:
ue
UV
0
t
ua
Ua max
„vergleicht“ue mit Vergleichsspannung UV
t
0
Überschreitet die Eingangsspannung
Ua min
ue = uN die Vergleichsspannung UV an P
nur um einige mV kommt es zum sprunghaften Umschalten von Ua max nach Ua min
 ua = Rechteckspannung, Umschaltpunkte bei ue  UV; Umschaltgeschwindgkeit festgelegt durch SLR
* Trigger / Impulsformer
Zur „Umformung“ beliebiger periodischer Signale in Rechtecksignale
Beispiel: Invertierender Schmitt -Trigger:
Grundschaltung:
OP mit Mitkopplung zur Beschleunigung des
Umschaltvorganges
Als Umschaltpunkte (Triggerpunkte UE1 bzw UE2) sind diejenigen Eingangsspannungswerte definiert, bei
denen die Umschaltung erfolgt:
Umschaltung von Ua max nach Ua min
bei uN ( = ue) = UE1
Umschaltung von Ua min nach Ua max
bei uN = UE2
R2
Sie lassen sich durch die Mitkopplungsbeschaltung festlegen:  uN = uP = Ua max/min*
R1  R 2
Hysteresespannung UH = UE1 + |UE2|
Die Funktionsweise der Schaltung läßt sich durch einfache Potentialbetrachtungen erläutern, wobei man von
einem der beiden statischen Betriebszustände (und dem dazu „passenden“ Eingangsspannungsbereich)
ausgeht:
Wahl des Ausgangszustandes bei t = 0: Ua max (z.B. = 10V)
Wahl der Eingangswechselspannung: Dreieck mit ûe (z..B. = 6V)
Wahl des Teilerverhälnisses so, daß sich für den Triggerpunkt UE1 (z.B. = 5V) ergibt
 stabiler Betriebszustand Ua max, solange ue = uN < UE1 ist
BEL
46
Rainer
Zeitdiagramme von Eingangs- und Ausgangsspannung:
ue
UE1
t
0
UE2
erreicht ue = UE1 (Triggerpegel):
Umschalten von Ua max nach Ua min und
R2
uP = Ua min *
= UE2 (= -5V)
R1  R 2
 stabiler Betriebszustand Ua min ( = -10V),
solange ue = uN > UE2 (= -5V ) ist
Rückkippen, sobald ue = UE2 (= -5V) wird
ua
Übertragungskennlinie: ua = f(ue)
ua
Ua max
t
0
ue
Ua-min
Verschiebung der Hysterese durch Einfügen einer zusätzlichen Vergleichsspannung UV
* Multivibrator
Schmitt-Trigger (OP, mitgekoppelt über R1, R2) + zusätzliche Rückkopplung über Rf auf invertierenden
Eingang und CN gegen Masse  Eigentriggerung gemäß Zeitkonstante  = Rf * CN
 selbst schwingende Stufe
Schaltung:
Zeitdiagramme von uN und ua:
10
u[V]
t[ms]
0
10
20
-10
R2
R1  R 2
und die Aufladespannung uC am Komdensator CN (= uP) habe gerade diesen Triggerpegel UT+ = uN erreicht.
 Umschaltung von Ua max  Ua min; uN nimmt den betragsmäßig gleichen aber negativen Wert UT- an. von
t = 0 bis zum nächsten Umschalten von Ua min  Ua max liegt somit CN über Rf an Ua min
 uC(t) verläuft nach e-Potenz vom Startpotential uN (= uP = UT+) gegen den Endwert Ua min:
Ausgangszustand bei t  0: Ua max , uN = Ua max *
t
uC(t) = [(Ua max+UT+)* e  ] - Ua max . Die Umladung wird gestoppt, sobald uC(t) den nächsten Triggerpunkt UT- erreicht und damit das Rück-Kippen von Ua max  Ua min auslöst. Für diesen Zeitpunkt t1 gilt mit
T
T
t1= : uC(t1) = UT- = [(Ua max+UT+)* e 2  ] - Ua max , und die Auswertung liefert mit  = Rf *CN :
2
1
1
1 R1
R2
 Periodendauer T = 2 * ln(1+2*
) und Frequenz f  

*
R
2
T 2 * ln(1  2 * ) 4 R 2
R1
R1
Beispiel:
Kap VI
US = 10V
CN = 1µF
Rf = 10k
R1 = 4k
R2 = 1k
Schaltkreis-Integration
BEL
47
Rainer
Ausgangsprodukt :Wafer
p- oder n- dotierte Halbleiterscheibe, einige Zehntel-mm dick, bis zu 200 mm Durchmesser
hergestellt aus hochreinem Si (Reinheit 10-10 ) + Zusatz von Dotierungsmaterialien (10-9), polykristallin
Einkristall, mit Saatkristall aus Schmelze gezogen, bis zu 50 kg schwer, mehrere Meter lang
Zonenschmelzverfahren: Wandern einer schmalen Schmelzzone durch Einkristall, zur Reinigung
Abb: Flußdiagramm zur Herstellung von Halbleitern und integrierten Schaltkreisen (Integrated Circuit's)
48(1) Wafer + Schichterzeugung und Schichtstrukturierung in 6 bis 12 Durchläufen
pro Wafer je nach Größe des IC oder des Einzelhalbleiters sehr viele identische Strukturen
Inspektion zur Aussortierung defekter Einzelstrukturen
Herausschneiden der brauchbaren Kreise, Montage im Gehäuse und Abschlußtest
Abb:
48(2)
Abb:
48(4)
Abb:
48(3)
Abb:
48(4)
Schichterzeugung: Ablagerung dünner Schichten von Lack, Metall und anderem Material auf Wafer
* Aufschleudern zB. von Fotolack
* Aufdampfen: Metallfilm-Ablagerung (für Leiterbahnen) mittels Aufdampfanlage als Beispiel
Verdampfen der Metallschmelze mittels Elektronenstrahl, gleichmäßige Atomablagerung auf Wafern
* Epitaxie: Aufwachsen einer einkristallinen Schicht des gleichen oder entgegengesetzten Halbleitertyps
aus gasförmiger Phase auf die Halbleiter-Substrat-Oberfl. (Erhaltung der Kristallorientierung!)
zB. Ablagerung von SiCl4 + AsH3 (in Gasphase Si- + As-Donator-Atome) auf Si-Substrat bei1000°C
* Chemische Dampfabscheidung (Chemical Vapor Deposition, CVD)
Ablagerung dünner Schichten von Si, SiO2 (Isolierschicht) , Metallen (zB.Wolfram) aus Dampfphase
als Beispiel Oxidationsvorgang bei SiO2 -Maske
* Kathodenzerstäubung (Sputterprozess)
beschleunigte Gas-Ionen schlagen aus Katode (Quellwerkstoff) Metallatome heraus,die sich auf Wafer
(Anode) niederschlagen
Schichtstrukturierung zur geometrischen Anordnung von Halbleiterbereichen, Leiterbahnen usw.
* Fotolithographie und Ätzvorgang am Beispiel des Aufbringens einer Leiterbahn
Metallfilm auf ganzem Substrat, darauf Fotolackschicht
Belichtung des Wafers mit UV-Licht durch gewünschte Maske (Lay-out)
Entwickeln und Auswaschen der nicht benötigten Lackbereiche
Abätzen der nicht bedeckten Metallschichtbereiche, Entfernen des Fotolackstreifens über Leiterbahn
* Dotierung zum strukturmäßig festgelegten Einbau von Dotieratomen in n- oder p-Material
Ätzvorgang durch SiO2-Schicht (lithographisch) mit F-Atomen, die mit dem Si reagieren (trocken)
Dotierung mittels Diffusion: Einwandern der Dotieratome aus Gasphase bei Aufheizung zufolge Konzentrationsgefälle,Überkompensation des p-Materials  n-Zone
Ionenimplantation: Beschuß mit Dotierstoff-Ionen (bis 500kV beschleunigt)
aufwendiger, genauere Einstellung von Dotier-Mengen und -Profilen
Vorteile der Schaltingsintegration
* billige Massenproduktion, sehr viele identische Einzelschaltungen pro Wafer
* höhere Zuverlässigkeit (zB. wesentlich weniger Lötstellen....)
* Verkleinerung der Abmessungen, höhere Integrationsdichte (derzeit 0.5µ-Strukturen)
Begrenzung der Schaltungskomplexität durch Rückgang der Chip-Ausbeute
Abb:
49(1)
49(2)
49(3)
49(4)
Beispiel: Integration eines Spitzenwertgeichrichters
* Isolation: an der Chipoberfläche durch SiO2-Schicht
im Innern zur Trennung der Dioden durch zusätzliche p-n-Übergänge in Sperrrichtung
* Widerstände: dotiertes Substrat oder Widerstandsmaterial geeigneter Abmessung (50 bis 10k)
* Kondensator: Metallfilm-SiO2-n+Substrat - Kombination; Vaiante "Graben"-Technik (VMOS)
* Fertigungsschritte für Schnitt durch den Chip in Höhe von D1 und C:
n-Diffusion
Diode D1, n-Bereich
p-Diffusion
Diode D1, p-Bereich; Bodenelektrode C, p+Bereich
Isolation Dielektrikum C
Ätzen
der Diodenkonfiguration
Metallfilm + Konfiguration von Deckelektrode C, Verbindung von C und n-Anschluß D1, Kontaktfläche für p-Anschluß D1
Schutzüberzug + Freiätzen der Anschlußflächen