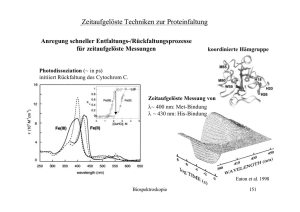
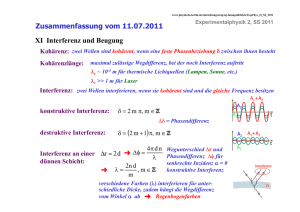
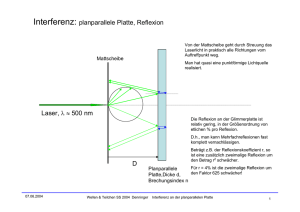
Klausur Aufgaben Informatik
Werbung

OW_03_02 Optik und Wellen Interferenz an dünnen Schichten Unterrichtliche Voraussetzungen: Reflexion von Wellen Interferenz Entspiegelung Literaturangaben: Verfasser: Peter Bastgen Gymn. Erftstadt Lechenich Dr. Jos. Fieger Straße 50374 Erftstadt 1 GK/LK LK Physik Jgst: Klausur-Nr. Datum: Aufgabe 0 a) Diskutieren Sie die Interferenz an dünnen Schichten allgemein, indem Sie die den Zusammenhang zwischen Helligkeitsmaximum, Schichtdicke, Einfallswinkel und Brechungsindex herleiten. 1 2 E A C d n B 1´ 2´ b) GehenSie davon aus, daß die Transmission des Lichtes bei einer gegebenen dünnen Schicht 96% beträgt. Was kann man dann über die Intensität des primär reflektierten (1) und des damit interferierenden zweiten Strahls (2) sagen? c) Diskutieren Sie die Entspiegelung von Brillengläsern. d) Wie erkärt sich der schwarze Fleck bei Reflexion von weißem Licht auf einer dünnen Seifenblase? e) Unter einem Winkel von 15° beobachtet man einen rot erscheinenden Lichtstrahl der Wellenlänge von 650 nm. Wie dick ist die betrachtete Schicht (n=1,4)? 2 Lösung zu a) 0 1 2 E A C d n B 1´ 2´ Die geometrische Wegdifferenz beträgt AB + BC - AE. Die optische Wegdifferenz beträgt (wegen unterschiedlicher Lichtgeschwindigkeit) n ( AB + BC ) - AE. Es gilt : ABBC 2d und AE = 2 d tan sin (Nachweis!) cos Mit dem Brechungsgesetz sin n erhält man dann sin n ( AB + BC ) - AE = 2d n 2 sin 2 Berücksichtigt man nun noch den Phasensprung von bei der Reflexion am dichteren Medium bei A so ergibt sich insgesamt eine Gangdifferenz von 2d n 2 sin 2 2 Bei einer Gangdifferenz von ganzzahligen Vielfachen der Wellenlänge ergibt sich also unter dem Betrachtungswinkel ein Helligkeitsmaximum für eine bestimmte Wellenlänge. Analog ergibts ich bei einer Gangdifferenz von /2 eine Auslöschung. Die beobachtete Farbe hängt also insbesondere von der Schichtdicke, dem Beobachtungswinkel und dem Brechungsindex des Mediums ab. 3 Lösung zu b) Bei Übergang von Luft nach Glas geht etwa 96% der Intensität durch die Grenzschicht, d.h. etwa 4% werden reflektiert. Strahl 1 ist einmal reflektiert worden und hat somit 4% der anfänglichen Intensität. Strahl 2 hat die Grenzschicht zweimal durchsetzt und ist einmal reflektiert worden; er besitzt daher noch den Anteil 0,96 x 0,04 x 0,96 = 0,037 4%. Damit sind die Intensitäten der beiden betrachteten interferierenden Wellen in etwa gleich: Wellenberg und Wellental löschen sich ggf. vollständig aus, was zu einem besonders kontrastreichen Interferenzmuster führt. Lösung zu c) Denkt man sich eine dünne Platte auf einen Glasklotz (Brille) aufgeklebt, und die Materialien so gewählt, daß n Luft-Schicht und n Schicht-Glas in einem Spektralbereich annähernd gleich sind, so wird von jeder der beiden Grenzschichten ein etwa gleicher Bruchteil Strahlungsleistung reflektiert. Wählt man die Schichtdicke so, daß für eine mittlere Wellenlänge m des Bereiches der Gangunterschied zwischen den Strahlen = m/2 ist, dann heben sie sich durch Interferenz auf und die gesamte Strahlungsleistung dringt in den Glasklotz ohne Reflexionsverlust ein. Für benachbarte Wellenlängen ist die Entspiegelung nur noch unvollkommen, aber für viele praktische Zwecke noch völlig ausreichend. Lösung zu d) Ist die Seifenblase nach einiger Zeit im oberen Bereich so dünn, daß der optische Weg innerhalb der Seifenblasenhaut praktisch vernachlässigbar wird, spielt zwischen den benachbarten Strahlen 1 und 2 nur noch der Phasensprung eine Rolle und unabhängig vonm Einfallswinkel und der Wellenlänge des Lichtes kommt es zur destruktiven Interferenz: Die Transmission liegt nahezu bei 100%, weshalb ein Loch in der Blase zu sein scheint. Ist der Hintergrund schwarz, erscheint das Loch ebenfalls schwarz. 4 Lösung zu e) Gemäß 2 ergibt sich für die Schichtdicke 1 = 2d n 2 sin 2 2 d 2 4 n sin 2 2d n 2 sin 2 650 nm 4 14 , sin 15 2 2 118 10 9 m Diese Rechnung gilt, falls die beobachete rote Farbe durch Interferenz zweier Strahlen mit einem Gangunterschied der einfachen Wellenlänge zu beobachten war. 5