Laser, λ ≈ 500 nm D Interferenz: planparallele Platte, Reflexion

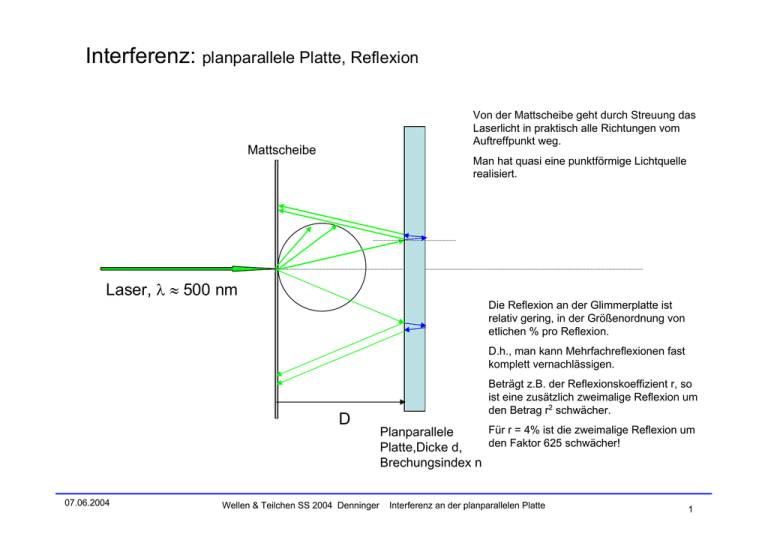
Interferenz: planparallele Platte, Reflexion
Von der Mattscheibe geht durch Streuung das
Laserlicht in praktisch alle Richtungen vom
Auftreffpunkt weg.
Mattscheibe
Man hat quasi eine punktförmige Lichtquelle
realisiert.
Laser, λ ≈ 500 nm
Die Reflexion an der Glimmerplatte ist
relativ gering, in der Größenordnung von
etlichen % pro Reflexion.
D.h., man kann Mehrfachreflexionen fast
komplett vernachlässigen.
D
07.06.2004
Wellen & Teilchen SS 2004 Denninger
Beträgt z.B. der Reflexionskoeffizient r, so
ist eine zusätzlich zweimalige Reflexion um
den Betrag r2 schwächer.
Für r = 4% ist die zweimalige Reflexion um
Planparallele
den Faktor 625 schwächer!
Platte,Dicke d,
Brechungsindex n
Interferenz an der planparallelen Platte
1
Planparallele Platte, n = 1.5
Interferogramme in Reflexion 30mmx30mm
30mm
-15
-10
-5
0
5
10
15 -15
-10
D = 20 mm
D = 20 mm
D = 100 µm
D = 50 µm
λ = 500 nm
λ = 500 nm
07.06.2004
Wellen & Teilchen SS 2004 Denninger
-5
0
Interferenz an der planparallelen Platte
5
10
15
2
Herleitung der Interferenzbedingungen
(1)
d
cos(α ′)
(2)
Die Teilwelle (1) legt im Material den Weg 2 ⋅
zurück.
∆1
Da dies im Material mit dem Brechungsindex n
geschieht, ist die optische Wegdifferenz:
∆1 = 2⋅ n ⋅ d
cos(α ′)
α′
α
∆2
Der Teilstrahl 2 hat in der Luft einen
Gangunterschied ∆ 2 , welcher sich durch
Geometrie zu ∆ 2 = 2 ⋅ d ⋅ tan(α ′) ⋅ sin(α )
bestimmt.
Die Beziehung zwischen α und α’ gewinnt
man aus dem Snelliuschen Brechungsgesetz:
2⋅ n ⋅ d
n2
∆1 = 2⋅ n ⋅ d = 2⋅ n ⋅ d2 =
=
2
d
cos α ′
1 − sin α ′
1 − sin 2α /n 2
n 2 − sin 2α
∆ 2 = 2d ⋅ tan α ′ ⋅ sin α = 2d ⋅
Gangunterschied:
07.06.2004
Brechungsindex n
n ⋅ sin α ′ = sin α
Bei der Reflexion des Teilstrahles (2) am optisch
dichteren Medium (der Platte) tritt zusätzlich eine
Phasensprung von π, also eine Verschiebung um
λ/2 auf. Das optisch dichtere Medium hat elektrisch
einen Wellenwiderstand kleiner als das Vakuum.
sin α
sin α ′
⋅ sin α = 2d
cos α ′
n 2 − sin2α
2
∆ = ∆ 1 − ∆ 2 + λ = 2d n 2 − sin2α + λ
2
2
Wellen & Teilchen SS 2004 Denninger
Dicke d
Diese beiden Teilstrahlen (1) und (2)
interferieren unter dem Winkel α
Interferenz an der planparallelen Platte
3
Diese Interferenz kann konstruktiv oder destruktiv sein:
∆ = 2d n 2 − sin2α + λ = m ⋅ λ ,
2
∆ = 2d n 2 − sin2α + λ =
2
Maximum
2m + 1
⋅ λ,
2
0
Ganzzahliges Vielfaches der Wellenlänge
m = 0,1, 2,3,..
Maximum
Minimum
λ
2
Für destruktive Interferenz:
Ungeradzahliges Vielfaches der halben Wellenlänge
Maximum
Gangunterschied ∆
Minimum
2λ
2
Für konstruktive Interferenz:
m = 0,1, 2,3,..
3λ
2
4λ
2
Da der Gangunterschied vom Winkel α abhängt, ergeben
sich in der Beobachtung konzentrische Kreise mit
abwechselnden Minima und Maxima.
07.06.2004
Wellen & Teilchen SS 2004 Denninger
Interferenz an der planparallelen Platte
4