Experiment

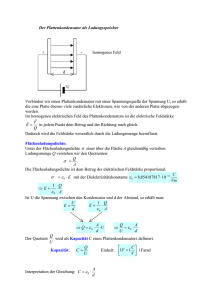
Kapazität eines
Plattenkondensators
Experimentelle Untersuchung des Abhängigkeit der
Kapazität eines Plattenkondensators vom Medium
zwischen der beiden Kondensatorplatten.
Projektwoche, Physik-LK
Hr. Legleitner
Q1-k, 22.09.2011
Mareike Krieger
Guido Sikora
Kai Oertel
Nora Gerhard
1. Problemstellung:
In diesem Experiment möchten wir die Abhängigkeit des Plattenkondensators
gegenüber dem Medium zwischen den beiden Kondensatorplatten
herausarbeiten.
2. Messprinzip mit Skizze und Versuchsablauf:
Benötigte Materialien:
- Hochspannungsgerät
- Spannungsmessgerät
- Plattenkondensator
- Messverstärker
- Voltmeter
- zwei Vektorkugeln
- Plastikabstandhalter
Versuchsaufbau :
Vor dem eigentlichen Experiment zur Kapazität eines Plattenkondensators
müssen wir ein Vorexperiment durchführen, welches uns helfen soll den
Sachverhalt besser zu verstehen und nachvollziehen zu können.
Hierzu benötigen wir zusätzlich zu den oben aufgeführten Materialien eine
Kunststoffplatte. Außerdem benötigen wir anstatt eines normalen
Kondensators einen mit runden Platten und die beiden Vektorkugeln und die
Plastikabstandhalter fallen weg. Zur Durchführung des Experimentes wird
nun das Hochspannungsnetzgerät mit dem Plattenkondensator verbunden
und auf eine Spannung von 2-5kV eingestellt. Das Voltmeter soll die
Spannung zwischen den beiden Platten messen. Im weiteren Verlauf wird
nun das Hochspannungsnetzgerät von dem Kondensator getrennt und eine
Kunststoffplatte wird zwischen die Platten geschoben.
Unsere Vermutung vor dem Durchführen des Experimentes war, dass die
Spannung sich von dem Einschieben der Kunststoffplatte beeinflussen lässt
und zwar soweit, dass sich die Spannungen verringert. Dies geschieht
deshalb, weil die Kunststoffplatte im Gegensatz zur positiven
Kondensatorplatte negativ geladen ist. Die Feldlinien des elektrischen Feldes
laufen also nicht mehr von einer Kondensatorplatte zur anderen, sondern von
der positiven Platte zur Kunststoffplatte, also ist zwischen den beiden Platten
keine Spannung mehr zu messen.
Skizze zum Versuchsaufbau
Zu beobachten war bei diesem Vorexperiment, dass die Spannung zwischen
den Platten nach dem Trennen von dem Hochspannungsnetzgerät erst
konstant blieb. Als wir dann die Kunststoffplatte einschoben, sank die
Spannung und als wir sie wieder entfernten stieg die angezeigte Spannung
zwischen den Platten wieder.
Nun steigen wir nach dem Vorexperiment in das Hauptexperiment ein. Dazu
bauen wir anstatt einen runden Plattenkondensator einen eckigen in den
Stromkreis ein und verwenden außerdem auch die beiden Vektorkugeln,
welche im Vorexperiment nicht benötigt wurden. Eine Schaltskizze zu dem
Versuchsaufbau findet sich hier, ebenso wie Bilder des Aufbaus.
Skizze zum Versuchsaufbau
Bilder zum Versuchsaufbau
Um
den
Versu
ch
korre
kt
durch
zufüh
ren
und
ausw
erten
zu
könn
en,
müss
en
mehrere Messwerte erhoben werden. Uns wurde eine Anzahl von acht
Messwerten vorgegeben. Wichtig ist hierbei noch zu wissen, das bei diesem
Experiment die anliegende Spannung des Hochspannungsnetzgerätes und
das Medium variiert wird, d.h. der Versuch wird in dem Medium Luft und in
dem Medium Isolator durchgeführt und zu jedem Medium wird eine
Messreihe mit jeweils nur 5 Messwerten erhoben, da eine Erhebung von 8
Messwerten nicht möglich ist (Erklärung siehe Fehleranalyse). Der Abstand
der Kondensatorplatten zwischen den Kondensatorplatten verändert sich
nicht!
Bei der Durchführung wird nun das Hochspannungsnetzgerät auf eine
bestimmte Spannung eingestellt. Mit Hilfe der Vektorkugel A wird nun Ladung
auf die Platten übertragen und gleich danach wird diese Ladung wieder mit
der Vektorkugel B von dieser Platte genommen. Danach wird der Ausschlag
des Voltmeters abgelesen, in die Messtabelle eingetragen und
ausgewertet.
Unsere Ausgangsvermutung haben wir vor dem Experiment wie folgt
formuliert: Die Spannung, welche mithilfe des Voltmeters zwischen den
beiden Kondensatorplatten gemessen wird, ist proportional zu der
anliegenden Spannung, welche mithilfe der Vektorkugeln auf den
Kondensator übertragen und danach wieder weggenommen wird. Auch wenn
wir das Medium Isolator verwenden, verhält sich die proportional.
Wenn wir aber nun das Medium verändern, vergrößert sich die Kapazität des
Kondensators, da sich das elektrische Feld verkleinert, durch die Einführung
der Kunststoffplatte.
4. Formeln
C=Q/U
Die Kapazität eines Kondensators ist der Quotient aus der Ladung der
Platten und der Spannung.
Q=σ*A
Die Ladung der Platten kann man mithilfe der Oberflächenladungsdichte und
der Fläche der Platten berechnet werden und ist das Produkt der beiden
Größen.
σ= ε0*E
Die Oberflächenladungsdichte ergibt sich aus der Konstanten ε0 = 8085*10ˉ¹²
und der elektrischen Feldstärke.
U=E*d
Die Spannung ist das Produkt der Feldstärke und des Abstandes der Platten.
→ Wenn man diese Formel nun in die erste aufgelistete Formel einsetzt
erhält man erst die Gleichung
C=(ợ*A)/(E*d)
C= (ε0*A)/d , da sich E wegkürzt.
5. Messwerte:
a) Kapazität im Medium Luft
Messvorgänge
1
2
3
4
5
Spalte 1:
Spalte 2:
Spalte 3:
Spalte 4:
d in m
0,01
0,01
0,01
0,01
0,01
U in V
1000
1500
2000
2500
3000
Q in C
80*10^-9
120*10^-9
160*10^-9
190*10^-9
230*10^-9
Die Versuchsvorgänge werden nummeriert.
Der Plattenabstand bleibt konstant.
Die Spannung wird von und je um 500V erhöht.
Die Ladung der Platten wird abgelesen.
b) Kapazität im Medium Isolator
Messvorgänge
1
2
3
4
5
Spalte
Spalte
Spalte
Spalte
1:
2:
3:
4:
d in m
0,01
0,01
0,01
0,01
0,01
U in V
1000
1500
2000
2500
3000
Q in C
170*10^-9
300*10^-9
430*10^-9
550*10^-9
610*10^-9
Die Versuchsvorgänge werden nummeriert.
Der Plattenabstand bleibt konstant.
Die Spannung wird von und je um 500V erhöht.
Die Ladung der Platten wird abgelesen.
6. Auswertung:
Bei der Auswertung dieses Experimentes wird die Kapazität des
Plattenkondensators mit Hilfe der Formel C=Q/U berechnet. Im Anschluss
wird aus den berechneten Werten ein Mittelwert gebildet, der die
durchschnittliche Kapazität des Plattenkondensators während des Versuches
angibt.
a) Kapazität im Medium Luft
Messvorgänge
1
2
3
4
5
C in C/V
8*10^-11
8*10^-11
8*10^-11
7,6*10^-11
7,67*10^-11
C = 80*10^-9/ 1000
Mittelwert 7,854*10^-11
Spalte 1: Die Versuchsvorgänge werden nummeriert.
Spalte 2: Die Kapazität ist der Quotient aus der
gemessenen Ladung und der gegebenen Spannung.
Zeile 6: Der Mittelwert ist der Quotient aus der Summe aller
Kapazitäten geteilt durch die Anzahl der Messvorgänge.
b) Kapazität im Medium Isolator
Messvorgänge
1
2
3
4
5
C in C/V
1,7*10^-10
2*10^-10
2,15*10^-10
2,2*10^-10
2,03*10^-10
C =170*10^-9/ 1000
Mittelwert 2,016*10^-10
Spalte 1: Die Versuchsvorgänge werden nummeriert.
Spalte 2: Die Kapazität ist der Quotient aus der
gemessenen Ladung und der gegebenen Spannung.
Zeile 6: Der Mittelwert ist der Quotient aus der Summe aller
Kapazitäten geteilt durch die Anzahl der Messvorgänge.
Die graphische Auswertung des Versuches sieht wie folgt aus:
Kapazität eines Plattenkondensators
in verschiedenen Medien
0
0
a) Kapazität im Medium Luft
Lineare Regression für a)
Kapazität im Medium Luft
b) Kapazität im Medium
Isolator
Lineare Regression für b)
Kapazität im Medium Isolator
Ladung in C
0
0
0
0
0
0
0
500
1000 1500 2000 2500 3000 3500
Spannung in V
Aus unseren Messergebnissen geht hervor, dass sich die Ladung des
Plattenkondensators proportional zur Spannung verhält. Außerdem wird vor
allem in der graphischen Auswertung deutlich, dass die Kapazität des
Plattenkondensators im Medium Isolator größer ist als die Kapazität im
Medium Luft.
7. Fehleranalyse:
Um Fehlerquellen analysieren und benennen zu können, muss man in den
meisten Fällen den relativen prozentualen Messfehler bestimmen.
Diesen relativen Messfehler errechnet man, indem man, in diesem Fall, den
den Betrag aus der Differenz der Kapazität und des Mittelwertes der
Kapazität durch den Mittelwert teilt. Diesen Quotienten muss man dann noch
mit 100 multiplizieren, damit man auf die gewünschte Prozentzahl kommt.
a) Kapazität im Medium Luft
Messvorgänge Relativer Fehler
1
1,859%
2
1,859%
3
1,859%
4
3,234%
5
2,343%
Spalte 1: Die Versuchsvorgänge werden nummeriert.
Spalte 2: Der relative Messfehler wird berechnet.
b) Kapazität im Medium Isolator
Messvorgänge Relativer Fehler
1
15,675%
2
0,794%
3
6,647%
4
9,127%
5
0,694%
Spalte 1: Die Versuchsvorgänge werden nummeriert.
Spalte 2: Der relative Messfehler wird berechnet.
An diesen relativen prozentualen Messfehlern lässt sich nun gut erkennen,
bei welchen Messvorgängen sorgfältig und korrekt gemessen wurden und bei
welchen weniger.
Im Allgemeinen lässt sich sagen, dass hier, wie bei jedem Experiment,
Messfehler durch unterschiedliche Umwelteinflüsse entstehen können. Nur
das Öffnen eines Fenstern verändert diese Einflüsse und die Gegebenheiten,
welche bei der vorherigen Durchführung vorhanden waren.
8. Zusammenfassung:
Zusammenfassend lässt sich sagen, dass wir unsere anfänglich Vermutung
verifizieren können und die Problemstellung bearbeitet haben. In zwei
Skizzen lässt sich der Zusammenhang zwischen der Kapazität und dem
Medium gut darstellen.
Skizze 1: Medium Luft
Hier ist zu erkennen, dass die Feldlinien ohne Unterbrechung von der
positiven Kondensatorplatte zur negativen Kondensatorplatte laufen. Die
Kapazität zwischen den beiden Platten ist also überall, je nach anliegender
Spannung, gleich.
Skizze 2: Medium Isolator
Aus dieser Skizze wird deutlich, dass sich das elektrische Feld E bei der
Einführung eines Isolators verändert. Auf Grund der elektrischen Polarisation
werden die Feldlinien weniger. Diese Abnahme der Feldliniendichte verringert
das elektrische Feld. Aus der Formel C=(ợ*A)/(E*d) geht hervor, dass die
Kapazität antiproportional zur elektrischen Feldstärke ist. Aus diesem Grund
wird die Kapazität größer, wenn man einen Isolator als Medium einsetzt, da
sich die elektrische Feldstärke verringert.