Kathetensatz

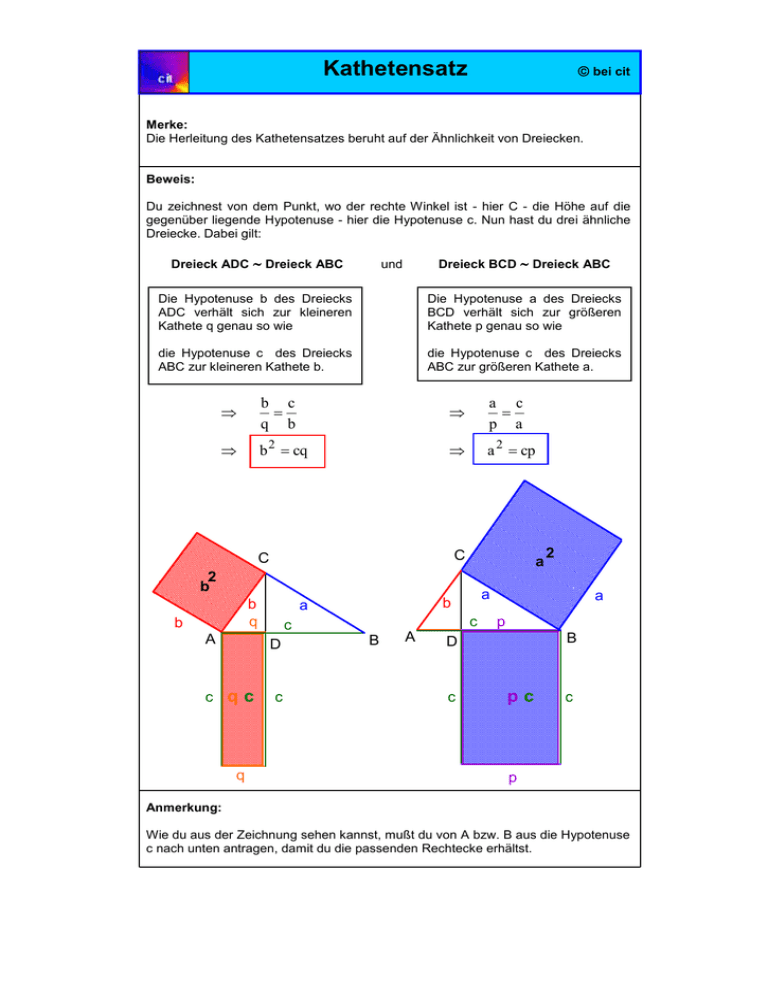
Kathetensatz
bei cit
Merke:
Die Herleitung des Kathetensatzes beruht auf der Ähnlichkeit von Dreiecken.
Beweis:
Du zeichnest von dem Punkt, wo der rechte Winkel ist - hier C - die Höhe auf die
gegenüber liegende Hypotenuse - hier die Hypotenuse c. Nun hast du drei ähnliche
Dreiecke. Dabei gilt:
Dreieck ADC Dreieck ABC
Dreieck BCD Dreieck ABC
und
Die Hypotenuse b des Dreiecks
ADC verhält sich zur kleineren
Kathete q genau so wie
Die Hypotenuse a des Dreiecks
BCD verhält sich zur größeren
Kathete p genau so wie
die Hypotenuse c des Dreiecks
ABC zur kleineren Kathete b.
die Hypotenuse c des Dreiecks
ABC zur größeren Kathete a.

b c

q b

a c

p a

b 2  cq

a 2  cp
C
C
a
2
b
b
q
b
A
c qc
q
c
c
D
c
a
b
a
B
A
a
p
B
D
c
2
pc
c
p
Anmerkung:
Wie du aus der Zeichnung sehen kannst, mußt du von A bzw. B aus die Hypotenuse
c nach unten antragen, damit du die passenden Rechtecke erhältst.