Dreieck / Viereck / Linearkombination Gegeben sind die drei Punkte

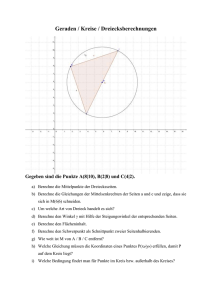
Dreieck / Viereck / Linearkombination
Gegeben sind die drei Punkte A(2|1|4), B(3|4|5) und C(1|4|3).
Berechne die Seiten, die Winkel des Dreiecks; ermittle, welche besondere Form das Dreieck hat und
berechne seinen Flächeninhalt.
Mit dem Punkt D(1|16|3) soll das Dreieck zu einem Viereck ergänzt werden; es ist ein ebenes
⃗⃗⃗⃗⃗ = 𝑥 ∙ 𝐴𝐵
⃗⃗⃗⃗⃗ + 𝑦 ∙ 𝐴𝐶
⃗⃗⃗⃗⃗ möglich ist. Überprüfe das.
Viereck, wenn die Linearkombination 𝐴𝐷
Berechne dann den Diagonalenschnittpunkt.
Bewegungsaufgabe
2
3
Ein Schiff S1 fährt auf der Route 𝑔: 𝑥 = ( ) + 𝑡 ∙ ( ), ein weiteres S2 auf der Route
3
6
11
2
h: 𝑥 = ( ) + 𝑡 ∙ ( ) [Koordinaten in km, t in Stunden].
8
−5
Berechne die Geschwindigkeit der Schiffe, ihre Position nach 2 Stunden, den möglichen Treffpunkt
der Schiffe, wenn eins wartet, sowie die kürzeste Entfernung, wenn beide mit konstanter Fahrt
fahren.
Dreieck / Viereck / Linearkombination
Gegeben sind die drei Punkte A(2|1|4), B(3|4|5) und C(1|4|3).
Berechne die Seiten, die Winkel des Dreiecks; ermittle, welche besondere Form das Dreieck hat und
berechne seinen Flächeninhalt.
Mit dem Punkt D(1|16|3) soll das Dreieck zu einem Viereck ergänzt werden; es ist ein ebenes
Viereck, wenn die Linearkombination ⃗⃗⃗⃗⃗
𝐴𝐷 = 𝑥 ∙ ⃗⃗⃗⃗⃗
𝐴𝐵 + 𝑦 ∙ ⃗⃗⃗⃗⃗
𝐴𝐶 möglich ist. Überprüfe das.
Berechne dann den Diagonalenschnittpunkt.
Bewegungsaufgabe
2
3
Ein Schiff S1 fährt auf der Route 𝑔: 𝑥 = ( ) + 𝑡 ∙ ( ), ein weiteres S2 auf der Route
3
6
11
2
h: 𝑥 = ( ) + 𝑡 ∙ ( ) [Koordinaten in km, t in Stunden].
8
−5
Berechne die Geschwindigkeit der Schiffe, ihre Position nach 2 Stunden, den möglichen Treffpunkt
der Schiffe, wenn eins wartet, sowie die kürzeste Entfernung, wenn beide mit konstanter Fahrt
fahren.
Lösungen:
Das Dreieck ist gleichschenklig, AB = AC = 3,32, BC = 2,83, M(2|4|4), h=3, A = 4,25.
⃗⃗⃗⃗⃗
𝐴𝐷 = 2 ∙ ⃗⃗⃗⃗⃗
𝐴𝐵 + 3 ∙ ⃗⃗⃗⃗⃗
𝐴𝐶 , damit lässt sich der erste Vektor aus den anderen beiden konstruieren, liegt
also in der gleichen Ebene.
2
−1
3
−2
Die Diagonalen sind 𝑔𝐴𝐷 : 𝑥 = (1) + 𝑡 ∙ ( 15 ) 𝑢𝑛𝑑 𝑔𝐵𝐶 : 𝑥 = (4) + 𝑠 ∙ ( 0 ); sie schneiden sich für
4
−1
5
−2
s = 0,6 und t = 0,2 in S(1,8|4|3,8).
SCHIFFE:
Das Schiff S1 fährt mit √3² + 6² = 6,71 [km/h], das Schiff S2 mit 5,39 km/h.
Ersetzt man in der ersten Gleichung t durch s, so treffen sich die Routen mit s = 55/27 und t = -13/9 in
P(8,11|15,22); hier hätte das 2. Schiff dann schon vor 13/9 h = 1h 27min halten müssen, das andere
kommt dort erst 55/27h nach Beobachtungsbeginn dort an, also gut 2 Stunden (von t=0 an
gemessen).
2 + 3𝑡
−9 + 𝑡
11 + 2𝑡
Der Verbindungsvektor der Schiffe zum Zeitpunkt t ist (
)−(
)=(
),
3 + 6𝑡
−5 + 11𝑡
8 − 5𝑡
seine Länge ist d(t) = √(−9 + 𝑡)2 + (−5 + 11𝑡)²,
daher muss der Radikand
r(t) = (−9 + 𝑡)2 + (−5 + 11𝑡)² = 81 – 18t + t² + 25 - 110t +121t² = 106 - 128t +122t²,
r‘(t) = 244t – 128 hat die Nullstelle bei 128/244 = 32/61, r(t) als oben offene Parabel also hier sein
Minimum, d(32/61) = 8,51; knapp 0,5 Stunden nach Beobachtungsbeginn beträgt die minimale
Entfernung der Schiffe 8,51km!