Die Ratte im Labyrinth | Repr asentation und Lernen aus

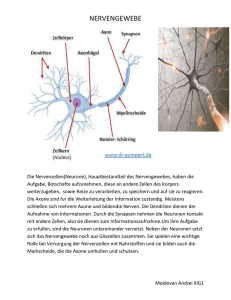
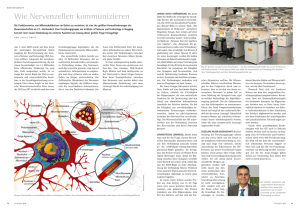
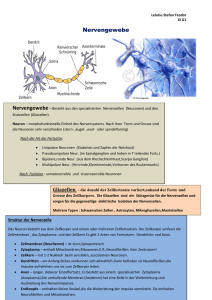
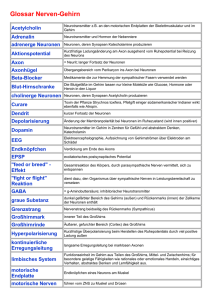
Die Ratte im Labyrinth | Reprasentation und
Lernen aus neurowissenschaftlicher Sicht
Christian W. Eurich
Institut fur Theoretische Neurophysik, Universitat Bremen,
Kufsteiner Str., D-28359 Bremen
[email protected]
In den letzten Jahren sind in den experimentellen und theoretischen Neurowissenschaften erhebliche Fortschritte auf den Gebieten der Signalverarbeitung durch Nervenzellverbande und der
Plastizitat im Nervensystem in Verbindung mit Lernen erzielt
worden.
So lat sich die Reprasentation sensorischer oder motorischer
Signale durch Gruppen von Neuronen mittels der statistischen
Schatztheorie quantitativ charakterisieren. Ein Ansatz besteht
darin, ein Versuchstier einer Reizsituation auszusetzen und aus
den neuronalen Antworten den Reiz zu rekonstruieren. Beispielsweise kann durch Messung und Analyse der Antworten von Nervenzellen im Hippocampus einer Ratte rekonstruiert werden, in
welchem Teil seiner Umgebung sich das Tier jeweils aufhalt. Derartige Methoden geben Hinweise auf allgemeine Prinzipien neuronaler Signalverarbeitung und erlauben Ruckschlusse auf die Art
des verwendeten Codes.
Auf dem Gebiet der Plastizitat lassen sich prazise Bedingungen fur den Signalu auf zellularer und subzellularer Ebene angeben, unter denen sich synaptische U bertragungseigenschaften
selbstorganisiert andern (Hebbsches Lernen). Obendrein ist erst
in jungster Zeit nachgewiesen worden, da die Hebbsche Plastizitat tatsachlich mit Lernvorgangen einhergeht.
1
Einleitung
Im folgenden sollen schlaglichtartig
Dendriten
zwei wichtige Entwicklungen in den
Neurowissenschaften beschrieben werZellkern
den: Das Studium der Verarbeitung
von sensorischen Reizen durch Ner- Soma
venzellverbande und die Charakterisierung selbstorganisierter Hebbscher Plastizitat. Dabei wird besonderer Wert
Axon
auf die Frage gelegt, wie Theorie und
MyelinExperiment ineinandergreifen, um zu
hülle
einem Verstandnis wesentlicher Prinzipien zentralnervoser Signalverarbeitung
Axonale
zu gelangen.
Endigungen
In Kapitel 2 werden einige Grundlagen der Neurobiologie wiederholt und
gangige Modelle von Nervenzellen beschrieben. Kapitel 3 beschaftigt sich
mit der Reprasentation von Reizen
durch Gruppen von Nervenzellen. Kapitel 4 schlielich behandelt neue Aspekte Abbildung 1: Schematische Darstellung
Hebbschen Lernens.
eines biologischen Neurons. Abbildung
aus [6].
2
Grundlagen der
Neurobiologie und
neuronale Modelle
Die Nervenzelle. Biologische Ner-
venzellen (Neuronen ) dienen der Aufnahme, Verarbeitung und Weiterleitung
von Signalen (Abbildungen 1 und 2).
Diese Signale haben die Form raumzeitlicher Spannungsanderungen (Potentialanderungen ) uber der Zellmembran.
Im Ruhezustand ist das Zellinnere negativ gegenuber dem Auenraum, und
die Spannung betragt ca. ;70 mV (sogenanntes Ruhepotential ).
Die Dendriten stellen die Eingangsfasern des Neurons dar. Sie sind be-
setzt mit bis zu 105 Kontaktstellen, den
Synapsen, uber die das Neuron Signale von anderen Nervenzellen empfangt.
Die Signale breiten sich im Dendritenbaum und bis zum Zellkorper (Soma )
aus. U berschreitet durch Depolarisation
der Membran die Spannung am Soma
einen Schwellenwert von ca. ;40 mV, so
wird am Ansatzpunkt der Nervenfaser
(dem Axonhugel ) eine pulsformige elektrische Welle (Aktionspotential , Spike )
ausgelost, die entlang der Nervenfaser
(Axon ) zu den axonalen Endigungen
lauft: das Neuron feuert . Zur Erhohung
der Signalgeschwindigkeit sind manche
Axone von einer isolierenden Proteinschicht, der Myelinhulle , umgeben. An
Wird eine Nervenzelle erregt, so
antwortet sie im allgemeinen mit einer Serie von Aktionspotentialen, einem Spiketrain ; Abbildung 3 zeigt ein
Beispiel. Der Abstand zweier Spikes
kann dabei nicht beliebig klein sein,
da die Zelle nach der Erzeugung eines Spikes fur eine kurze Zeit, die Refraktarzeit , in eine Regenerationsphase
geht. Spiketrains wie der in Abbildung
Abbildung 2: Querschnitt durch das
Mittelhirn eines Schleuderzungensalamanders. Einige Nervenzellen sind
schwarz angefarbt; diese Nervenzellen
Zeit
reagieren auf visuelle Eingaben und
projizieren in den Hirnstamm, wo sie
nachgeschaltete Nervenzellen erregen, Abbildung 3: Spiketrain eines Mitteldie die am Beutefang beteiligten Mus- hirnneurons eines Salamanders als Antkeln ansteuern. Foto: U. Dicke.
wort auf ein schwarzes bewegtes Rechteck, das dem Tier prasentiert wird.
Die Aktionspotentiale sind als Striche
den axonalen Endigungen schlielich dargestellt. Skala: 500 ms. Daten mit
wird das elektrische Signal uber Synap- freundlicher Genehmigung von B. Liensen an nachgeschaltete Neuronen oder stadt. Abbildung aus [6].
Muskelfasern ubertragen.
Die synaptische Signalubertragung 3 gezeigte werden gemessen, indem eine
erfolgt entweder durch direkte elektri- Meelektrode entweder in das Nervensche Kopplung oder auf chemischem zellgewebe zwischen die Neuronen geWege. Bei der chemischen Synapse be- setzt oder in eine Nervenzelle eingestowirkt ein ankommendes Aktionspoten- chen wird (extrazellulare bzw. intrazeltial in der vorgeschalteten Zelle die lulare Ableitung ). Mit einer EinzelelekAusschuttung von Transmitterstoen, trode kann die Aktivitat einzelner oder
die zur nachgeschalteten Zelle diundie- mehrerer Neuronen aufgezeichnet werren und dort aufgenommen werden. Als den. In den letzten Jahren werden verFolge davon kommt es in der nachge- mehrt Multielektroden verwendet, um
schalteten Zelle zu einer A nderung der gleichzeitig die Aktivitat vieler NervenMembranspannung, zu einem postsyn- zellen zu registrieren und auf diese Weiaptischen Potential . Chemische Syn- se Aussagen uber die gemeinsame Verapsen konnen erregend (exzitatorisch ) arbeitung von Signalen zu treen.
oder hemmend (inhibitorisch ) wirken,
je nach Vorzeichen des postsynapti- Neuronenmodelle. Fur das Studium neuronaler Netze und die Modelschen Potentials.
lierung biologischer Nervennetze wird
unterschiedlich stark von den komplexen Eigenschaften biologischer Neuronen abstrahiert.
In Netzen mit diskreter Zeitstruktur
verwendet man das in Abbildung 4 dargestellte, stark vereinfachte Neuronenmodell. Das Neuron bekommt Eingaben
y1
y2
w2
w1
S
wn
yn
f
Feuerrate f
y
ymax (b)
0
h0
Aktivierung h
Abbildung 4: Modellneuron fur Netze
mit zeitdiskreter Dynamik. f ist das
Symbol fur die Ausgabefunktion.
y1 ; : : : ; yn, die entweder von anderen
Neuronen stammen oder auere Eingaben in das Netzwerk darstellen. Die
Eingaben werden durch Multiplikation
mit den Synapsenstarken w1; : : : ; wn gewichtet. Die Aktivierung h des Neurons
betragt
n
X
h = wi yi :
i=1
Fur wi > 0 wirkt die Eingabe yi des
vorgeschalteten Neurons i exzitatorisch,
fur wi < 0 inhibitorisch (i = 1; : : : ; n).
Die Ausgabe y des Neurons wird durch
Anwendung einer Ausgabefunktion f
berechnet: y = f (h). Im einfachsten Fall, dem sog. McCulloch-PittsNeuron , sind die Eingaben und die
Ausgabe binar (y1; : : : ; yn; y 2 f0; 1g)
und werden als "Feuern\ bzw. "NichtFeuern\ interpretiert. Fur McCullochPitts-Neuronen stellt f die HeavisideFunktion dar,
f (h) = (h ; 0 ) ;
wobei 0 der Schwellenwert fur das
Feuern des Neurons ist. Nehmen die
y1 ; : : : ; yn ; y kontinuierliche Werte an,
spricht man von einem Analogneuron ,
und die Ausgabe y wird als mittlere Anzahl von Spikes interpretiert, die das
Neuron pro Zeiteinheit erzeugt (Feuerrate ). Fur Analogneuronen verwendet man eine sigmoide Ausgabefunktion, d.h. eine stetige und monotone
Funktion, die von Null auf einen Maximalwert ymax ansteigt. Als Beispiel sei
die Fermi-Funktion
ymax
f (h) =
(1)
1 + e;(h;h0 )
genannt, wobei h0 die Aktivierung angibt, bei der das Neuron mit der Rate
ymax=2 feuert (Abb. 4).
Das gebrauchlichste Neuronenmodell
fur Netzwerke mit zeitkontinuierlicher
Dynamik ist das Integrate-and-FireNeuron . Die dynamische Variable ist
das Membranpotential V = V (t), wobei das Ruhepotential zumeist auf Null
gesetzt wird. Abbildung 5 zeigt das Ersatzschaltbild des Neurons, das gultig
ist, solange das Membranpotential so
klein ist, da das Neuron nicht feuert.
R ist der Widerstand und C die Kapa-
C
R
V(t)
I(t)
nenmodelle, die die raumliche Struktur des in Abb. 1 dargestellten Neurons
berucksichtigen. Zur Simulation groerer Netzwerke verwendet man wegen
des geringeren Rechenaufwandes jedoch
zumeist die genannten einfacheren Modelle.
Das Gehirn. Das menschliche Ge-
hirn besteht aus mehr als 200 Milliarden
Abbildung 5: Ersatzschaltbild fur ein Nervenzellen, und im Durchschnitt hat
Integrate-and-Fire-Neuron unterhalb jedes Neuron 1000 Kontaktstellen (Synder Feuerschwelle.
apsen) mit anderen Neuronen. Eine eingehendere Beschreibung des Gehirns,
zitat der Zellmembran; die Stromquelle seiner Anatomie und Physiologie wurde
I (t) modelliert die Eingabe des Neurons den Rahmen dieses Beitrags bei weiaufgrund der Spikeaktivitaten der ande- tem sprengen; stattdessen sei auf einen
ren Neuronen im Netzwerk. Fur V < 0 Punkt hingewiesen, der die Komplexitat
gilt die lineare Gleichung
der neuronalen Verarbeitung verdeutlichen soll. Die klassische Sicht auf die
dV V
C + = I (t)
Signalverarbeitung im Gehirn ist in Abdt R
bildung 6 dargestellt. Demnach ist der
mit einer Anfangsbedingung V (t0 ) =
V0 . Erreicht das Membranpotential zu
einer Zeit t1 eine Feuerschwelle 0 ,
sensorische Eingaben
V (t1 ) = 0 , so gibt das Neuron
einen Spike ab, der selber nicht modelliert wird, und das Membranpotential
wird auf Null gesetzt: limt!t+1 V (t) =
interne Verarbeitung
0. Refraktarzeiten konnen durch eine zeitabhangige Feuerschwelle, 0 =
0 (t), berucksichtigt werden. Fur die
auftretenden Strome I (t) wahlt man
Motorische Reaktionen
gema dem Pulscharakter der Spikes
die Delta-Funktion, oder man berucksichtigt postsynaptische Potentiale in
Form einer Alpha-Funktion :
Abbildung 6: Schematische Darstellung
der herkommlichen Sicht auf die SignalI (t) = ce;t ; > 0
verarbeitung im Nervensystem.
mit c > 0 fur Exzitation und c < 0 fur
Inhibition.
Signalu im Nervensystem im wesentNeben den beschriebenen gibt es wei- lichen folgendermaen charakterisiert:
tere, insbesondere komplexere Neuro- Durch unsere Sinnesorgane bekommen
?
wir sensorische (visuelle, auditorische
usw.) Eingaben; diese werden intern
verarbeitet und resultieren schlielich in
einer Antwort in Form von motorischer
Aktivitat. An dieser Sichtweise sind
zwei Punkte irrefuhrend: Erstens wird
der Einu der sensorischen Eingaben
auf die zentralnervose Aktivitat uberbetont. Zweitens ist die mittlere Stufe
der internen Verarbeitung nicht naher
speziziert und suggeriert damit insgesamt eine im wesentlichen vorwartsgerichtete Signalverarbeitung im Nervensystem. Zur Unterstreichung dieser
Aussagen zeigt Abbildung 7 ein von
Felleman und van Essen aus verschiedenen anatomischen Studien zusammengestelltes Diagramm von bis dato bekannten anatomischen Verbindungen innerhalb des visuellen Systems
von Primaten [11]. Jedes Kastchen entspricht einem Gehirnareal (zumeist in
der Grohirnrinde), in dem sich Neuronen benden, die auf visuelle Eingaben reagieren. Die Abbildung veranschaulicht, da die weitaus meisten
Nervenzellen (es sind uber 95%) keinen direkten Kontakt zur sensorischen
Oberache haben, sondern ihre Eingaben ausschlielich von anderen Nervenzellen bekommen. Gleiches gilt fur die
Schnittstelle zu den Muskeln: nur wenige Prozent der Nervenzellen erregen
nachgeschaltete Muskelfasern; die ubrigen geben ihre Signale an andere Nervenzellen weiter. Des weiteren ist das in
Abbildung 7 dargestellte System massiv ruckgekoppelt, was einer einfachen
Charakterisierung der Verhaltensweisen
und der Aufgaben der einzelnen Areale
entgegensteht.
Aus theoretischer Sicht kann man das
Gehirn somit als ein komplexes dyna-
Abbildung 7: Anatomische Verbindungen innerhalb des visuellen Systems eines Primaten. Abbildung nach [11].
misches System charakterisieren, dessen Aktivitat wesentlich seiner internen
Dynamik entspringt und das durch sensorische Eingaben (\Inputs\) lediglich
gestort wird. Dieses Bild ist deutlich
verschieden von der Vorstellung, da
das Gehirn mageblich dadurch zu charakterisieren sei, da es externe Signale
aufnimmt und verarbeitet.
3
Neuronale Repr
asentation
Wie im vorigen Abschnitt angedeutet,
sind im Nervensystem stets sehr viele
Neuronen aktiv, von denen ein groer
Anteil nicht in direktem Kontakt mit
den Umweltreizen steht. Eine auerst
komplexe Signalverarbeitung innerhalb
des Nervensystems geht einher mit der
bewuten oder unbewuten Wahrnehmung der Welt; wir sagen, die Umwelt
sei im Gehirn reprasentiert .
Diese Betrachtung fuhrt unmittelbar
zu der Frage nach der Gute der Reprasentation von Umweltreizen in einer Gruppe (Population ) von Neuronen. Ein experimenteller Zugang besteht darin, einem Tier Reize zu prasentieren und die durch Einzel- oder Multizellableitungen gewonnenen Antworten der Nervenzellen zu charakterisieren
und auf A quivalenz mit den Reizen zu
testen. Ein entsprechendes Vorgehen ist
auch auf der motorischen Seite moglich;
hier stellt sich die Frage nach der Beziehung zwischen den motorischen Aktionen des Organismus und einer entsprechenden Aktivitat von Nervenzellen, beispielsweise im Motorcortex.
Ein geeignetes Werkzeug zur Bestimmung der A quivalenz von neuronaler Aktivitat und sensorischen bzw.
motorischen Signalen ist die informationstheoretische Methode : der klassische Informationsbegri nach Shannon
(die Transinformation) quantiziert die
U bereinstimmung zweier Wahrscheinlichkeitsverteilungen; in diesem Fall
handelt es sich um die Verteilung der
dargebotenen Reize und die Verteilung
der Antworten der Neuronenpopulation. Als Standardwerk fur diese Methode sei das Buch von Rieke et al. [17]
empfohlen.
Eine alternative Methode der Datenauswertung besteht darin, mit Hilfe der Signale der Neuronenpopulation den Reiz zu rekonstruieren oder
mehrere Reize zu diskriminieren. Bei
der Rekonstruktion wird ublicherwei-
se der Schatzfehler ermittelt, der sich
aufgrund der beschrankten Anzahl der
beteiligten Neuronen oder der Stochastizitat der Neuronenantwort ergibt.
Die Schatzung eines Reizes mu hinreichend genau sein, um dem Organismus
ein adaquates Agieren und Reagieren
zu ermoglichen. Eine Methode, die sehr
gute Ergebnisse erzielt, ist die Rekonstruktion mittels Bayesscher Schatzverfahren ; diese wird im nachsten Abschnitt naher erlautert und anschlieend auf die Selbstlokalisation einer
Ratte in einem Labyrinth angewendet.
Bayessche Rekonstruktion. Gege-
ben seien N Neuronen, die auf die
Prasentation eines Reizes reagieren, der
sich an einer Stelle x in einem Reizraum
X bendet. Es kann sich bei x beispielsweise um einen Winkel im Ortsraum, eine Frequenz auf der Frequenzachse oder
die Orientierung eines Balkes im Intervall [0; 180] handeln. Der Einfachheit
halber wird X hier als eindimensional
angenommen, und die moglichen Reize
x aus X nehmen kontinuierliche Werte
an.
Gemessen werden die Spikezahlen
k1 ; : : : ; kN , die in einem Zeitintervall nach Prasentation des Reizes x in der
Population auftreten. Durch wiederholte Darbietung des Reizes gewinnt man
eine Verteilung der Spikezahlen, die sich
als bedingte Wahrscheinlichkeit schreiben lat: P (k1; : : : kN jx). Liegt diese
Verteilung vor, so kann man mittels einer Einzelmessung, die die Spikezahlen
k1 ; : : : ; kN zum Ergebnis habe, den Reizort abschatzen.
Fur diese Schatzung wird die
bedingte
Wahrscheinlichkeitsdich-
te p(xjk1; : : : kN ) benotigt, also die
Wahrscheinlichkeitsdichte dafur, da
sich der Reiz am Ort x bendet,
wenn bei einmaliger Prasentation
in der Population k1; : : : ; kN Spikes
gezahlt werden. P (k1; : : : kN jx) und
p(xjk1 ; : : : kN ) hangen uber den Satz
von Bayes zusammen:
P (k1; : : : kN jx)p(x)
p(xjk1 ; : : : kN ) =
:
P (k1; : : : ; kN )
(2)
p(x) beschreibt die Haugkeitsverteilung fur das Auftreten des Reizes am Ort x; diese Groe ist unabhangig vom neuronalen System und
wird als A-Priori-Wahrscheinlichkeit
(engl. prior ) bezeichnet. Sie wird
vom Experimentator vorgegeben oder
entspricht einer naturlichen Statistik
des Auftretens der Reize. Man nennt
p(xjk1 ; : : : kN ) entsprechend die APosteriori-Wahrscheinlichkeit , da sie
die Verteilung von x nach der Messung
des neuronalen Systems darstellt. Der
Nenner P (k1; : : : ; kN ) in Gleichung (2)
hat die Bedeutung einer Normierung
und kann uber den Satz von der totalen
Wahrscheinlichkeit berechnet werden:
P (k1 ; : : : ; kN ) =
R
P (k1; : : : ; kN jx)p(x) dx : (3)
X
Mittels eines geeigneten Verfahrens
mu zuletzt ein geschatzter Ort x^
aus der A-Posteriori-Verteilung ermittelt werden. Der optimale Schatzwert
(im Sinne eines quadratischen Fehlers) ist der Mittelwert der A-PosterioriVerteilung [14]. Da dieser zumeist nur
unter groem Rechenaufwand ermittelt werden kann, wird der aufgrund
der Messung geschatzte Ort x^ ublicherweise als die Stelle gewahlt, an der
p(xjk1 ; : : : kN ) maximal ist:
x^ = argmaxx2X p(xjk1 ; : : : ; kN ) : (4)
In der Regel wird es bei Experimenten aufgrund der begrenzten Mezeit nicht moglich sein, die Wahrscheinlichkeit P (k1; : : : kN jx) zu ermitteln, da
es sich i. a. um multivariate Verteilungen in hochdimensionalen Raumen handelt. In diesem Fall kann man unter
Zuhilfenahme von zusatzlichen Annahmen P (k1; : : : kN jx) aus einem Modell
bestimmen. Eine bei der Modellierung
haug verwendete Annahme ist, da die
Neuronen ihre Spikes unabhangig voneinander erzeugen. Mathematisch zerfallt P (k1; : : : kN jx) dann in ein Produkt
von Verteilungen fur die einzelnen Neuronen:
N
Y
P (k1; : : : kN jx) = P (kijx) : (5)
i=1
Zur Ermittlung der P (kijx) (i =
1; : : : ; N ) werden die mittleren Feuerraten fi (x), mit der das Neuron i auf
die Prasentation des Reizes x antwortet, als Funktion des Ortes x des Reizes gemessen. Man nennt fi (x) die Tuningkurve des i-ten Neurons. fi (x) ist
dann die im Zeitintervall im Mittel
erzeugte Anzahl von Spikes des Neurons i. Fur P (kijx) wahlt man nun eine
passende Statistik mit dem Mittelwert
fi (x). Das einfachste Modell beruht
auf der Annahme, da das Auftreten eines Spikes zu einer Zeit tj unabhangig
ist von den fruheren Spikezeitpunkten
tj ;1; tj ;2 ; : : : des Neurons; die Abfolge
von Spikes stellt dann einen PoissonProze dar. Die Wahrscheinlichkeit fur
das Auftreten von genau ki Spikes bei
Neuron i wahrend eines Beobachtungszeitraums betragt in diesem Fall
P (kijx) =
(fi(x))k e;f (x) :
ki !
i
i
(6)
Setzt man die Gleichungen (5) und
(6) in den Satz von Bayes (2) ein, so
lat sich der Ort des Reizes als Mittelwert der A-Posteriori-Verteilung oder
mit dem Kriterium (4) abschatzen.
Die Ratte im Labyrinth. Im Hip-
pocampus von Ratten existieren Zellen,
die aktiv werden, wenn sich der Kopf
des Tiers in einem bestimmten Raumbereich seiner Umwelt bendet; diese Raumbereiche werden Place Fields
genannt. Abbildung 8 zeigt die Place
Fields von 25 Zellen; diese sind symbolisch auf ein Labyrinth gelegt, durch das
die Ratte sich bewegt. Die Farbe kodiert
die Feuerrate, die das jeweilige Neuron
hat, wenn sich die Ratte am entsprechenden Ort bendet. Durch Registrierung des von einer Ratte in einem Labyrinth zuruckgelegten Weges und gleichzeitige Multizellableitungen lat sich
die Hypothese uberprufen, da die Aktivitat der Hippocampusneuronen hinreichend fur eine Selbstlokalisation der
Ratte in dem Labyrinth ist. Mit Hilfe der oben beschriebenen (und weiterer) Rekonstruktionsverfahren wird der
Weg der Ratte aus den Spikedaten von
25 Neuronen geschatzt und mit dem
tatsachlichen Weg verglichen.
Das Ergebnis einer Bayesschen Rekonstruktionen ist in Abb. 9 dargestellt.
Die obere Zeile zeigt den tatsachlichen
Weg und die dritte Zeile das Ergebnis
der Bayesschen Rekonstruktion, wie sie
im vorigen Abschnitt beschrieben wur-
Abbildung 8: Falschfarbendarstellung
von 25 Placeelds einer Ratte. Abbildung aus [21].
de. Als ein noch besseres Verfahren erweist sich eine Bayessche Rekonstruktion, die zwei Zeitschritte und eine Stetigkeit des Weges der Ratte einbezieht
(zweite Zeile). Die Resultate zeigen, da
eine kleine Population von Hippocampusneuronen hinreichend fur die Selbstlokalisation der Ratte in ihrem Labyrinth ist: bereits bei Berucksichtigung
von 25 Nervenzellen fallt die Genauigkeit der Rekonstruktion unter die Genauigkeit, mit der im Experiment die
tatsachliche Position der Ratte gemessen wurde.
Eine ernstzunehmende Kritik an
Bayesschen Rekonstruktionsverfahren
ist die Tatsache, da viel Vorwissen in
die Rekonstruktion eingeht: die Modalitat der Sensorik, die Dimensionalitat
des Reizes (d. h. die Anzahl der re-
Abbildung 9: Resultat der Bayesschen
Rekonstruktion. Die obere Zeile zeigt
die wahre Bahn der Ratte, die untere
Zeile die aus der Aktivitat von 25 Neuronen mittels des beschriebenen Verfahrens rekonstruierte Bahn. Die mittlere Zeile schlielich resultiert aus einem Bayesschen Verfahren, das jeweils
zwei aufeinanderfolgende Zeitabschnitte berucksichtigt und die Stetigkeit der
Bahn der Ratte voraussetzt. Abbildung
aus [21].
gistrierten Reizeigenschaften) usw. Eine "absolute\ Rekonstruktion neuronaler Aktivitat ohne jegliche Annahmen ist nicht moglich. Gema dieser
abgeschwachten Auassung kann man
Rekonstruktionsmethoden als (zumeist
einfache) mathematische Verfahren ansehen, die die simultane Aktivitat mehrerer Neuronen quantitativ charakterisieren.
Fisher-Information und neuronale Kodierungsstrategien. Bei Be-
ze fur den Fehler einer Rekonstruktion?
Die Antwort lautet ja; eine solche untere Grenze existiert, und sie ist i. a.
aufgrund der Stochastizitat der ausgewerteten Signale groer als Null. Interessant ist, da sich der minimal mogliche Fehler { ohne die Berucksichtigung
eines konkreten Rekonstruktionsverfahrens { berechnen lat, und zwar mit Hilfe der Fisher-Information .
Gegeben seien N Neuronen, die
bei wiederholter Prasentation eines
Reizes am Ort x im Reizraum X
mit einer Wahrscheinlichkeitsverteilung
P (k1; : : : ; kN ; x) reagieren. Aus einer
Einzelmessung der Spikezahlen der Population gewinnt man mit einem gegebenen Schatzverfahren S (beispielsweise der Bayesschen Methode) eine
Schatzung x^ fur x; bei T Messungen desselben Reizes die Schatzungen
x^1 ; : : : ; x^T . Als Bias bS des Schatzers
S bezeichnet man die mittlere Abweichung von wahrem und geschatztem
Ort:
T
X
1
b = lim
x^ ; x hx^ ; xi :
S
T ;!1 T t=1 t
(7)
Ein erwartungstreuer Schatzer (engl.
unbiased estimator ) ist ein Schatzer, fur
den bS = 0 gilt, der also im Mittel
den korrekten Ort liefert. Alle weiteren
U berlegungen dieses Abschnitts beziehen sich auf erwartungstreue Schatzer.
Der mittlere quadratische Fehler des
Schatzers S ist deniert als
T
1 P
(x)2 = lim
(x^ ; x)2
trachtung der rekonstruierten Wege in
Abb. 9 stellt sich die Frage, ob es nicht
T ;!1 T
t
weitere Rekonstruktionsmethoden gibt,
t=1
die aus dem Feuerverhalten der Neuro h(x^ ; x)2i :
(8)
nenpopulation den Weg der Ratte noch
besser schatzen konnen. Oder anders Die Fisher-Information der neuronaausgedruckt: gibt es eine untere Gren- len Population bzgl. des Reizes x ist de-
niert als
J (x) :=
*
!+
@ ln P (k1; : : : ; kN ; x) 2
@x
(9)
[14]; h: : :i bezeichnet wiederum den Erwartungswert uber die Wahrscheinlichkeitsverteilung P (k1; : : : ; kN ; x), und
ln : : : ist der naturliche Logarithmus.
Die Cramer-Rao-Ungleichung gibt
nun einen Zusammenhang zwischen der
Fisher-Information und dem mittleren
quadratischen Schatzfehler:
h(^x ; x)2 i J (1x) :
(10)
Gleichung (10) besagt, da der mittlere quadratische Fehler eines beliebigen erwartungstreuen Schatzers stets
groer oder gleich dem Kehrwert der
Fisher-Information ist. Das ist eine
weitreichende Aussage! Das Inverse der
Fisher-Information wird als minimaler Schatzfehler bezeichnet. Bei Vorliegen eines konkretes Schatzproblems hat
man stets zwei Dinge im Auge zu behalten: erstens konnen Schatzer mit Bias existieren, deren Fehler noch unterhalb des minimalen Schatzfehlers liegen. Zweitens ist es moglich, da samtliche Schatzer die untere Grenze der inversen Fisher-Information gar nicht erreichen, sondern stets daruber liegen.
Mit Hilfe der Fisher-Information (9)
und der Cramer-Rao-Ungleichung (10)
lassen sich nun Kodierungsstrategien
fur neuronale Populationen untersuchen (z. B. [16, 22, 9, 10]). Dabei stellt
sich die Frage, wie neuronale Populationen reagieren mussen, um eine
moglichst groe Fisher-Information, also einen moglichst kleinen minimalen
Schatzfehler, zu erzielen. Paradiso [16]
betrachtet ein Modell fur eine Population von Nervenzellen in einem visuellen Areal der Grohirnrinde und leitet
die Genauigkeit her, mit der die Orientierung von bewegten Balken reprasentiert ist. Zhang und Sejnowski [22]
beweisen, da identische Nervenzellen,
die unspezisch auf groe Bereiche im
Reizraum reagieren (beipielsweise groe
Place Fields wie die in Abbildung 8 gezeigten), ein hohes Auosungsvermogen
liefern, falls mehr als zwei Reizeigenschaften (Ort, Geschwindigkeit, Helligkeit usw.) kodiert werden. Eurich und
Wilke [9, 10] machen eine Reihe von
realistischeren Annahmen uber neuronale Populationen und ermitteln die
sich jeweils ergebende Reprasentationsgenauigkeit. Untersucht werden unter
anderem Populationen von Neuronen,
die eine Variabilitat in ihren Antworteigenschaften aufweisen, sowie verschiedene Arten der Korrelation in den Antworten der Neuronen. Es stellt sich dabei stets heraus, da gerade diejenigen
neuronalen Eigenschaften, die auch empirisch gefunden werden, eine genaue
Reprasentation von sensorischen Reizen
ermoglichen.
4
Hebbsches Lernen
Das Hebbsche Postulat. Im Jahre
1949 schlug der kanadische Psychologe
Donald Hebb in seinem richtungweisenden Buch "The Organization
of Behavior\ eine Hypothese uber
einen Mechanismus vor, wie Lernen
im Nervensystem auf zellularer Ebene
ablaufen konnte [13]:
"When an axon of cell A is near
enough to excite a cell B and
repeatedly or persistently takes part in firing it, some growth process or metabolic change
takes place in one or both cells
such that A's efficiency, as one
of the cells firing B, is increased.\
Die Hypothese beinhaltet zwei wesentliche Punkte: Erstens entsprechen
Lernprozesse anatomischen oder
physiologischen Veranderungen auf
zellularer oder subzellularer Ebene;
zweitens beruht diese Plastizitat auf
der Aktivitat der Nervenzellen und
ndet somit selbstorganisiert statt.
Demnach gibt es also dynamische Prozesse auf mindestens zwei Zeitskalen:
eine schnelle Dynamik der neuronalen
Erregung und Signalproduktion und
eine langsame Dynamik struktureller A nderungen. Bezuglich letzteren
erwahnt Hebb in seinem Buch die
Moglichkeit gerichteter Wachstumsbewegungen, konzentriert sich dann aber
auf den Vorschlag, da die Synapse der
Ort der plastischen A nderungen sei.
Obwohl es in den 40er Jahren noch
keine empirischen Hinweise auf die
Hypothese von Hebb gab, war sein
Buch der Auftakt fur ein gigantisches
neurowissenschaftliches Forschungsprogramm, das bis heute andauert.
LTP und LTD. Der Nachweis selbstorganisierter Plastizitat im Nervensystem begann in den 80er Jahren mit
der Entdeckung der Long-Term Potentiation (LTP) [3]. Es konnte nachgewiesen werden, da die gleichzeitige, wiederholte starke elektrische Reizung einer vor- und einer nachgeschalteten Zel-
le dazu fuhrt, da die nachfolgende Zelle uber langere Zeit hinweg starker auf
Reizung durch die vorgeschaltete Zelle reagiert, d. h. ein groeres postsynaptisches Potential entwickelt. Nachgewiesen wurde auch der umgekehrte Effekt der Long-Term Depression (LTD),
eine Abschwachung der Synapse, ebenfalls bedingt durch wiederholte gepaarte Reizung eines vor- und eines nachgeschalteten Neurons. LTP und LTD treten in vielen Hirngebieten auf, sind aber
im Hippocampus, einem Teil des Vorderhirns, besonders pronounciert. Der
Hippocampus steht vermutlich im Zusammenhang mit der Einspeicherung
neu erworbenen Wissens.
Auf theoretischer Seite wurden einfache, auf wechselseitiger Aktivitat von
Neuronen beruhende Lernregeln fur
neuronale Netze mit diskreter Zeitstruktur (t = 1; 2; : : :) entwickelt [4].
Die einfachste Variante solcher HebbRegeln lautet
wij (t + 1) = wij (t) + yj (t)hi (t) ; (11)
wobei wij (t) die Starke der Synapse ist,
mit der Neuron j zur Zeit t auf Neuron i einwirkt; stellt eine Lernrate
dar, hi ist die Aktivierung des nachgeschalteten Neurons i, und yj ist die
Feuerrate des vorgeschalteten Neurons
j . Die A nderung der Synapsenstarke
wij (t + 1) ; wij (t) ist proportional zum
Produkt yj hi. Ein Problem der Lernregel (11) besteht darin, da sie zu Instabilitaten in Netzwerken fuhrt: eine bereits groe Synapsenstarke bewirkt eine starke Aktivierung des nachgeschalteten Neurons und damit eine weitere Erhohung der Synapsenstarke. Abhilfe schaen hier eine Begrenzung des
Wertes von Synapsenstarken nach oben
oder die Einfuhrung einer Normierung
aller an einem Neuron sitzenden Synapsen; letzteres fuhrt zu einem Wettbewerb zwischen den Synapsen.
Zeitabhangiges Hebbsches Lernen
Seit 1994 sind auf dem Gebiet des
Hebbschen Lernens sowohl experimentell als auch theoretisch groe Fortschritte erzielt worden. Ein bis dato ungelostes Problem bezieht sich auf Lokalitat der Hebbschen Lernregel: die an
der Synapse beobachteten Veranderungen werden hervorgerufen aufgrund der
korrelierten Aktivitat des vor- und des
nachgeschalteten Neurons. Woher aber
wei \ die Synapse, da das nachge"schaltete
Neuron gefeuert hat? Es mu
ein Signal geben, da diese Information vom Axonhugel, wo die Aktionspotentiale entstehen, zur Synapse tragt.
In der Tat entdeckten Stuart und Sakmann 1994, da Aktionspotentiale nicht
nur entlang des Axons laufen wie bisher
angenommen, sondern auch in den Dendritenbaum zuruckpropagieren, wo sich
die meisten Synapsen benden [20]. Ein
solches ruckpropagierendes Aktionspotential ist ein perfekter Kandidat fur
das gesuchte Signal.
Die exakten zeitlichen Bedingungen
fur das Auftreten von LTP und LTD
wurden seit 1997 in der Reihe von Artikeln aufgeklart [15, 1, 23, 2]. Markram
et al. [15] wiesen nach, da eine
Verstarkung der Synapse durch LTP
stattndet, wenn die vorgeschaltete Zelle wenige Millisekunden vor der nachgeschalteten Zelle ein Aktionspotential produziert, wenn es also eine kausale Einwirkung der vor- auf die nachgeschaltete Zelle gibt. Ist hingegen das
Signal der vorgeschalteten Zelle verspatet, so ndet LTD statt: die zeitliche Korrelation der Signale kann in
diesem Fall nur zufallig sein. Die korrelierten Aktivitaten mussen innerhalb
eines Zeitraums von 100 ms stattnden, ansonsten ndet keine Veranderung statt. Bi et al. [1] und Zhang et
al. [23] schlielich haben die Starke von
LTP bzw. LTD als Funktion des zeitlichen Abstandes zwischen der Aktivitat
der vor- und der nachgeschalteten Zelle, das sog. Lernfenster , exakt vermessen (siehe Abbildung 10). Das Lernfenster zeigt, da die zeitliche Abfolge der
Aktionspotentiale im Nervensystem eine groe Rolle fur plastische Veranderungen spielt.
Eine komplexere neuronale Verschaltung wurde von Bi et al. [2] untersucht: Zwei Nervenzellen, die uber mehrere parallele Leitungen durch andere Nervenzellen miteinander verschaltet waren, wurden zeitlich gepaart elektrisch gereizt. Die unterschiedlichen
Zeitverzogerungen der parallelen Leitungen bewirkten in Kombination mit
der Struktur des Lernfensters, da ein
Teil der beteiligten Synapsen verstarkt
und ein anderer Teil abgeschwacht wurde: die Hebbsche Lernregel fuhrt in
komplexeren Netzwerken zur Ausbildung charakteristischer raumzeitlicher
Strukturen.
Mittlerweile existiert eine Reihe
von theoretischen Arbeiten, die das
zeitabhangige Hebbsche Lernen in
Netzwerken aus spikenden Neuronen
untersuchen (z. B. [12, 7, 8, 19]).
Eine typische Lernregel sieht folgendermaen aus: Betrachtet man eine
Synapse, mit der Neuron j auf Neuron
i einwirkt, dann wird aufgrund eines
Abbildung 10: Hebbsches Lernfenster
fur Mittelhirnneuronen einer Kaulquappe, die Eingaben von Retinaganglienzellen bekommen. Auf der Abszisse ist die Zeitdierenz zwischen den
Aktivitaten der vor- und der nachgeschalteten Zelle aufgetragen, die Or
dinate zeigt die Anderung
des in
die nachgeschaltete Zelle einieenden
Stroms (Excitatory PostSynaptic Current, EPSC) aufgrund von 100 elektrischen Stimulationen. In den Gebieten I
und II wirkt das vorgeschaltete Neuron
kausal auf das nachgeschaltete Neuron
ein, und die Synapse wird verstarkt; in
Gebiet III ist die Wechselwirkung akausal (zufallig), und die Synapse wird abgeschwacht. Abbildung aus [23].
Spikes zur Zeit tj im vorgeschalteten
Neuron und eines Spikes zur Zeit ti im
nachgeschalteten Neuron die Synapse
wie folgt verandert:
wijneu = wijalt + W (tj ; ti ) ; (12)
wobei W beispielsweise das in Abbildung 10 dargestellte Lernfenster ist.
Lernen erfolgt in einem Netzwerk aus
spikenden Neuronen dann zwischen allen Spikepaaren von miteinander ver-
schalteten Neuronen.
Gerstner et al. [12] verwenden eine
zeitsensitive Lernregel, um eine Serie
von Zeitverzogerungsstrecken (realisiert
durch unterschiedliche Signallaufzeiten
in den Axonen verschiedener Neuronen)
selbstorganisiert entstehen zu lassen.
Das verwendete Netzwerk steht modellhaft fur eine Struktur im Mittelhirn der
Eule, wo fein abgestimmte Zeitverzogerungsstrecken zur auditorischen Lokalisation von Beute herangezogen werden [5]. Eurich et al. [7, 8] beschaftigen sich ebenfalls mit der Adaptivitat
von Zeitverzogerungen und leiten Bedingungen an das Hebbsche Lernfenster
her, die dazu fuhren, da raumzeitliche Spikemuster stabil in einem neuronalen Netz gespeichert werden konnen;
solche stabilen Spikesequenzen konnen
gezielt nachgeschaltete Neuronen anregen, und die auf diese Weise etablierten Schaltkreise haben moglicherweise
eine Funktion im Zusammenhang mit
dem Gedachtnis. Song et al. [19] schlielich zeigen unter anderem, da Instabilitaten wie die oben im Zusammenhang
mit der alten Lernregel (11) beschriebenen bei der neuen, zeitsensitiven Lernregel (12) nicht auftreten.
Synaptische Plastizitat und Lernen. Obwohl Neurowissenschaftler
seit der Entdeckung von LTP und LTD
daran geglaubt haben, da synaptische
Plastizitat ein neuronales Korrelat von
Lernvorgangen darstellt, ist dies erst
vor wenigen Monaten (im Oktober
2000) demonstriert worden. RioultPedotti et al. [18] trainierten Ratten
auf eine motorische Aufgabe, dem Herausangeln von kleinen Futterkugeln aus
einer Box mit Hilfe einer Vorderpfote. [6] C. W. Eurich, Neuronale Netze,
Anschlieend wurde nachgewiesen,
in: Lexikon der Physik, Spektrum,
da bei den trainierten Tieren | im
Heidelberg (2000), 81{86.
Vergleich zu einer Kontrollgruppe |
LTP im motorischen Cortex, der fur die [7] C. W. Eurich, J. D. Cowan und
J. G. Milton, Hebbian delay adSteuerung von Bewegungen zustandig
aptation in a network of integrateist, stattgefunden hatte. Mit diesem
and-re neurons, in: W. Gerstner,
Nachweis haben sich die Hebbschen
A. Germond, M. Hasler und J.Ideen uber Lernen und Plastizitat im
D. Nicoud (eds), Articial Neural
Nervensystem mehr als 50 Jahre nach
Networks { ICANN '97, Springerihrer Formulierung ganzlich bestatigt.
Verlag, Berlin (1997), 157{162.
[8] C. W. Eurich, K. Pawelzik,
Literatur
U. Ernst, J. D. Cowan und J. G.
Milton, Dynamics of self-organized
[1] G.-q. Bi und M.-m. Poo, Synapdelay adaptation, Phys. Rev. Lett.
tic modications in cultured hip82 (1999) 1594{1597.
pocampal neurons: dependence on
spike timing, synaptic strength, [9] C. W. Eurich und S. D. Wilke,
Multi-dimensional encoding straand postsynaptic cell type, J. Neutegy of spiking neurons, Neural
rosci. 18 (1998) 10464{10472.
Comp. 12 (2000) 1519{1529.
[2] G.-q. Bi und M.-m. Poo, Distributed synaptic modication in neural [10] C. W. Eurich, S. D. Wilke und
H. Schwegler, Neural representanetworks induced by patterned stition of multi-dimensional stimuli,
mulation, Nature 401 (1999) 792{
in: S. A. Solla, T. K. Leen und
796.
K.-R. Muller (eds), Advances in
Neural Information Processing Sy[3] T. H. Brown, P. F. Chapmann,
stems 12, MIT Press, Cambridge
E. W. Kairiss und C. L. Keenan,
MA (2000), 115{121.
Long-term synaptic potentiation,
Science 242 (1988) 724{728.
[11] D. Felleman und D. C. van Essen,
Distributed hierarchical processing
[4] T. H. Brown, E. W. Kairiss und
in the primate cerebral cortex, CeC. L. Keenan, Hebbian synapses:
rebral Cortex 1 (1991) 1{47.
biophysical mechanisms and algorithms, Annu. Rev. Neurosci. 13 [12] W. Gerstner, R. Kempter, J. L.
(1990) 475{511.
van Hemmen und H. Wagner, A
neuronal learning rule for sub[5] C. E. Carr und M. Konishi, A cirmillisecond temporal coding, Nacuit for detection of interaural time
ture 383 (1996) 76{78.
dierences in the brain stem of the
barn owl, J. Neurosci. 10 (1990) [13] D. O. Hebb, The Organization of
3227{3246.
Behavior, Wiley, New York (1949).
framework with application to hippocampal place cells, J. Neurophysiol. 79 (1998) 1017{1044.
[22] K. Zhang und T. J. Sejnowski,
Neuronal tuning: to sharpen or
[15] H. Markram, J. Lubke, M. Frotbroaden?, Neural Comp. 11 (1999)
scher und B. Sakmann, Regulation
75{84.
of synaptic ecacy by coincidence
of postsynaptic APs and EPSPs,
[23] L. I. Zhang, H. W. Tao, C. E.
Science 275 (1997) 213{215.
Holt, W. A. Harris und M.-m. Poo,
A critical window for cooperation
[16] M. A. Paradiso, A theory for the
and competition among developing
use of visual orientation informaretinotectal synapses, Nature 395
tion which exploits the columnar
(1998) 37{44.
structure of striate cortex, Biol.
Cybern. 58 (1988) 35{49.
[14] S. M. Kay, Fundamentals of Statistical Signal Processing. Volume I:
Estimation Theory, Prentice Hall,
Upper Saddle River, NJ (1993).
[17] F. Rieke, D. Warland, R. de Ruyter van Steveninck und W. Bialek, Spikes - Exploring the Neural
Code, MIT Press, Cambridge, MA
(1997).
[18] M.-S. Rioult-Pedotti, D. Friedman
und J. P. Donoghue, Learninginduced LTP in neocortex, Science
290 (2000) 533{536.
[19] S. Song, K. D. Miller und L. F.
Abbott, Competitive Hebbian
learning through spike-timingdependent synaptic plasticity,
Nature Neurosci. 3 (2000) 919{
926.
[20] G. J. Stuart und B. Sakmann, Active propagation of somatic action potentials into neocortical pyramidal cell dendrites, Nature 367
(1994) 69{72.
[21] K. Zhang, I. Ginzburg, B. L. McNaughton und T. J. Sejnowski, Interpreting neuronal population activity by reconstruction: a unied