Lösungen zum Übungsblatt "Abbildungen"
Werbung
Institut für Stochastik,
Fernstudienzentrum
Vorkurs Mathematik für die Fachrichtung
Wirtschaftswissenschaften im Herbst 2014
Übungsaufgaben zum Thema Abbildungen
Aufgabe 1
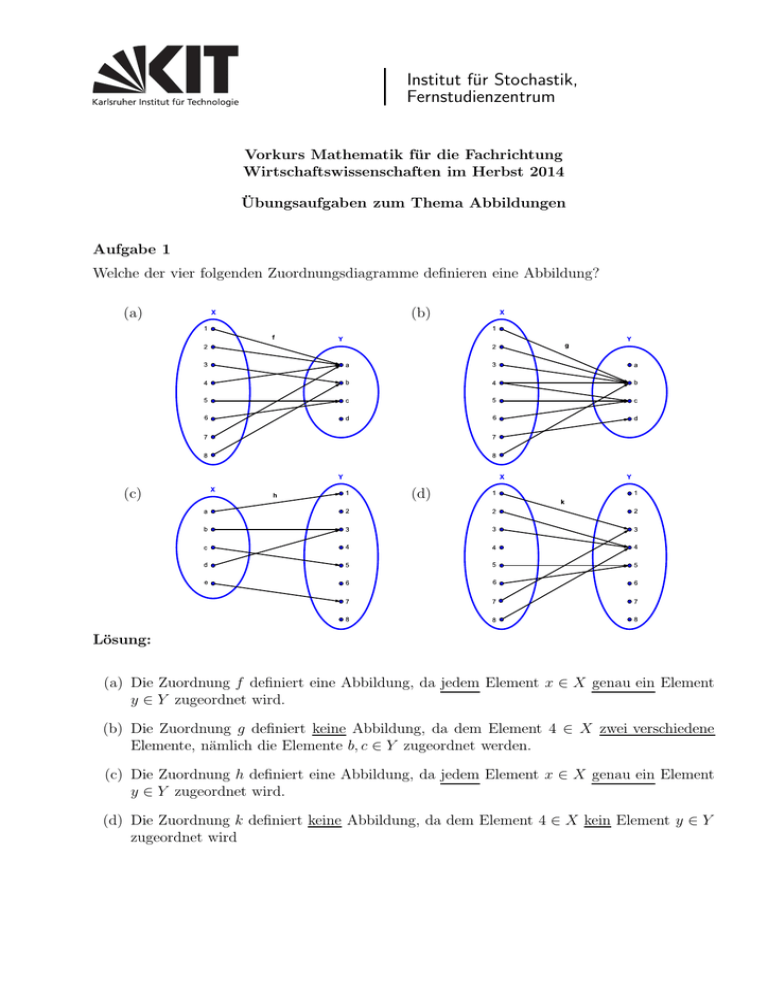
Welche der vier folgenden Zuordnungsdiagramme definieren eine Abbildung?
(a)
(b)
(c)
(d)
Lösung:
(a) Die Zuordnung f definiert eine Abbildung, da jedem Element x ∈ X genau ein Element
y ∈ Y zugeordnet wird.
(b) Die Zuordnung g definiert keine Abbildung, da dem Element 4 ∈ X zwei verschiedene
Elemente, nämlich die Elemente b, c ∈ Y zugeordnet werden.
(c) Die Zuordnung h definiert eine Abbildung, da jedem Element x ∈ X genau ein Element
y ∈ Y zugeordnet wird.
(d) Die Zuordnung k definiert keine Abbildung, da dem Element 4 ∈ X kein Element y ∈ Y
zugeordnet wird
Aufgabe 2
Es sei X = Y = {1, 2, 3, 4, 5, 6, 7, 8}. Die Abbildung f : X → Y, x 7→ y = f (x), sei durch das
folgende Zuordnungsdiagramm definiert.
1. Geben Sie die Menge Bild(f ) ⊂ Y an.
2. Es sei A = {1, 2, 3, 5} ⊂ X. Geben Sie die Menge f (A) ⊂ Y an.
3. Es sei B = {1, 2, 3, 7} ⊂ Y . Geben Sie die Menge f −1 (B) ⊂ X an.
4. Es sei C = {1, 2, 3, 4} ⊂ X. Geben Sie die Menge f −1 (f (C)) ⊂ X an.
5. Es sei D = {1, 2, 3, 8} ⊂ Y . Geben Sie die Menge f (f −1 (D)) ⊂ Y an.
Lösung:
1. Bild(f ) = f (X) = {1, 3, 4, 5, 7}.
2. f (A) = f ({1, 2, 3, 5}) = {3, 4, 5, 7}.
3. f −1 (B) = f −1 ({1, 2, 3, 7}) = {1, 2, 4, 7}.
4. f −1 (f (C)) = f −1 (f ({1, 2, 3, 4})) = f −1 ({3, 4, 7}) = {1, 2, 3, 4, 8}.
5. f (f −1 (D)) = f (f −1 ({1, 2, 3, 8})) = f ({1, 4, 7}) = {1, 3}.
2
Aufgabe 3
Vorgegeben seien vier Abbildungen f1 , f2 , f3 , f4 , definiert jeweils durch ein Zuordnungsdiagramm. Welche dieser Abbildungen ist injektiv bzw. surjektiv bzw. bijektiv?
(a)
(b)
(c)
(d)
Lösung:
(a) Die Abbildung f1 ist injektiv, weil in der Zuordnung f1 auf jedes Element y ∈ Y höchstens
ein Pfeil verweist. Die Abbildung f1 ist auch surjektiv, da auf jedes Element y ∈ Y mindestens ein Pfeil verweist. Also ist die Abbildung f1 injektiv und surjektiv, also bijektiv.
Man beachte, dass bei der Zuordnung f1 auf jedes Element y ∈ Y genau ein Pfeil verweist.
(b) Die Abbildung f2 ist nicht injektiv, da z.B. auf das Element a ∈ Y drei verschiedene
Pfeile verweisen. Die Abbildung f2 ist surjektiv, da auf jedes Element y ∈ Y mindestens
ein Pfeil verweist. Da die Abbildung f2 nicht injektiv ist, ist sie auch nicht bijektiv.
(c) Die Abbildung f3 ist injektiv, weil in der Zuordnung f3 auf jedes Element y ∈ Y höchstens
ein Pfeil verweist. Die Abbildung f3 ist nicht surjektiv, also insbesondere auch nicht
bijektiv, da z.B. auf das Element 1 ∈ Y kein Pfeil verweist.
(d) Die Abbildung f4 ist nicht injektiv, da z.B. auf das Element b ∈ Y mehrere verschiedene
Pfeile verweisen. Sie ist auch nicht surjektiv, da z.B. auf das Element a ∈ Y kein Pfeil
verweist. Insbesondere ist die Abbildung f4 auch nicht bijektiv.
3
Aufgabe 4
Vorgegeben seien die beiden Abbildungen f : X → Y, x 7→ f (x), und g : Y → X, y 7→ g(y),
jeweils definiert durch die beiden folgenden Zuordnungsdiagramme.
1. Geben Sie das Zuordnungsdiagramm der Abbildung
g ◦ f : X → X, x 7→ (g ◦ f )(x) = g(f (x))
an.
2. Geben Sie das Zuordnungsdiagramm der Abbildung
f ◦ g : Y → Y, y 7→ (f ◦ g)(y) = f (g(y))
an.
3. Ist die Abbildung g ◦ f injektiv bzw. surjektiv bzw. bijektiv?
4. Ist die Abbildung f ◦ g injektiv bzw. surjektiv bzw. bijektiv?
Lösung:
1. Die Hintereinanderausführung ”erst f ” und ”dann g”
ergibt das Zuordnungsdiagramm der Abbildung g ◦ f : X → X, x 7→ (g ◦ f )(x) = g(f (x)).
4
2. Die Hintereinanderausführung ”erst g” und ”dann f ”
ergibt das Zuordnungsdiagramm der Abbildung f ◦ g : Y → Y, y 7→ (f ◦ g)(y) = f (g(y)).
3. Die Abbildung g ◦ f ist nicht injektiv wegen
(g ◦ f )(2) = g(f (2)) = g(b) = 2 = g(b) = g(f (3)) = (g ◦ f )(3).
Die Abbildung g ◦ f ist auch nicht surjektiv wegen
1∈
/ Bild(g ◦ f ) = {2, 4, 5, 6}.
Insbesondere ist die Abbildung g ◦ f nicht bijektiv.
4. Die Abbildung f ◦ g ist nicht injektiv wegen
(f ◦ g)(a) = f (g(a)) = f (1) = e = f (6) = f (g(d)) = (f ◦ g)(d).
Die Abbildung f ◦ g ist auch nicht surjektiv wegen
a∈
/ Bild(f ◦ g) = {b, c, d, e}.
Insbesondere ist die Abbildung f ◦ g nicht bijektiv.
5
Aufgabe 5
Vorgegeben seien die Intervalle X = [0, 2] und Y = [0, 4]. Entscheiden Sie aufgrund der Schaubilder der Graphen, welche der folgenden sechs Abbildungen
fi : X → Y, x 7→ y = fi (x), i = 1, 2, 3, 4, 5, 6,
injektiv, surjektiv und bijektiv sind.
(a) f1 (x) = x + 2,
(d) f4 (x) =
1
2
· x2 ,
(b) f2 (x) = 4 − 2 · x,
(c) f3 (x) = |x − 1|,
(e) f5 (x) = 4 · (x − 1)2 ,
(f) f6 (x) = |x2 − 1|.
Lösung:
(a)
(b)
(c)
(d)
(e)
(f)
(a) Die Abbildung
f1 : [0, 2] → [0, 4], x 7→ y = f1 (x) = x + 2,
ist injektiv, aber nicht surjektiv, also insbesondere auch nicht bijektiv.
6
(b) Die Abbildung
f2 : [0, 2] → [0, 4], x 7→ y = f2 (x) = 4 − 2 · x,
ist injektiv und surjektiv, folglich auch bijektiv.
(c) Die Abbildung
f3 : [0, 2] → [0, 4], x 7→ y = f3 (x) = |x − 1|,
ist nicht injektiv und nicht surjektiv, insbesondere auch nicht bijektiv.
(d) Die Abbildung
f4 : [0, 2] → [0, 4], x 7→ y = f4 (x) =
1
2
· x2 ,
ist injektiv, aber nicht surjektiv, also insbesondere auch nicht bijektiv.
(e) Die Abbildung
f5 : [0, 2] → [0, 4], x 7→ y = f5 (x) = 4 · (x − 1)2 ,
ist nicht injektiv, aber surjektiv, also insbesondere auch nicht bijektiv.
(f) Die Abbildung
f6 : [0, 2] → [0, 4], x 7→ y = f6 (x) = |x2 − 1|,
ist nicht injektiv und nicht surjektiv, insbesondere auch nicht bijektiv.
Aufgabe 6
Vorgegeben seien die folgenden beiden Abbildungen
f1 : R2 → R2 , (x, y) 7→ f1 (x, y) = (x − y, x + y),
f2 : R2 → R2 , (x, y) 7→ f2 (x, y) = (2 · x + y, 4 · x + 2 · y).
Untersuchen Sie diese beiden Abbildungen auf Injektivität, Surjektivität und Bijektivität.
Lösung:
1. f1 : R2 → R2 , (x, y) 7→ f1 (x, y) = (x − y, x + y).
Zunächst wird die Frage der Surjektivität beantwortet. Es sei (a, b) ∈ R2 ein beliebiger
Punkt im R2 . Das lineare Gleichungssystem
x
x
− y
+ y
=
=
a,
b,
ist eindeutig lösbar. Die Lösung erhält man wie folgt. Die Addition der beiden Gleichungen
ergibt
2 · x = a + b, also x =
7
a+b
,
2
und Einsetzen in einer der beiden Gleichungen (z.B. in die zweite) ergibt
a+b
a+b
b−a
+ y = b, also y = b −
=
.
2
2
2
Also lautet die eindeutig bestimmte Lösung des linearen Gleichungssystems
a+b b−a
,
,
(x0 , y0 ) =
2
2
und es folgt
f1 (x0 , y0 ) = f1
a+b b−a
,
2
2
= (a, b).
Folglich ist die Abbildung f1 surjektiv, denn jeder Punkt (a, b) aus dem Wertebereich ist
ein Bildpunkt eines Punktes (x0 , y0 ) aus dem Definitionsbereich. Bis hier ist nur ausgenutzt worden, dass das lineare Gleichungssystem stets Lösungen hat. Es ist aber schon
festgestellt worden, dass das lineare Gleichungssystem sogar stets eindeutig lösbar ist, d.h.
zu jedem Punkt (a, b) ∈ R2 gibt es genau einen Punkt (x0 , y0 ) aus dem Definitionsbereich
mit f (x0 , y0 ) = (a, b). Dies bedeutet, dass die Abbildung f1 auch injektiv ist. Insgesamt
ergibt sich, dass die Abbildung f1 bijektiv ist.
2. f2 : R2 → R2 , (x, y) 7→ f2 (x, y) = (2 · x + y, 4 · x + 2 · y).
Auch hier wird zunächst wieder für (a, b) ∈ R2 das lineare Gleichungssystem
2·x +
4·x +
y
2·y
=
=
a,
b,
untersucht. Subtrahiert man von der zweiten Gleichung zweimal die erste, so erhält man
0 = b − 2 · a.
Dies bedeutet, das dieses lineare Gleichungssytem nur lösbar ist, falls
b=2·a
gilt. So ist z.B. das lineare Gleichungssytem unlösbar für (a, b) = (1, 0). Dies bedeutet
(1, 0) ∈
/ Bild(f2 ) = f (R2 ).
Folglich ist die Abbildung f2 nicht surjektiv. Die Abbildung f2 ist auch nicht injektiv,
denn das lineare Gleichungssystem
2·x
4·x
+
y
+ 2·y
= 0,
= 0,
besitzt unendlich viele Lösungen. Die Lösungsmenge des letzten linearen Gleichungssystems lautet
L = {(x, y) ∈ R2 : y = −2 · x}.
8
Geometrisch bilden die Punkte aus L eine Gerade durch den Nullpunkt mit der Steigung
(−2). Es gilt z.B.
f2 (0, 0) = 0 = f2 (1, −2).
Insbesondere ist die Abbildung f2 auch nicht bijektiv.
Aufgabe 7
Die Anzahl der Einheiten eines Gutes, die Verbraucher in einer bestimmten Periode nachfragen
(d.h. bereit sind zu kaufen), hängt vom Preis dieses Gutes ab. Im Allgemeinen wird die Nachfrage zurückgehen, wenn der Preis steigt. Die Anzahl der Einheiten, die die Hersteller innerhalb
einer gewissen Zeitperiode bereit sind, dem Markt anzubieten, hängt auch vom Preis ab, den
sie erzielen können. Im Allgemeinen wird das Angebot steigen, wenn der Preis steigt. Typische
Nachfrage- und Angebotsfunktionen (als Funktionen des Preises P ) sehen wie im folgenden
Schaubild aus.
Der Punkt E, in dem die Nachfrage gleich dem Angebot ist, stellt das Gleichgewicht dar.
Der Preis P ∗ , bei dem dies eintritt, ist der Gleichgewichtspreis und die zugehörige Menge
Q∗ ist die Gleichgewichtsmenge. Der Gleichgewichtspreis ist also der Preis, bei dem die
Verbraucher die gleiche Menge dieses Gutes kaufen wollen, wie die Hersteller bei diesem Preis
verkaufen wollen.
Beispiel
Betrachtet wird das lineare Nachfrage- und Angebotsmodell
D = 100 − P ,
S = 10 + 2 · P .
Hier ist die Nachfrage gleich dem Angebot, falls
100 − P = 10 + 2 · P
gilt, also für
3 · P = 90,
9
also lautet der Gleichgewichtspreis P ∗ = 30 mit der zugehörigen Gleichgewichtsmenge Q∗ = 70.
Aufgabe:
Betrachten Sie die folgenden allgemeinen linearen Nachfrage- und Angebotsmodelle:
D = a − b · P,
S = α + β · P.
Dabei sind a und b positive Parameter der Nachfragefunktion D, während α, β positive Parameter der Angebotsfunktion S sind. Bestimmen Sie den Gleichgewichtspreis P ∗ und die zugehörige
Gleichgewichtsmenge Q∗ in diesem Modell.
Lösung:
Beim Gleichgewichtspreis P ∗ ist die Nachfrage gleich dem Angebot, so dass D = S an der Stelle
P = P ∗ gelten muss. Daher ist
a − b · P ∗ = α + β · P ∗.
Addiert man auf beiden Seiten b · P ∗ − α, so erhält man
a − b · P ∗ + b · P ∗ − α = α + β · P ∗ + b · P ∗ − α,
also
a − α = P ∗ · (β + b).
Es folgt
P∗ =
a−α
.
β+b
Die zugehörige Gleichgewichtsmenge ergibt sich dann zu
Q∗ = a − b · P ∗ = a − b ·
10
a·β+α·b
a−α
=
.
β+b
β+b