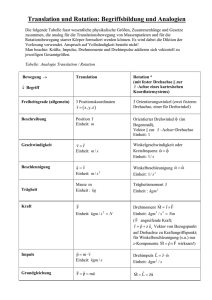
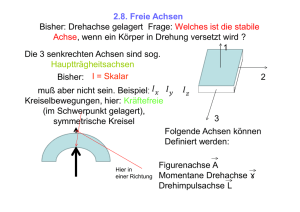
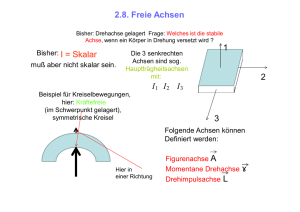
DAS DYNAMISCHE GRUNDGESETZ

Skriptum zum Fach Mechanik 3.Jahrgang HTL-Eisenstadt
DAS DYNAMISCHE GRUNDGESETZ
Dipl.Ing.Dr.Günter Hackmüller
©2005 Dipl.Ing.Dr.Günter Hackmüller
Alle Rechte vorbehalten
e-mail: [email protected]
DIE KINETIK
Die Kinetik untersucht den Zusammenhang zwischen den Kräften und Momenten, die auf
einen Körper wirken, und den Bewegungen, die unter dem Einfluss dieser Kräfte und
Momente ablaufen.
1.Die Kinetik der Punktmasse
Eine Punktmasse ist eine im Massenmittelpunkt konzentriert gedachte Masse eines Körpers.
Wirkliche Körper besitzen immer eine räumliche Ausdehnung. Man darf sie sich durch eine
Punktmasse ersetzt denken, wenn
•
der Körper eine Translationsbewegung ausführt (alle Punkte haben dieselbe
Geschwindigkeit wie der Massenmittelpunkt);
•
von der Eigendrehung des Körpers abgesehen werden kann.
Im Rahmen dieses Abschnittes ist immer eine Punktmasse gemeint, wenn von einem Körper
gesprochen wird.
a.Die Newtonschen Axiome
1.Newtonsches Axiom: In ausgezeichneten Bezugssystemen, den Inertialsystemen,
verharrt eine Punktmasse im Zustand der Ruhe oder der gleichförmigen Bewegung,
wenn sie nicht durch einwirkende Kräfte gezwungen wird, diesen Zustand zu ändern.
Jedes gegenüber einem Inertialsystem gleichförmig bewegte Bezugssystem ist ebenfalls ein
Inertialsystem. Für technische Berechnungen werden meist die mit der Erde fest verbundenen
Bezugsysteme als Inertialsysteme betrachtet.
2.Newtonsches Axiom: Die an einer Punktmasse angreifende Kraft und die durch sie
hervorgerufenen Beschleunigung sind gleichgerichtet und einander proportional:
v
v
F = m⋅a
.
In Komponenten geschrieben bedeutet dies
••
Fx = m ⋅ x = m ⋅ a x
••
Fy = m ⋅ y = m ⋅ a y
.
Das zweite Newtonsche Axiom schreibt jedem Körper eine träge Masse m zu.
Ein Kilogramm ist die träge Masse eines in Paris aufbewahrten Normalkörpers, das
Urkilogramm: m = 1kg .
Die Größe jeder anderen Masse lässt sich wenigstens im Prinzip durch den Vergleich der
Beschleunigungen ermitteln, die ein und dieselbe Kraft einmal dem Urkilogramm und das
andere Mal der gegebenen Masse erteilt.
Die Kraft ist im Internationalen Maßsystem eine abgeleitete Größe. Ihre Einheit ist das
Newton F = 1N . Ein Newton ist die Kraft, die der Masse m = 1kg eine Beschleunigung
m
kgm
a = 1 2 erteilt: 1 N = 1 2
s
s
3.Newtonsches Axiom: Wird von einer Punktmasse auf eine andere eine Kraft (Aktio)
ausgeübt, so bedingt dies, dass der zweite Körper auf den ersten ebenfalls eine Kraft
ausübt (Reaktion), die mit der ersten Kraft in Betrag und Wirkungslinie übereinstimmt,
jedoch entgegengesetzt gerichtet ist: Aktion=Reaktion.
Kräfte treten also stets paarweise auf. Aktionskraft und Reaktionskraft wirken aber an
verschiedenen Körpern.
b.Zwangskräfte: Bei vielen Problemen treten Zwangsbedingungen auf, die dem Bewegungsablauf geometrische Beschränkungen auferlegen. Dadurch verringert sich die die Zahl
der Freiheitsgrade, dh. die Zahl der unabhängigen Koordinaten, die für die Beschreibung der
Bewegung des Systems benötigt werden.
Jede solche Zwangsbedingung macht sich in Gestalt einer zugehörigen Zwangskraft bemerkbar, die auf das System wirkt. Das betrachtete System folgt der Zwangsbedingung nur,
weil es durch diese Zwangskraft dazu genötigt wird. Die Zwangskräfte werden auch als
Reaktions- oder Führungskräfte bezeichnet.
Während die Wirkung der Zwangskräfte bekannt ist, kennt man die Zwangskräfte selbst i.a.
nicht vollständig. Die Newtonschen Axiome allein reichen nicht aus, um Aufgaben mit
Zwangsbedingungen zu lösen. Man benötigt vielmehr Informationen betreffend die Natur der
Zwangskräfte.
Berührungskräfte: An der Kontaktstelle zweier Körper wirkt eine Normalkraft senkrecht auf
die Berührebene und eine Tangentialkraft oder Reibungskraft in der Berührebene.
•
•
Reibungskräfte treten i.a. nur auf, wenn die beiden Kontaktflächen aneinander abgleiten
können.
Reibungskräfte versuchen das Abgleiten der beiden Kontaktflächen zu verhindern.
c.Wesentliche Kräfte
Gewichtskraft: Überlässt man einen Körper in der
r Nähe der Erdoberfläche sich selbst, so
bewegt er sich mit konstanter Erdbeschleunigung g in Richtung auf den Erdmittelpunkt. Auf
den Körper wirkt daher eine Gewichts- oder Schwerkraft:
FG = m ⋅ g
mit
g = 9.81
m
s2
.
Luftkräfte: Bei der Relativbewegung eines starren Körpers in flüssigen und gasförmigen
Medien treten Kräfte auf. Man unterscheidet zwischen der Auftriebskraft FA senkrecht zur
Bewegungsrichtung und der Widerstandskraft FW entgegen der Bewegungsrichtung. Beide
hängen von der Dichte ρ des umgebenden Mediums, der Relativgeschwindigkeit V , einer
gewählten Bezugsfläche A des Körpers und einem Auftriebs- bzw. Widerstandsbeiwert ab.
FA = c A ⋅
ρ
2
⋅ V2 ⋅ A
FW = c W ⋅
ρ
2
⋅ V2 ⋅ A .
Bei kleinen Geschwindigkeiten (kleine Reynoldszahl) – man spricht von schleichender
Strömung – ist der Widerstandsbeiwert proportional zum Kehrwert der Geschwindigkeit
c W ≈ konst ⋅ V −1 . Die Widerstandskraft ist dann proportional zur Geschwindigkeit
FW ≈ konst. ⋅ V . Dieses Reibungsgesetz spielt bei gedämpften Schwingungen eine Rolle.
Bei großen Geschwindigkeiten (große Reynoldszahl) kann der Widerstandsbeiwert oft als
konstant angenommen werden.
Federkraft: Um eine Feder zu dehnen ist eine Kraft erforderlich. Bei einer linearen Feder
sind Längenänderung und erforderliche Kraft proportional zueinander. Die
Proportionalitätskonstante c ist die Federkonstante:
FF = c ⋅ ∆L
Dämpferkraft: Um einen Dämpfer mit der Geschwindigkeit V zu öffnen ist eine Kraft
erforderlich. Diese wird als proportional zur Öffnungsgeschwindigkeit V mit der
Dämpferkonstanten k angesetzt:
FD = k ⋅ V
Reibungskraft: An einer Stelle der Berührung zweier Körper wirkt eine Kraft normal auf die
Berührebene - Normalkraft - und eine Kraft, die in der Berührebene liegt – Reibungskraft.
Die Reibungskraft versucht eine Relativbewegung zwischen den beiden Körpern zu verhindern.
Haften: Von Haften spricht man, wenn diese Reibungskraft FR zwischen zwei berührenden
Körpern ausreicht, um eine Relativbewegung der beiden Körper zu verhindern. Die Größe
dieser Reibungskraft ist nach oben durch die Haftreibungskraft begrenzt. Diese
Haftreibungskraft F R 0 ist proportional zur Normalkraft F an der Berührungsstelle:
N
F K ≤ F R 0 = µ 0 ⋅ FN
.
Die Proportionalitätsgrenze µ 0 ist die Haftreibzahl.
Gleiten: Übersteigt die erforderliche Kontaktkraft die Haftreibungkraft, so setzt Gleiten ein.
An der Berührungsstelle wirkt dann die Gleitreibungskraft:
F R = µ ⋅ FN
,
die wieder proportional zur Normalkaft an der Berührungsstelle ist. Die Proportionalitätskonstante µ heißt nun aber Gleitreibungszahl.
Rollwiderstand: Auch beim Abrollen eines Körpers auf einer Unterlage entsteht ein
Bewegungswiderstand, der proportional zur Normalkraft an der Berührungsstelle ist:
Froll = µ roll ⋅ FN
.
2.Die Kinetik des starren Körpers
Jede ebene Bewegung eines Körpers setzt sich aus einer Translation in der Ebene der
Bewegung und einer Rotation um eine Achse senkrecht zur Ebene der Bewegung
zusammen. Der Körper hat daher zwei Translations- und einen
Rotationsfreiheitsgrad. Für jeden dieser Freiheitsgrade ist eine Bewegungsgleichung
erforderlich. Insgesamt wird jede ebene Bewegung eines starren Körpers durch drei
Bewegungsgleichungen beschrieben.
Der Schwerpunktsatz:
Der Schwerpunkt eines starren Körpers bewegt sich so, als ob die gesamte Masse
in ihm vereinigt wäre und die Resultierende aller äußeren Kräfte an ihm angreifen
würde:
v
v
F = m⋅a
.
In Komponenten geschrieben bedeutet dies
••
Fx = m ⋅ x = m ⋅ a x
••
Fy = m ⋅ y = m ⋅ a y
.
Der Momentensatz:
Ein Drehmoment, das auf einen Körper wirkt, verursacht eine
Winkelbeschleunigung α . Zwischen dem äußeren Moment M A um eine zur Ebene
der Bewegung senkrechte Achse durch einen der unten angegebenen ausgewählten
Drehpunkte A und der Winkelbeschleunigung α besteht der Zusammenhang
•
MA = J A ⋅ω = J A ⋅α
.
M A ............ Moment der äußeren Kräfte um A
J A ............. Massenträgheitsmoment bezüglich A
ω .............. Winkelgeschwindigkeit der Drehbewegung
α ............... Winkelbeschleunigung
Ausgewählte Drehpunkte A sind:
•
•
festgehaltene Achse durch A
Körperschwerpunkt
Der Drehpunkt A darf nicht beliebig gewählt werden. Der Satz gilt in dieser Form nur,
wenn die Drehachse durch den Punkt A festgehalten wird oder wenn als Bezugspunkt
für die Bildung des Momentes der Körperschwerpunkt S gewählt wird. Nur für den
Fall, dass der Abstand des Momentanpols vom Körperschwerpunkt bei der Bewegung
konstant bleibt, darf auch der Momentanpol als Drehpunkt A gewählt werden.
Die Größe der Winkelbeschleunigung, die ein gegebenes Moment verursacht, hängt
vom Massenträgheitsmoment des Körpers bezüglich des Drehpunktes A ab:
J A = ∫ r 2 ⋅ dm
.
J A ............. Massenträgheitsmoment bezüglich einer Drehachse durch A
r ............... Abstand des Masseelementes dm vom Drehpunkt A
Ist das Massenträgheitsmoment J S bezüglich einer Drehachse durch den Schwerpunktes
S bekannt, kann das Massenträgheitsmoment J A um eine parallele Drehachse durch
eine beliebigen anderen Drehpunkt A mit Hilfe des Satzes von Steiner berechnet
werden:
J A = JS + m ⋅ a2
.
J A ............. Massenträgheitsmoment bezüglich einer Drehachse durch A
J S .............. Massenträgheitsmoment bezüglich einer parallelen Achse durch den
Körperschwerpunkt
m............... Masse des Körpers
a ............... Abstand der beiden parallelen Drehachsen
2.1.Begründung des Schwerpunktsatzes und des Momentensatzes
Betrachten wir die ebene Bewegung eines starren Körpers unter dem Einfluss äußerer
Kräfte. Als Bezugspunkt A wählen wir einen beliebigen körperfesten Punkt. Für die
kartesischen Koordinaten eines beliebigen Massenelementes gilt dann (siehe Abb.)
x = x A + ξ = x A + r ⋅ cos ϕ
y = y A + η = y A + r ⋅ sin ϕ
.
Der Körper ist starr. Der Abstand r des
betrachteten
Masseelementes
vom
gewählten Bezugspunkt A ist daher
konstant. Der Winkel ϕ wird im
mathematisch positiven Sinn von der xAchse weg gezählt.
dMT
dMT
Die Geschwindigkeitskomponenten des
Masseelementes dm erhält man durch
einmalige Ableitung der Koordinaten
nach der Zeit:
•
•
•
•
•
•
x = x A − ω ⋅ r ⋅ sin ϕ = x A − ω ⋅ η
.
y = y A + ω ⋅ r ⋅ cos ϕ = x A + ω ⋅ ξ
•
Für die Winkelgeschwindigkeit gilt ω = ϕ . Eine nochmalige Ableitung nach der Zeit
liefert die Beschleunigungskomponenten:
••
••
•
••
•
••
••
•
••
•
x = x A − ω 2 ⋅ r ⋅ cos ϕ − ω ⋅ r ⋅ sin ϕ = x A − ω 2 ⋅ ξ − ω ⋅ η
y = y A − ω 2 ⋅ r ⋅ sin ϕ + ω ⋅ r ⋅ cos ϕ = y A − ω 2 ⋅ η + ω ⋅ ξ
.
Diesen Körper denken wir uns nun in Elemente der Masse dm zerlegt. An diesen
Massenelementen wirkt i.a. neben den Kräfte dFx, dFy noch ein inneres Moment dMT.
Für elastische Materialien - und der starre Körper kann als Grenzfall eines elastischen
Materials mit unendlich großem E-Modul betrachtet werden - gilt der Satz von den
zugeordneten Schubspannungen. Dies ist gleichbedeutend damit, dass das innere
Moment dann identisch null ist: dMT = 0. Im folgenden wird dieser Term daher nicht
mehr berücksichtigt.
Gemäß dem zweiten Newtonschen Axiom bewirken die beiden
Beschleunigungen des Teilchens in die beiden Koordinatenrichtungen.:
••
••
dFx = dm ⋅ x und dFy = dm ⋅ y
Kräfte
.
Für das Moment dieser Kraft bezüglich des gewählten Bezugspunktes A gilt
dM A = dFy ⋅ ξ − dFx ⋅η
.
Erfahrungsgemäß ändert kein Köper ohne äußere Kraft oder äußeres Moment seinen
Bewegungszustand. Die erforderliche äußere Kraft und das erforderliche äußere
Moment, die notwendig sind, um den ganzen Körper zu beschleunigen, erhält man
daher durch Integration über alle Massenelemente. Einsetzen der abgeleiteten
Ausdrücke für die Komponente der Beschleunigung liefert
••
•
••
•
Fx = ∫ dFx = x A ∫ dm − ω 2 ∫ ξ ⋅ dm − ω ∫ η ⋅ dm
Fy = ∫ dFy = y A ∫ dm − ω 2 ∫ η ⋅ dm + ω ⋅ ∫ ξ ⋅ dm
••
•
M A = ∫ dM A = y A ∫ ξ ⋅ dm − ω 2 ∫ ξ ⋅ η ⋅ dm + ω⋅ ∫ ξ 2 ⋅ dm −
••
− x A ∫ η ⋅ dm + ω
2
•
∫ ξ ⋅η ⋅ dm + ω ∫η
2
.
⋅ dm
Fasst man zusammen und beachtet, dass
(
)
m = ∫ dm und J A = ∫ ξ 2 + η 2 ⋅ dm = ∫ r 2 ⋅ dm
gilt, vereinfachen sich die Gleichungen zu
••
•
••
•
Fx = m ⋅ x A − ω 2 ∫ ξ ⋅ dm − ω ∫ η ⋅ dm
Fy = m ⋅ y A − ω 2 ∫ η ⋅ dm + ω ⋅ ∫ ξ ⋅ dm
••
••
•
M A = y A ∫ ξ ⋅ dm − x A ∫ η ⋅ dm + J A ⋅ ω
Diese Gleichungen gelten noch ganz allgemein für jeden beliebigen körperfesten
Bezugspunkt A . Zwei Arten diesen Bezugspunkt zu wählen kommt besondere
Bedeutung zu:
•
Wählt man den Bezugspunkt so, dass er mit dem Schwerpunkt zusammenfällt, so
verschwinden die statischen Momente. Die Grundgleichungen der Dynamik des
starren Körpers bezüglich des Schwerpunktes lauten daher
••
••
Fx = m ⋅ x S
•
Fy = m ⋅ y S
•
MS = JS ⋅ ω
.
Wird der körperfeste Drehpunkt in einem Inertialsystem festgehalten, so gilt
natürlich
••
xA = 0
und
••
yA = 0
.
Die Drehbewegung um einen festgehaltenen Drehpunkt A wird dann durch eine
einzige Gleichung
•
MA = JA ⋅ω
beschrieben. Die verbleibenden zwei Gleichungen gestatten dann die Berechnung
der Komponenten der Kraft, die vom Lager auf den Körper ausgeübt wird:
•
Fx = − m ⋅ ξ S ⋅ ω 2 − m ⋅ ω ⋅ η S
•
Fy = − m ⋅ η S ⋅ ω 2 + m ⋅ ω ⋅ ξ S
ξ S , η S .......... Schwerpunktkoordinaten bezüglich eines parallel verschobenen
Koordi-natensystems mit dem Ursprung in A
2.2.Das Massenträgheitsmoment und der Satz von Steiner
Das Massenträgheitsmoment bezüglich einer Drehachse durch den Punkt A ist durch
J A = ∫ r 2 ⋅ dm
definiert. Die Integration erstreckt sich dabei über den ganzen Körper.
Das Massenträgheitsmoment eines homogenen Zylinders um seine Achse:
Der Zylinder wird in Zylinderröhren der Wandstärke dr unterteilt. Für das
Massenträgheitsmoment einer solchen Zylinderröhre bezüglich der Zylinderachse gilt
wegen
dm = ρ ⋅ 2 rπ ⋅ L ⋅ dr
dJ z = r 2 ⋅ ρ ⋅ 2 rπ ⋅ L ⋅ dr
.
ρ ........ Dichte des Zylindermaterials
L ........ Zylinderlänge
Das gesamte Massenträgheitsmoment des Zylinders ergibt sich dann durch Integration
über alle Radien von Null bis zum Zylinderradius R :
R
1
1
J z = ∫ r 2 ⋅ ρ ⋅ 2rπ ⋅ L ⋅ dr = ρ ⋅ R 4π ⋅ L = mR 2
2
2
0
Jz =
.
1
⋅m⋅R2
2
m............... Zylindermasse
R ............... Zylinderradius
J z .............. Massenträgheitsmoment eines homogenen Zylinders bezüglich seiner Achse
Der Satz von Steiner:
Der Satz von Steiner gestattet die Berechnung des Massenträgheitsmoment bezüglich
einer beliebigen Drehachse, wenn das Massenträgheitsmoment bezüglich einer zu dieser
Drehachse parallelen Achse durch den Schwerpunkt bekannt ist.
Gemäß Definition gilt
J A = ∫ r 2 ⋅ dm .
Der Abstand r des Masseelementes dm von der Achse durch A lässt sich mit Hilfe des
Kosinussatzes durch den Abstand rS des Masseelementes vom Schwerpunkt ausdrücken
(siehe Skizze):
J A = ∫ rS ⋅ dm + a 2 ⋅ ∫ dm − 2 ⋅ a ⋅ ∫ ξ ⋅ dm
2
.
Der erste Term ist das Massenträgheitsmoment bezüglich der Schwerachse. Der letzte
Term ist Null
Da das statische Moment um die um die η −Achse ist Null, der letzte Term
verschwindet daher. Zusammenfassend gilt:
J A = JS + m⋅ a2
J A ............. Massenträgheitsmoment bezüglich einer Drehachse durch A
J S .............. Massenträgheitsmoment bezüglich einer parallelen Achse durch den
Körperschwerpunkt
m............... Masse des Körpers
a ............... Abstand der beiden parallelen Drehachsen
Massenträgheitsmoment zusammengesetzter Körper:
Wenn ein Körper sich aus Teilkörper zusammensetzt, deren Massenträgheitsmoment
bekannt ist, ergibt sich das Massenträgheitsmoment durch Addition der
Massenträgheitsmomente der Teile. Dabei ist darauf zu achten, dass sich alle
Massenträgheitsmomente auf dieselbe Drehachse beziehen. Ist dies nicht der Fall, kann
der Satz von Steiner dabei helfen, die Massenträgheitsmomente vor der Addition auf
dieselbe Achse umzurechnen.
Trägheitsradius:
Denkt man sich den Körper durch eine Punktmasse im Abstand i von einer
Schwerachse ersetzt, so bleibt das Massenträgheitsmoment ungeändert, wenn
JS = m ⋅i 2
gilt. Dieser Abstand i ist der Trägheitsradius bezüglich dieser Schwerachse:
i=
JS
m
.
2.3.Arbeitsplan
Die Aufgaben der Kinetik lassen sich im allgemeinen in einzelne Teilaufgaben
untergliedern:
…
Identifizieren der Teile des mechanischen System und Freimachen dieser Teile
…
Aufstellen kinematischer Beziehungen: Verschiedene Bewegungsmöglichkeiten
sind oft nicht unabhängig voneinander!
Für die praktische Durchführung von Berechnung sind in jedem Fall positive
Koordinatenrichtungen für
• den Weg und damit die Geschwindigkeit und die Beschleunigung
• den
Winkel und damit die Winkelgeschwindigkeit und die
Winkelbeschleunigung
zu wählen (in die Skizze einzeichnen!)
…
Aufstellen der dynamischen Grundgleichungen für die Systemteile
…
Lösen des Gleichungssystems
Die Beispiele zur Starrkörperkinetik lassen sich in zwei Gruppen einteilen:
a. Beispiele bei denen keine Drehbewegung auftritt: der Momentensatz reduziert sich
dann auf die Momentenbilanz der Statik. Als Drehachse ist aber immer die
Schwerachse zu wählen.
b. Beispiele bei denen eine Drehbewegung auftritt.
Alle Aufgaben sollten daraufhin untersucht werden, welcher dieser beiden Fälle
vorliegt. Lässt sich die Bewegung auch als Bewegung eines Massepunktes beschreiben?
2.3.Die Kinetik der räumlichen Bewegung
Ein starrer Körper, der sich im Raum bewegt, hat drei Translations- und drei Rotationsfreiheitsgrade. Für jeden dieser Freiheitsgrade ist eine Bewegungsgleichung erforderlich. Die
räumliche Bewegung eines Körpers wird durch sechs Bewegungsgleichungen beschrieben.
Der Schwerpunktsatz:
Der Schwerpunkt eines starren Körpers bewegt sich so, als ob die gesamte Masse in ihm
vereinigt wäre und die Resultierende aller äußeren Kräfte an ihm angreifen würde:
v
v
F = m⋅a
Der Schwerpunktsatz ändert seine Form gegenüber dem Schwerpunktsatz der ebenen
Bewegung nicht. In Komponenten geschrieben beinhaltet er aber jetzt drei Gleichungen.
Der Momentensatz:
Für den Fall einer allgemeinen dreidimensionalen Bewegung treten an Stelle des
Momentensatzes der ebenen Bewegung nun die folgenden drei nach dem Mathematiker Euler
benannten Gleichungen:
J x ⋅ ω x − (J y − J z ) ⋅ ω y ⋅ ω z = M x
•
•
J y ⋅ ω y − (J z − J x ) ⋅ ω z ⋅ ω x = M y
.
J z ⋅ ω z − (J x − J y ) ⋅ ω x ⋅ ω y = M z
•
x , y, z
Jx ,Jy ,Jz
Koordinaten: der Koordinatenursprung muss im Körperschwerpunkt liegen; als
Koordinatenachsen werden die Hauptträgheitsachsen des Körpers verwendet
Massenträgheitsmomente bezüglich der Hauptachsen x , y, z
ωx ,ω y ,ωz
Komponenten der Winkelgeschwindigkeit in x , y, z -Richtung
M x ; M Y ; M Z Moment der äußeren Kräfte um die x , y, z -Achse
Achtung: Die Gleichungen gelten in dieser Form nur, wenn als Koordinatensystem das
System der Trägheitshauptachsen gewählt wird.
Bei symmetrischen Körpern sind die Hauptträgheitsachsen mit den Symmetrieachsen
identisch.
Diese Gleichungen werden nach dem Schweizer Mathematiker Euler (1707 bis 1783) als
Eulersche Gleichungen bezeichnet.