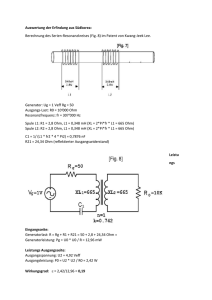
1 Elektronische Schaltung zur Auskopplung verstärkter Leistung in
Werbung

Elektronische Schaltung zur Auskopplung verstärkter Leistung in einem Resonanzkreis an eine Last http://worldwide.espacenet.com/publicationDetails/originalDocument?CC=US&NR=2008297134A1& KC=A1&FT=D&ND=3&date=20081204&DB=worldwide.espacenet.com&locale=en_CH Erfinder: Kwang-Jeek Lee, Seaoul, Südkorea Patentanmeldenummer: US 2008/02971,34A1 Anmeldedatum: Dec. 29, 2005 Veröffentlichungsdatum: Dec. 4, 2008 Übersetzt und kommentiert von A. Schneider, 18.2.2015 Der Erfinder hat im Prinzip eine ähnliche Schaltung wie Don Smith konzipiert, aber diese in die wesentlichen Komponenten aufgeteilt, ausführlich beschrieben und praktische Beispiele berechnet. Wie ersichtlich ist, unterteilt er die Schaltung in einen Ansteuerkreis 10, von dem über einen Serienwiderstand Steuerenergie geliefert und dem Resonanzkreis 20 aus C1 und L1 permanent zugeführt wird. Dieser Resonanzkreis soll laut Patent ein „Power Amplifier“ sein, also die Eigenschaft haben, zugeführte Leistung zu verstärken. Im Anschluss folgt ein Auskoppelkreis 30, der im Fall einer Teslaschaltung ein Step-Up-Transformer, im Falle praktischer Nutzung für den Haushalt ein Step-DownTransformer ist. Danach wird direkt – oder auch indirekt - die Nutzlast 40 ankoppelt. 1 Dass ein Schwingkreis als „Power Amplifier“ fungieren kann, ist in dieser Formulierung neu und bisher in der Elektrotechnik nicht bekannt. Ein üblicher Schwingkreis kann zwar zu grossen Amplitudenschwingungen (Spannung bzw. Strom) angeregt werden, doch normalerweise würde man erwarten, dass das Produkt aus angelegter Spannung undeingespeistem Strom, also die Leistung stets erhalten bleibt und wird nicht „verstärkt“ wird. Natürlich gilt,, dass die schwingende Blindleistung in einem Schwingkreis grösser ist, als die Leistung, mit der der Schwingkreis angeregt wird bzw. die verbrauchte Wirkleistung. Die Schwingkreisgüte, die ja sehr viel grösser als 1 sein kann, ergibt sich ja aus dem Verhältnis von zirkulierender Blindleistung zur aufgenommenden Wirkleistung, siehe http://de.wikipedia.org/wiki/G%C3%BCtefaktor In den im Patent dargestellten weiteren Abbildungen sind eine Vielzahl von Varianten der Schwingkreise, Ansteuerschaltungen und Lastschaltungen dargestellt. Interessanterweise wird der Resonanzkreis nicht über Diracimpulse angestossen, sondern mit einer klassischen Sinusschwingung bestimmter Frequenz. Es sei lediglich darauf zu achten, dass die auf die Primärseite reflektierte sekundäre Impedanz des Transformators relativ klein bleibt, so dass der Leistungsverstärler seine Resonanz aufrecht erhalten kann (und nicht zu stark gedämpft wird) – siehe Abschnitt [0010]. Im weiteren hier Auszüge aus dem Patent mit weiteren Kommentaren von mir in rot. Das eigentliche Ziel der Erfindung besteht laut Abschitt 0026 darin, den Stromverbrauch zu reduzieren, indem zwischen die Energiequelle und den Verbraucher ein leistungsverstärkender Resonanzkreis eingefügt wird. In Abschnitt [0028] wird die grundsätzliche Arbeitsweise beschrieben, wobei der Schwingkreis die Leistung verstärken soll und die zusätzliche Energie auch dort gepuffert wird, bevor sie kontinuierlich über den Auskoppeltransformator an die Nutzlast übertragen wird. In Abschnitt [0031] wird die eigentliche Arbeitsweise des Leistungsverstärker-Schwingkreises genauer beschrieben. Allerdings geht aus der Beschreibung nur hervor, dass der Power Amplifier die verstärkte Resonanzleistung bzw. Energie in der Induktivität der Primärspule speichert. Bei [0033] ist dargelegt, dass die Ausgangsleistung um das Q-fache verstärkt und nicht nur in der Induktivittäät, sondern auch in der Kapazität gespeichert wird und mit der Resonanzfrequenz hin- und herschwingt. In Abschnitt 0034 ist beschrieben, dass die verstärkte Leistung im Fall einer Serienresonanz der Qfachen Generatorspannung entspricht mal dem Strom im Schwingkreis. Für die Leistung im Schwingkreis gilt Ps = Q * Us*I0 . Da Us*I0 der angelegten Generatorwirkleistung entspricht (Strom und Spannnung sind in Phase, da der Serienwiderstand im Resonanzfall Null ist und nur der Generatorinnenwiderstand zum Tragen kommt, ergibt sich die Güte wie Bekannte aus dem Quotienten von Blindleistun Ps zur Wirkleistung Pw. In Abschnitt 0035 wird entsprechend dargelegt, dass im Fall einer Parallelresonanz der Strom um das Q—fache verstärkt wird und durch Multiplikation mit der Spannung die verstärkte Schwingkreisleistung darstellt. Laut Wikipedia http://de.wikipedia.org/wiki/G%C3%BCtefaktor ist die Leistung im Schwingkreis im Fall einer Serienresonanz definiert durch P = Q * R * I2 bzw. beim Parallelschwingkreis durch P = Q * U2/R. Das entspricht natürlich der Formel P = Q * I * U. Bei Schwingkreisen erreicht man maximal einen Q-Wert von bis zu 100:1. Somit hätte man also tatsächlich eine Leistungsverstärkung der Energie im Schwingkreis (!). Zum Vergleich. Bei Topfkreisen erreicht man Q = 200..300, be einem Quarz Q = 105, beim Laser 109, bei der Atomuhr 103. 2 In [0036] ist genauer spezifiziert, dass es sich natürlich bei der in der Induktivität gespeicherten Leistung um reine Blindleistung handelt. Der Grund liegt darin, dass Spannung und Strom fast um 90 Grad phasenverschoben sind. Diese Blindleistung pendelt zwischen Induktivität und Kondensator hinund her. In [003] und [0038] steht, dass die schwingende (um den Faktor Q verstärkte) Blindleistung über den Transformator (Sekundärspule) zur Nutzlast übertragen wird. Vorzugsweise sollte der Koppelfaktor k nahe bei 1 sein, also die Streufelder sollten so klein wir möglich gehalten werden. Auch das ist noch nachvollziehbar, dass also ein Trafo nicht nur Wirkleistung, sondern auch Scheinleistung übertragen kann. Solange auf der Sekundärseite kein Strom fliesst, errechnet sich gemäss [0039] die übertragene Spannung aufgrund des Windungsverhältniss n zu: U2 = k * U1/n = k * Q * Us/n Jetzt wird es spannend! Sobald Strom fliesst, bewirkt gemäss [0041] die zur Primärseite zurückgespiegelte Impedanz der Nutzlast, dass der Resonanzzustand beendet wird. Es kommt laut [0042] nun darauf an, die rückwirkende Impedanz möglichst klein zu halten, so dass die Schwingung auf der Primärseite nur wenig gedämpft wird! In der vorliegenden Erfindung ist eine Formel angegeben, um diese Rückwirkung gering zu halten. Daher erlaubt diese Methode gemäss [0042], das die verstärkte Leistung zur Nutzlast transformiert werden kann. Dies ist das eigentliche Revolutionäre der Erfindung, dass also in dieser Schaltung Blindleistung iin Wirkleistung transformiert wird!!! (Was noch zu testen wäre!). Laut [0043] kommt es darauf an, die reflektierte Impedanz Z21 richtig anzupassen. Vor allem muss der Widerstand R0 der Nutzlast optimal gewählt werden, damit die Schwingung auf der Primärseite aufrecht erhalten werden kann. Der „Trick“ besteht also darin, dass zwischen einer Stromquelle, z.B. einen Generator, und einer Last ein schwingender Resonanzkreis dazwischen geschaltet wird [0046]. Damit lässt sich laut Erfindung [0045] die übertragene Leistung verstärken. Hinweis von AS: Auf diese Weise ist es denkbar, dass auch die Rotoverter dadruch funktionieren, indem zur Motorunduktivität ein passender Kondensator zugefügt und damit ein Schwingkreis realisiert wird. Wenn Drehzahl und Schwingkreis zusammenpassen, nimmt der Motor weniger Leistung auf, gibt aber an den Generator eine höhere Leistung ab. Von der verstärkten Leistung kann dann ein Teil zum Motor zurückgeführt und das ganze System autonom betrieben werden, siehe auch unter www.borderlands.de/Links/Rotoverter.pdf In Fig 4b ist das Ersatzschaltbild eines Generators mit dem Quellwierstand Rg, dem parallel angeordneten Kondensator C1 und der Induktivität L1 samt Verlustwidersand R1 dargestellt. Die in der Spule schwingende Leistung beträgt P1 = U1 * I0 = Q * U2g/Rg . Der Strom ist hier der Resonanzstrom I0 = Ug/Rg . Hier ist nur der reelle Widerstand Rg wirksam, weil der Widerstand des Parallelschwingkreises Null ist. Fig. 4a zeigt das Ersatzschaltbild des Serienresonanzkreises. Hier ist die vom Generator abgegebene Leistung Pg = Ug * I0 = U2g/Rg. Die im Schwingkreis schwingende Leistung ist um den Gütefaktor höher, also P1 = Qs * Pg. 3 Wenn wir von einem idealen Transformator ohne Ohmsche Verluste ausgehen, ergibt sich auf der Sekundärseite eine Leistung von: P 2 = U 2 * I 2 = k2 * P 1 Der Koppelfaktor k (<1) geht hier quadratisch ein, weil der sowohl für die Spannung als auch für den Strom definiert ist. D.H. es gilt U2 = k * U1/n sowie I2 = k * n * I1 . Wenn n > 1 ist, wird die Spannung runter- und der Strom rauftransformiert und vice versa für n<1. Da wir aber einen realen Ausgangs-Lastwiderstand R0 haben und einen realen Generatorwiderstand Rg ergibt sich auf der Primärseite die sichtbare Impedanz zu: Z 21 = R21 + jX21 (in Ohm). [0054]. Das linke Ersatzschaltbild stellt die Situation dar, wie sie sich auf der Generatorseite ergibt, das rechte Ersatzschaltbild zeigt die Situation von der Sekundärseite aus betrachtet. In Fig 7. Ist ein Transformator mit Primär- und Sekundärspule dargestellt, die um einen Ferritkern gewickelt sind mit einer Induktivität von jeweils 348 mH und einem Widerstand von je 2,8 Ohm. Das Übersetzungsverhältnis ist n = 1. Der Kopplungskoeffizient wurde zu 0,742 gemessen. Die Serienresonanzfrequenz in Verbindung mit dem Schwingkreiskondensator beträgt 304 kHz. 4 Der Quellimpedanz des Signalgenerators Tektronix CFG 280 beträgt 50 Ohm. Der Signalgenerator wird genau mit der Serienresonanzfreqeuzn betrieben. Als Oszilloskop dient ein TDS 220, mit dem die Spannungen dargestellt werden [0059, 0060]. Fig.9 zeigt die äquivalenten Schaltkreise auf der Primär- und Sekundärseite, wobei hier auch die Spulenwiderstände mit berücksichtigt sind. Auf der linken Seite errechnet sich der totale Wirkwiderstand zu RT = Rg + R1 + R21 . Die SchwingkreisGüte ergibt sich dann zu Q s = XL1/RRT, also aus dem Verhältnis von Blindwiderstand zu Wirkwidestand der Spule, siehe: http://de.wikipedia.org/wiki/G%C3%BCtefaktor Das heisst, je kleiner der auf die Primärseite reflektierte Widerstand ausfällt, desto besser ist die Güte und damit die Leistungsverstärkung. Es ist daher zweckmässig, den Ausgangswiderstand relativ hochohmig auszuführen. Damit am Ausgang auch genügend Leistung verfügbar wird, sollte dann eine entsprechend hohe Spannung wirksam sein, denn P = U2 / R. Mit U = 3‘000 V und R = 10 kOhm lassen sich z.B. (nur oder immerhin) 900 W auskoppeln. Bei einem Q = 10, muss man dann auf der Primärseite nur 90 W einkoppeln. Die am Oszilloskop gemessenen Spannungen sind dann [0062]: Primärseite: U 1 = Qs * U g 5 Sekundärseite: U2 = (Qs/n) * k * Ug Falls der Kopplungskoeffizient k=1 wäre und das Windungsverhältnis n = 1, wird die Sekundärspannung genau dem Q-fachen Wert der Generatorspannung entsprechen. Andererseits wird der Sekundärstrom im Fall von k = 1 und n = 1 gleich dem Primärstrom sein. Somit errechnet sich die übertragene Leistung zu: P2 = U2 * I2 = Ug *Qs / n * k * k * n * I1 = Qs * k2 * P1 Die Nutzlast bezieht also die eigentliche Energie nicht vom Generator, sondern im wesentlichen von der im Resonanzkreis schwingenden (Blind-)Energie (jedenfalls wenn Q ordentlich hoch ist). Der Generator funktioniert im wesentlichen als Trigger für das Schwingungssystem. Daher wirken sich auch Laständerungen am Ausgang nur sehr geringfügig auf den Generator aus. Man könnte sagen, die Lenz’sche Regel gilt nur bedingt, oder die Back-EMF ist stark reduziert. Im Experimental-Schaltkreis in Fig. 9 A und 9 B errechnet sich [0066] bei einer Quellimpedanz von 50 Ohm und einem Lastwiderstand von 170 kOhm die induktive Impedanz XL1 zu 665 Ohm und XL2 zu 665 Ohm, wobei hier der Koppelfaktor k = 0,742 ist. Der reflektierte Widerstand ist R21 = 1,43 Ohm und damit deutlich kleiner als der Generator-Quellwiderstand von 50 Ohm. Daher wird die Schwingkreisgüte nur wenig beeinflusst. Nachdem auch der reflektierte kapazitive Blindanteil X21 = 5,6*0,001 = 0,0056 Ohm deutlich kleiner als der reflektierte induktive Blindwiderstand RL1 = 665 Ohm auf der Primärseite ist, kann der Resonanzzustand kontinuierlich auffrecht erhalten werden. Die totale reflektierte Impedanz Z21 errechnet sich nach folgender Formel R21 + jX21 in Ohm: Hierbei stellt M die Gegeninduktivität dar. Sie errechnet sich aus der Wurzel des Produktes der Primärinduktivitit und der Sekundärinduktivität, also M = SQR (L1*L2), siehe: http://tudresden.de/die_tu_dresden/fakultaeten/fakultaet_mathematik_und_naturwissenschaften/fachricht ung_physik/studium/lehrveranstaltungen/praktika/pdf/TR.pdf S. 3 . Der Streufaktor ist = 1 – M2/(L1*L2) und der Kopplungsfaktor k = SQR (1 – ) . 6 In der nachfolgenden Tabelle sind einige Messwerte aufgelistet, wenn das Ausgangssignal des Signalgenerators 1 V beträgt bei einem Quellwiderstand von 50 Ohm. Der Kopplungsfaktor k = 0,742. wurde vernachlässigt, weil weil R0 >> XL2 ist. [0069] Interessant ist, dass auch bei einer Last von 10 kOhm am Ausgang die Güte und damit der Verstärkungsfaktor von der ausgekoppelten Generatorenergie zur Ausgangsenerige von 2,42 mW mit Q = 6,56 noch recht ordentlich ist. Gleichzeitig ist erkennbar, dass mit kleinen Spannungen keine grossen Leistungen zu realisieren sind. Wenn der Ausgangsstrom I2 = 0 ist, also die Last unendlich, errechnet sich die Güte des Schwingkreises zu Qs = XL1 / (Rg + R1). Im vorgestellten Beispiel gilt Qs = 665 Ohm/ 52,8 Ohm = 12,59. Dabei ist der Quellwiderstand zu 50 Ohm angenommen und der Spulenwiderstand r zu 2,8 Ohm. Da ein Lastwiderstand von 1 MOhm nahezu unendlich ist, sollte eigentlich Qs für diesen Fall den Wert 12,59 erreichen. Tatsächlich wurde aber nur ein Wert von 8,59 gemessen. Es zeigt sich, dass die Güte eben nicht nur vom Ohmschen Widerstand, wie er bei Gleichstrom gemessen wird, abhängt, sondern auch vom Widerstand bei HF. Der effektiv wirksame Widerstand lässt sich indirekt berechnen aus Reff = XL1 / Qs = 667 Ohm/8,97 = 74,1 Ohm. Dieser Wert ist dem Quellwiderstand von 50 Ohm gegenüberzustellen. In Tab. 1 ist daher der Gütefaktor Qs dargestellt in Abhängigkeit vom Lastwiderstand R. Der Gütefaktor errechnet sich zu: Qs = XL1 / (Reff + R21) Wenn der Lastwiderstand z.B. 1,2 kOhm beträgt, ergibt sich ein reflektierter Widerstand zu 202,89 Ohm und die Spannungsverstärkung liegt bei 2,4. Ein Schaltkreis nach diesem Prinzip wird daher so betrieben, dass bei zunehmendem Lastwiderstand der reflektierte Widerstand und die reflektierte Impedanz abnehmen, während gleichzeitig der Gütefaktor Q und damit der Verstärkungsfaktor der Leistung ansteigt. In Tabelle 2 sind die Werte berechnet, wenn als Koppelfaktor 1 angenommen wird entsprechend dem Schaltbild in Fig. 8. Hinweis V2 muss hier mit k = 1 natürlich = V1 sein (nicht 0,742 V1, das ist ein Schreibfehler in der Tabelle). 7 Tabelle 3 zeigt, wie der Unterschied der ausgekoppelten Leistung ist, wenn die Nutzlast R 0 direkt an den Generator angeschaltet wird im Vergleich zur zwischengeschalteten Resonanzverstärkung. Falls der Lastwiderstand 10 kOhm beträgt, ist mit Leistungsverstärkung gemäss Tabelle 1 die auskoppelbare Leistung 2,42 mW, während sie bei direktem Anschluss des Lastwiderstandes an den Generator nur 0,1 mW beträgt. Die Verstärkung beträgt somit im Vergleich das 24,2fache. 8 Wenn man statt einem Koppelfaktor k=0,742 eine ideale Kopplung mit k = 1 annimmt, stehen mit Leistungsverstärkung 3,158 mW zur Verfügung, d.h. 31,58 mal mehr. Im nachfolgenden [0082] wird ein Schaltkreis mit Parallelresonanz beschrieben, und es werden die experimentallen Ergebnisse wiedergegeben. In Fig. 11 und Fig. 12 ist eine Schaltung dargestellt, bei der eine Eingangsspannung von 6,6 kV auf einen Parallelresonanzkreis eingekoppelt wird, wobei der Ausgangswiderstand am Sekundärkreis des Step-Down-Transformators den Wert R0 = 1 Ohm hat. Die Ausgangsspannnung U2 soll 220 V sein, so dass übliche ohmsche Verbraucher, z.B. Lampen, angeschaltet werden können. In Fig. 13 ist statt der Spannungsquelle von 6,6 kV eine Stromquelle dargestellt, die auf einen angepassten Widerstand R1 arbeitet. Der Gütefaktor errechnet sich bei diesem Parallel-Schwingkreis – siehe weiter unten - zu 8,58, wobei der Quellwiderstand vernachlässigt ist. Das Windungsverhältnis ist n = 30, wobei ein Koppelfaktor k=1 angenommen wird. 9 Der Blindwiderstand auf der Sekundärseite sollte 1% des Lastwiderstandes betragen, z.B. 0,0105 Ohm. Da das Verhältnis der Blindwiderstände X1 auf der Primärseite und X2 auf der Sekundärseite dem Quadrat des Windungsverhältnisses entspricht, gilt für den reflektierten Blindwiderstand auf der Primärseite XL1 = 302 XL2 = 900 * 0,0105 Ohm = 9,44 Ohm. Dieser Wert ist sehr klein und beeinflusst den Primärkreis kaum [0086]. Der reflektierte Scheinwiderstand ist Z21 = -(sM)2/Z22 = R21 + jX21 = 0,1 – j0,01 Ohm. Er ist so gering, dass er kaum einen Einfluss auf die Primärseite ausübt. Bei einem Spulenwiderstand R1 = 1 Ohm errechnet sich die Güte des Parallelschwingkreises zu Q = XL1 / Reff = 9,44 Ohm / 1,1 Ohm = 8,58, wobei Reff = RL1 + R21 gesetzt ist. Der wirksame Widerstand im Parallel-Resonanzkreis errechnet sich zu R1 = 81 Ohm. Er berechnet sich aus Reff*Q2 = 1,1 Ohm * (8,58)2. Der Quellwiderstand des Generators ist nicht berücksichtigt. In Fig. 13 ist die Spannungsquelle aus Fig. 11 bzw. Fig. 12 durch eine Stromquelle ersetzt, wobei im Resonanzfall (nur) ein Strom von 6,6 kV/81 Ohm = 81,5 A aus der Stromquelle gezogen wird. Im primären Blindwiderstand kann dagegen ein Strom zirkulieren, der entsprechend dem Gütefaktor um das 8,58fache grösser ist, also 699 A beträgt. Die primäre Resonanzleistung errechnet sich somit zu P1R = U1 * Qp * Io = 6,6 kV * 699 A = 4‘613 kW (also eine gewaltige Leistung !!!). Hinweis: Natürlich müssen die Bauteile entsprechend dimensioniert sein, um diese Spannungen und Ströme bewältigen zu können. Im Normalfall – ohne Leistungsverstärkung durch den Schwingkreis – müsste der Quellgenerator eine Leistung von 4,613 kW anbieten, die dann vom Transformator normal übertragen werden kann [0092]. Wenn aber das System in Parallelresonanz betrieben wird, muss der Stromgenerator nur eine Leistung von U1 * I0 = 6,6 kV * 81,5 A, also 537,9 kW zur Verfügung stellen. Das ist eben nur ein 1/8,58, ist also um das Verhältnis des Gütefaktors des Schwingkreises kleiner. Hinweis: Der im Text der Patentanmeldung angegebene Wert U1 * I0 = 6,6 kV * 0,0815 A, also 0,54 kW, ist eine Fehlrechnung (um den Faktor 1000 zu klein, Dimensionsfehle !!!). Aus dem Blickwinkel des Quellgenerators wird somit die Leistung verstärkt. Die gleichen Verstärkungseigenschaften können auch mit einem Serienresonanzkreis erzielt werden mit entsprechend angepassten Bauelementen. Verstärkerschaltung für Heimanwendungen Im weiteren wird in der Patentanmeldung ein zusätzliches Beispiel einer Verstärkerschaltung mit Parallelschwingkreis angegeben, die an einer Netzspannung von 220 V betrieben wird. Der Ausgang wird auf ein Netzgerät (hier nicht eingezeichnet) geschaltet, das 6 V Spannung und 0,3 A abgibt, also einen äquivalvalenten Lastwiderstand von 20 Ohm darstellt. Der sekundäre Blindwiderstand wird mit XL2 = 0,2 Ohm gewählt, damit 99% der Leistung an die Last von 20 Ohm übertragen werden kann. Das Windungsverhältnis errechnet sich zu n = 36,72 (220 V / 6 V), der primäre Blindwiderstand zu XL1 = 269 Ohm (n2 * XL2 = 36,72 * 0,2 Ohm,). 10 Im nachfolgenden Bild Fig. 15 ist dieselbe Schaltung dargestellt,, lediglich mit einer Stromquelle statt einer Spannungsquelle und dem Widerstand R1, durch den der Strom von der Stromquelle fliesst. Der Gütefaktor errrechnt sich hier zu Q p = XL1 / (RL1 + R21) = 269 Ohm / (40 + 27) Ohm = 6,3. Der primär wirksame Widerstand R1 ergibt sich zu R1 = (RL1 + R21)* Qp2 =42,7*6,3 = 1694,7 Ohm. Somit errechnet sich der von der Stromquelle fliessende Strom zu I 0 = U1/R1 = 220 V/1694,7 Ohm = 129,8 mA. Der im Parallelschwingkreis zirkulierende Strom ergibt sich zu Ip = Qp * Io = 6,3 + 129,8 mA = 818 mA. Bei einem Kopplungskoeffizienten von k=1 und dem angegebenen Windungsverhältnis errechnet sich der Ausgangsstrom zu I2 = n * IQ = 36,7 * 818 mA = 30 A. Dieser Schaltkreis verbraucht somit um den Gütefaktor 6,3 weniger Leistung auf der Primärseite im Vergleich zur Situation, wenn man die Ausgangslast über eine normalen Ubertrager direkt an das Netz anschliessen würde, also zusätzlichen Parallelschwingkreis. Industrielle Anwandungsmöglichkeiten Wenn zwischen einen Verbraucher und eine Stromquelle ein geeigneter Parallel- oder Serialresonankreis mit Übertrager geschaltet wird, lässt sich der Elektrizitätsverbrauch entsprechend dem Gütefaktor der Schwingschaltung reduzieren und somit Energie einsparen. Die Stromquelle dient in diesem 11 Fall mehr oder weniger nur dazu, den Schwingkreiss anzuregen, hat also primär eine steuerende Funktion. Bemerkung: In der ganzen Patentannmeldung wird wiederholt beschrieben, dass der Schwingkreis die angekoppelte Leistung bzw. die Triggerleistung verstärkt und zum Ausgang transfomiert. Es wird jedoch nirgends näher diskutiert, von wo eigentlich diese Zusatzleistung kommt. Als Black Box betrachtet, sieht es so aus, wie wenn elektrische Leistung aus den Nichts (natürlich aus dem Schwingkreis) generiert wird, was aber eigentlich dem Energieerhaltungssatz im klassischen Sinne widersprechen würde, jedenfalls wenn man – wie hier – davon ausgeht, dass die schwingende Blindleistung vom Trafo übertragen und am Ausgang in Wirkleistung umgesetzt wird. Das Problem lässt sich nur lösen, indem der ganze Schaltkreis mit Generator und Last nicht als geschlossenes System, sondern als offenes System betrachtet wird. In diesem Fall wäre das Resonanzsystem in der Lage, Energie aus der Umgebung aufzusaugen. Da für die Funktion weder eine Antenne noch eine Erdleitung erforderlich ist, kann die Energie nur aus dem Raum, z.B. aus der Luft, sprich aus den stets vorhandenen freien Elektronen (ionen) oder – im Weltall jedenfalls – direkt aus dem Quantenvakuum absorbiert werden. Dies ist natürlich eine zutiefst „philosophische“ Frage, wurde aber schon mehrfach von Physikern – nicht nur von Prof. Dr. Claus Turtur – ausgiebig diskutiert. So hat z.B. der theoretische Physiker Prof. Louis-Victor de Broglie, Nobelpreisträger für die Theorie der Materiwellen – siehe unter http://de.wikipedia.org/wiki/Louis_de_Broglie - darauf hingewiesen, dass die Schwankungen der Masse einzelner Teilchen und damit deren Energie als Folge des ständigen Energieaustausches mit dem subquantischen Milieu (Quantenfeld, Vakuumfeld) zu interpretieren ist. Laut Prof. Popescu ist daher die Wirkung bei Resonanz-Impulssystemen (das sind mechanische Resonanzverstärker ähnlich wie die elektrischen) mit der sog.. Freien Energie verknüpft – siehe „Der Quantum Energy Generator“ von Adolf und Inge Schneider, S. 62 unten. Patentansprüche Vor der Auflistung der eigentlichen Patentansprüche wird betont, dass die Erfindung nicht nur die hier diskutierten Beispiele umfasst, sondern auch alle möglichen denkbaren Variationen. Kommentar von AS: Es ist natürlich fraglich, ob die in der Anmeldung beschriebenen Grundlagen (Resonanzkreis mit Trafokopplung und geeeigneter Dimensionierung) überhaupt erfindungswürdig sind, weil es sich letztlich um völlig bekannte Schaltkreise und Phänomene der Elektrotechnik handelt. Ob die in der Anmeldung bzw. in den fünf Ansprüchen angegebenen Hinweise zur erfolgreichen Dimensionierung für die Erteilung eines Patentes ausreichen, ist fraglich. Letztlich kommt es nur darauf an, dass die Last am Ausgang des Schaltkreises so gewählt wird, dass der Schwingungszustand nicht wesentlich beeinträchtigt wird. Sofern diese Bedingung erfüllt ist, funktioniert das Prinzip – aber nach völlig klassischen Regeln der Elektrotechnik (wennngleich die Erklärung, wie und warum hier zusätzliche Energie eingekoppelt wird bzw. wie Blindleistung in Wirkleistung umgewandelt wird, in den klassischen Energieformeln nicht enthalten ist). Schluss-Resümee: Die in dieser Erfindung offen gelegten Erkenntnisse betreffen eigentlich nicht nur elektrische Schaltkreise, sonder lassen sich auf alle Gebiete der Physik (mechanische Systeme, magnetische Systeme, thermodynamische Systeme, optische Systeme usw.) erweitern. 12 So lassen sich z.B. auch Rotoverter erklären, wenn der Antriebsmotor durch eine passende Kapazität ergänzt wird, so dass der Motor nicht nur mechanisch dreht, sondern die Drehzahl auch zur Schwingungsfrequenz des LC-Kreises passt (ähnlich wie beim QEG). Dann nimmt der Motor weniger elektriche Leistung auf, als er an der Ausgangswelle - die direkt mit dem Generator gekoppelt ist (mechanische Kopplung statt elektriomagnetische Kopplung wie beim Transformator) - produziert. Das COPVerhältnis entspricht dann – von einigen Verlusten abgesehen – dem Gütefaktor des motorseitigen Schwingkreises, siehe hierzu www.borderlands.de/Links/Rotoverter.pdf . Immer wenn ein schwingungsfähiges System so aufgebaut wird, dass es in seiner Eigenfrequenz schwingen kann und die Last am Ausgang, die über ein Zwischenglied angekoppelt wird, nur geringfügig zurückwirkt, fliesst Energie (aus dem Umgebungsmedium, Vakuumfeld usw.) ein und verstärkt die am Eingang vorhandende, triggernde Primärenergie – laut Postulat des Erfinders. Die Grösse der Verstärkung ist eine direkte Funktion der Güte des Schwingkreises. Wenn nun schwingsfähige Systeme verwendet werden, die eine sehr hohe Güte aufweisen, z.B. Topfkreise, Schwingquarze, Laser usw., dann können sehr hohe Verstärkungen erzielt werden, siehe auch http://de.wikipedia.org/wiki/G%C3%BCtefaktor unter „Beispiele“. ETM3M hat z.B. mit einer integrierten Schaltung, innerhalb deren wohl ein Quarz integriert ist, einen Verstärkungsfaktor von 130‘000fach erzielen können, was wir (A.+I. Schneider) im Mai 2066 in der Unversität in Mexiko besichtigen und testen konnten (http://www.borderlands.de/net_pdf/NET0710S9-13.pdf). Es ist natürlich völlig klar, das bei ausreichend hoher Verstärkung ein Teil der Leistung von Ausgang auf den Eingang (direkt oder indirekt, z.B. gepuffert) zurückgeführt werden kann. Dann ist es möglich, ein Freies-Energie-System aufzubauen, dass – nach dem Start mit einer Hilfsenergiequelle – völlig autonom läuft. Schlusskommentar von A. Schneider Nachdem sich bei einer Patentrecherche gezeigt hat, dass es sich nicht nur um eine Patentanmeldung handelt, sondern dass der Erfinder auch unter der Nr. US8077485B2 das Patent erfolgreich erteilt bekommen hat (am 28. Dezember 2006), siehe: http://worldwide.espacenet.com/publicationDetails/originalDocument?FT=D&date=20111213&DB= worldwide.espacenet.com&locale=en_CH&CC=US&NR=8077485B2&KC=B2&ND=4 muss davon ausgegangen werden, dass die Patentbehörde – vielleicht auch durch Präsentation funktionierender Verstärkerschaltungen –die vorgeschlagenen Schaltungen (und alle denkbaren Variationen !?) patentwürdig sind und auch machbar sind. Wenn man diese Tatsache etwas eng – oder besser – weit auslegen würde, würde das konkret bedeuten, dass alle Systeme (mechanisch, elektrische, magnetisch, optische, atomare usw.), die auf der Basis eines Resonanzsystems aufgebaut sind, in dem (durch die Kreisgüte verstärkte) schwingende Blindleistung kumuliert und durch ein Kopplungselement (z.B. Übertrager o.a.) erfolgreich in Wirkleistung umgewandelt wird, durch obiges Patent abgedeckt. Wenn also jemand ein Freie-Energie-Gerät nach diesem Grundprinzip auf den Markt bringen möchte, müsste der Erfinder, ein Südkoreaner, entsprechend honoriert werden. Das ergäbe einen Billlionenmarkt und für den Erfinder sicher auch einige Milliarden. Vermutlich hat aber noch niemand – aussser vielleicht einem Industriekonzern in Südkorea – gemerkt, was hier dahintersteckt. 13