6 Die CMOS-Logik - antriebstechnik.fh

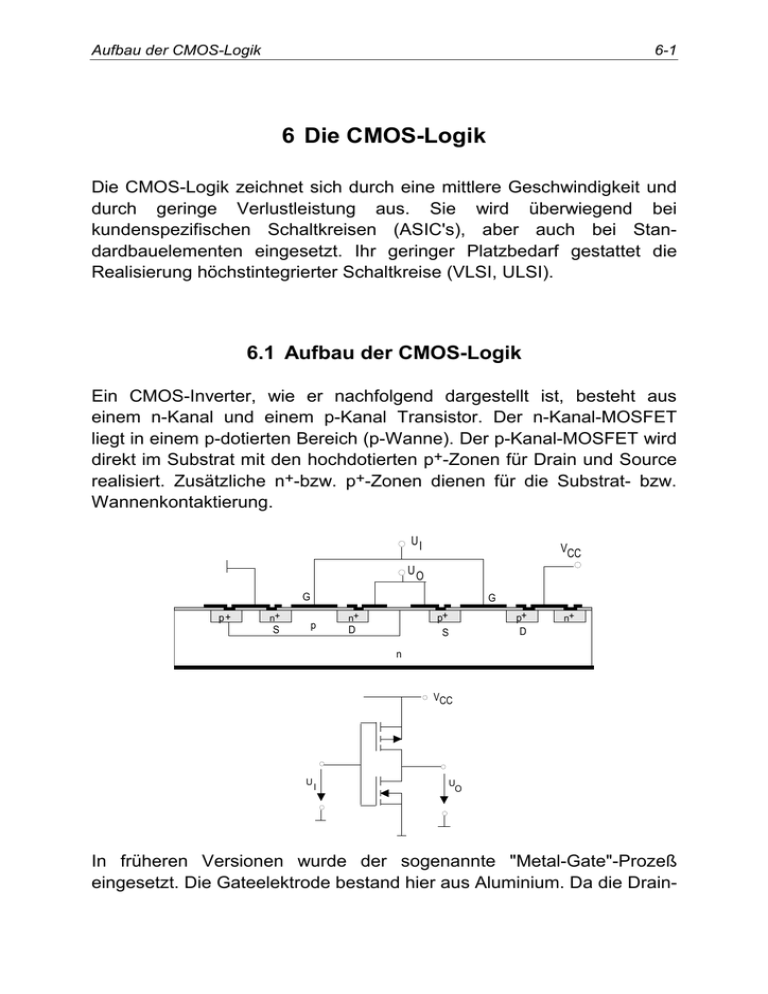
Aufbau der CMOS-Logik
6-1
6 Die CMOS-Logik
Die CMOS-Logik zeichnet sich durch eine mittlere Geschwindigkeit und
durch geringe Verlustleistung aus. Sie wird überwiegend bei
kundenspezifischen Schaltkreisen (ASIC's), aber auch bei Standardbauelementen eingesetzt. Ihr geringer Platzbedarf gestattet die
Realisierung höchstintegrierter Schaltkreise (VLSI, ULSI).
6.1 Aufbau der CMOS-Logik
Ein CMOS-Inverter, wie er nachfolgend dargestellt ist, besteht aus
einem n-Kanal und einem p-Kanal Transistor. Der n-Kanal-MOSFET
liegt in einem p-dotierten Bereich (p-Wanne). Der p-Kanal-MOSFET wird
direkt im Substrat mit den hochdotierten p+-Zonen für Drain und Source
realisiert. Zusätzliche n+-bzw. p+-Zonen dienen für die Substrat- bzw.
Wannenkontaktierung.
UI
VCC
UO
G
p+
n+
S
G
p
p+
S
n+
D
p+
D
n+
n
VCC
U
I
U
O
In früheren Versionen wurde der sogenannte "Metal-Gate"-Prozeß
eingesetzt. Die Gateelektrode bestand hier aus Aluminium. Da die Drain-
6-2
Die CMOS-Logik
und Sourcebereiche vor der Metallisierung hergestellt werden (Diffusion
bzw. Implantation), mußte die Al-Elektrode wegen eventueller Fehljustagen größer gewählt werden. Dies führte zu erhöhten Gate-DrainKapazitäten und schränkte die Geschwindigkeit ein. Außerdem erhöhte
sich dadurch die dynamische Verlustleistung.
Um diesen Nachteil zu vermeiden, wurde der "Polysilicon Gate"-Prozeß
entwickelt (1982). Die Gateelektrode wird jetzt anstatt aus Aluminium
aus Polysilizium hergestellt. Das Polysilizium kann vor der Implantation
der n+- bzw. p+-Bereiche für Drain und Source abgeschieden und
strukturiert werden und dient als Maske für den Dotierungsprozeß
(Selbstjustage). Die nachfolgende Abbildung zeigt einen Schnitt durch
den Inverter:
Poly-Gate
Metall
n+
n+
Feldoxid
p+
p+
p-Wanne
n-Substrat
Gateoxid
Heute existieren eine Reihe von CMOS-Technologien. Der Betriebsspannungsbereich verdeutlicht dies:
Familie
Spannungsbereich [V]
4000
3
- 15
4000 B
3
- 15
74 C
3
- 15
74 HC
2
- 6
74 HCT
4,5 - 5,5
74 AC
2
- 6
74 ACT
2
- 6
Der CMOS-Inverter
6-3
6.2 Der CMOS-Inverter
6.2.1 Prinzip des CMOS-Inverters
Eine ideale Logik sollte keine Verlustleistung und Verzögerungszeit bei
einer hohen Störsicherheit (50 % des Spannungshubes) aufweisen. Die
CMOS-Logik kommt diesen Forderungen sehr nahe.
Der prinzipielle
dargestellt:
Aufbau
eines
CMOS-Inverters
I
ist
nachfolgend
VCC
D
S
T
U
I
2
T
D
I D2
D
I D1
U
O
1
S
Er besteht aus zwei MOS-FET vom Anreicherungstyp (enhancement).
Der n-Kanal-Transistor hat die Aufgabe, bei einer logischen 0 am Ausgang diesen niederohmig mit Masse zu verbinden. Der p-KanalTransistor
verbindet
den
Ausgang
niederohmig
mit
der
Versorgungsspannung, wenn am Ausgang eine logische 1 liegt.
Bei der CMOS-Logik entspricht eine logische 1 der Versorgungsspannung VCC und eine logische 0 dem Potential der Masse.
6-4
Die CMOS-Logik
6.2.2 Schaltzustände
VCC
VCC
VCC
UGS1 = VCC
UGS2 = 0
ID
T2
ID
U0 @ 0
U0
T1
rDS1
ID
UGS1 = VCC
UGS2 = 0
U0
U0L
UI = VCC
rDS1 =
U0 = U0 L ≅ 0V
1
2K1(VCC − US )
VCC
Der CMOS-Inverter
6-5
VCC
VCC
UGS2 = -VCC
UGS1 = 0
ID
rDS1
T2
ID
UI
U0 @ VCC
U0
T1
ID
UGS2 = -VCC
UGS1 = 0
VCC
U0H
UI = 0V
U0 = U0H ≅ VCC
rDS 2 =
1
2K 2 (VCC − US )
U0
6-6
Die CMOS-Logik
Eigenschaften des CMOS-Inverters:
1.
Die Ausgangsspannungen bewegen sich zwischen 0 und VCC. Damit
wird der maximal mögliche Ausgangsspannungshub erreicht.
2.
Die statische Verlustleistung ist in beiden logischen Zuständen Null.
3.
Der Ausgang ist niederohmig gegen Masse oder VCC kurzgeschlossen.
4.
Der niederohmige Kurzschluß je nach logischem Zustand mit VCC
oder Masse erlaubt die Ansteuerung einer Vielzahl von weiteren
Stufen oder von Ausgängen.
5.
Der Eingangswiderstand ist unendlich. Deshalb kann ein Inverter
eine Vielzahl von weiteren Invertern ansteuern.
6.2.3 Der Umschaltvorgang
Liegt am Eingang eine Spannung UI = 0 V, dann ist die Gate-SourceSpannung des Transistors T1 ebenfalls 0 V (Schaltung Seite 6-3):
UI = UGS,1 = UGS,n = 0 V
Damit ist der Transistor T1 ausgeschaltet und ID1 = 0 A. Die GateSource-Spannung des p-Kanal-Transistors T2 ist:
UGS,2 = UGS,p = -VCC
Wenn VCC größer als die Schwellenspannung des Transistors T2
(US,2 = US,p) ist, bildet sich ein leitfähiger p-Kanal aus, und der Transistor
T2 verbindet den Ausgang mit VCC niederohmig. Wegen
ID1 = 0 = I D2
(kein Strom am Ausgang) ist die Ausgangsspannung im "High"-Zustand
(logische 1):
Der CMOS-Inverter
6-7
U0H = VCC
Liegt am Eingang eine Spannung UI = VCC, dann ist die Gate-SourceSpannung von Transistor T2
UGS,2 = UGS,p = 0 V.
Der Transistor T2 ist ausgeschaltet und ID2 = 0. Wenn VCC größer als
die Schwellenspannung von Transistor T1 ist (VCC > US,1 = US,n), dann
bildet sich in diesem Transistor ein leitender n-Kanal aus, und der
Ausgang ist niederohmig mit Masse verbunden. Wegen ID2 = 0 ist auch
ID1 = 0. Die Spannung am Ausgang bei einer logischen 1 am Eingang
ist:
U0L = 0.
Der Schaltvorgang wird durch die nachfolgende Abbildung verdeutlicht.
ID = ID1 = ID2
ID
p-K
p-Kanal
n-K
n-Kanal
U0
US
VCC
2
VCC-US
Im stationären Zustand (U0L, U0H) fließt nur ein extrem kleiner
Leckstrom. Damit ist die stationäre oder statische Verlustleistung
annähernd Null.
Die Spannungs-Transfercharakteristik bei langsamen Schaltvorgängen
(ohne Berücksichtigung von Umladeeffekten) ist nachfolgend dargestellt:
6-8
Die CMOS-Logik
UO
U =V
OH CC
0.5 VCC+ US
1
2
1 : T gesperrt
1
T2 Triodenber.
3 : T Sättigung
1
T Sättigung
2
2 : T Sättigung
1
T2 Triodenber.
4 : T Triodenber.
1
T2 Sättigung
3
0.5 VCC- US
UOL= 0
5 : T Triodenber.
1
T gesperrt
2
4
5
US UIL UIH
V
CC
0.5 VCC V - U
CC
S
UI
UDS = UGS -US
ID
Triode
Sättigung
UDS
Das Schaltverhalten soll unter folgenden vereinfachenden Voraussetzungen betrachtet werden:
1.
2.
3.
4.
5.
US,n = US,p = US
Kn = Kp = K
U-I-Charakteristik von T1 und T2 gleich
gleiche Gatekapazitäten pro Flächeneinheit C'0x
VCC > 2 US
Mit der Voraussetzung
µC0’ x  w 
Kn = K p; K =
 
2 L
gilt:
µ pC0’ x  w 
µ nC0’ x  w 
  =
 
2  L n
2  L p
Daher existiert die Bedingung
w 
 
 L  p µn
=
≅ 2,5
µp
w 
 
 L n
Der CMOS-Inverter
6-9
Für einen CMOS-Inverter mit gleicher Anstiegs- und Abfallzeit muß
w 
w 
deshalb   ≅ 1 und   ≅ 2,5 gelten.
 L n
 L p
Bereich (1) der Spannungstransfercharakteristik:
Für kleine Eingangsspannungen UI < US ist der n-Kanal-Transistor
ausgeschaltet (gesperrt). Der p-Kanal-Transistor ist im Triodenbereich
und U0 = U0H = VCC. Es fließt kein Drainstrom bis UI gleich US ist.
Sättigung oder Triodenbereich? :
Wenn UI > US ist, erreicht T1 Sättigung. T2 sättigt nicht, solange gilt
UDS < UGS - US
U DS, p < UGS, p − U S
Mit
U DS, p = VCC − U 0
und
UGS, p = VCC − U1
ergibt sich mit der
vorhergehenden Bedingung die dazugehörige Ausgangsspannung zu:
U0 > UI + US
Für Ausgangsspannungen größer als UI + US ist T2 nicht in Sättigung.
Dagegen ist der Transistor T1 in Sättigung für
U DS,n ≥ UGS,n − U S
Mit UDS,n = U0 und UGS,n = UI ergibt sich die Ausgangsspannung bei
Sättigung von T1 zu:
U0 ≥ UI − US
Bereich (3) der Spannungstransfercharakteristik:
VCC
V
− U S ≤ U 0 ≤ CC + U S
2
2
6-10
Die CMOS-Logik
Im Bereich (3) sind beide Transistoren gesättigt. Damit gilt für die
Drainströme:
I D1 = K (U I − U S )
2
n-Kanal
I D 2 = K (VCC − U I − U S )
2
p-Kanal
Ohne Last am Ausgang ergibt sich aus ID1 = ID2 die Eingangsspannung
bei Sättigung beider Transistoren zu:
1
U I = VCC
2
T1 ist in Sättigung für
U0 ≥
VCC
− US
2
T2 ist in Sättigung für
U0 ≤
VCC
+ US
2
Der Spannungsbereich, in dem beide Transistoren T1, T2 gesättigt sind,
ist damit:
VCC
V
− U S ≤ U 0 ≤ CC + U S
2
2
Zwischen diesen Ausgangsspannungen arbeiten zwei Stromquellen in
Serienschaltung. Der Inverter schaltet bei der halben Betriebsspannung.
Der Übergangsbereich (Bereich (3)) ist durch eine nahezu vertikale Linie
dargestellt, was auf eine sehr hohe Verstärkung schließen läßt. Dadurch
wird eine hohe Störsicherheit erreicht.
Bereich (2) der Spannungstransfercharakteristik:
In diesem Bereich ist der Transistor T1 gesättigt. T2 ist im Triodenbereich. Für die Ströme gilt:
I D1 = K (UGS,n − U S )
2
Der CMOS-Inverter
6-11
ID2
2

U DS,p 

= 2K  (UGS , p − U S )U DS, p −
2 

Mit U DS,p = VCC − U 0 , UGS ,p = VCC − U und UGS ,n = U ergibt sich durch
Gleichsetzen der beiden Ströme
U0 = UI + US +
(UI + US )2 + VCC (VCC − 2UI − 2US ) − (UI − US )2
Für die Berechnung von UIL setzt man die Ableitung der Ausgangsspannung nach der Eingangsspannung gleich -1 und erhält:
UI L =
3VCC + 2U S
8
Bereich (4) der Spannungstransfercharakteristik:
Ähnlich wie für den Bereich (2) kann man im Bereich (4) die Eingangsspannung für den "High"-Zustand berechnen:
U IH =
5VCC − 2U S
8
Bereich (5) der Spannungstransfercharakteristik:
Wenn UI größer als VCC - |US| ist, schaltet der Transistor T2 ab. Damit
wird ID1 = ID2 = 0. T1 ist im Triodenbereich und die Ausgangsspannung
ist
U0 = U0L = 0 V.
Beim Umschalten des Inverters fließt kein Strom im Bereich:
UI < US
oder
VCC - UI < US
6-12
Die CMOS-Logik
ID
I D, max
UI
0.5 V
CC
US
VCC- US
K D,max = K (0,5VCC − U S )
2
In der nachfolgenden Tabelle sind die charakteristischen Daten eines
Umschaltvorganges zusammengefaßt.
Bereich
1
Eingangsspannungsbereich
0 V ≤ UI ≤ US
n-Kanal
p-Kanal-
Ausgangsspannung U0 [V]
Transistor
Transistor
VCC = 5 V, US = 1 V, U1 [V]
gesperrt
Trioden-
5V
bereich
1
U S ≤ U I ≤ VCC
2
Sättigung
3
1
U I = VCC
2
Sättigung
Sättigung
1,5 V ≤ U 0 ≤ 3,5 V
4
1
VCC ≤ U I ≤ VCC − U S
2
Trioden-
Sättigung
U I − 6U I − 15 V − 1 V
VCC − U S ≤ U I
Trioden-
gesperrt
0V
2
5
Trioden-
U I + 15 V − 6UI + 1 V
bereich
bereich
bereich
Der CMOS-Inverter
6-13
6.2.4 Die Verlustleistung eines CMOS-Inverters
Man unterscheidet die statische und die dynamische Verlustleistung.
Die statische Verlustleistung eines CMOS-Inverters:
In beiden Schaltzuständen (logische 1 und 0) fließt kein Strom (nur der
Leckstrom). Die statische Verlustleistung ist deshalb sehr klein (< 1 µW)
und kann sehr oft vernachlässigt werden (Pstat ≅ 0).
Die dynamische Verlustleistung eines CMOS-Inverters:
Ein Inverter treibt im allgemeinen über eine Leitung ein nachfolgendes
CMOS-Gatter. Die Kapazitäten der Transistoren T1 und T2, die Leitungskapazitäten und die Eingangskapazitäten des nachfolgenden CMOSGatters bilden die Kapazität C. Damit kann man für die Berechnung der
dynamischen Verlustleistung von folgendem Ersatzschaltbild ausgehen:
VCC
i
T1P
uI(t)
u0(t)
T2N
C
6-14
Die CMOS-Logik
uI
VCC
u0
t
t=0
VCC
0
Entladungsvorgang
t £0:
Ladungsvorgang
u0 = VCC
Zu diesem Zeitpunkt ist in einem Kondensator die Energie
WC =
1
2
CVCC
2
gespeichert.
Bei t = 0 geht die Eingangsspannung uI auf den Wert VCC über. T1P wird
abgeschaltet und T2 N angeschaltet. Der Transistor T2 N entlädt den
Kondensator. Am Ende des Entladungsvorganges ist die Ladung im
1
2
wird im Transistor T2 N
Kondensator Null. Die Energie WT2 N = CVCC
2
abgebaut.
WT2 N = WC =
1
2
CVCC
2
Im Abschaltvorgang ( uI geht von VCC auf 0 über) wird der Transistor T2 N
abgeschaltet und T1P angeschaltet. T1P lädt den Kondensator über den
Der CMOS-Inverter
6-15
Strom i aus der Stromversorgung. Die benötigte Energiemenge aus der
Spannungsversorgung ist:
W = ∫ VCC ⋅ i dt = VCC ∫ i dt = VCC ⋅ Q
Q ist die im Kondensator gespeicherte Ladung. Am Ende des Vorganges
ist Q = C VCC .
Die Energiemenge aus der Spannungsversorgung ist am Ende des
Vorganges
2
W = C VCC
.
Die Im Kondensator gespeicherte Energie am Ende des Vorganges ist
aber
WC =
1
2
C VCC
.
2
Daraus folgt, daß die Hälfte der Energie während des Ladungsvorganges im Transistor T1P verbraucht wurde
WT1P = W − WC
WT1P =
1
2
C VCC
2
In jedem Zyklus wird in den Transistoren die Energie
2
W = WT1P + WT2 P = C VCC
verbraucht.
Mit einer Schaltfrequenz von f Zyklen pro Sekunde ergibt sich für die
dynamische Verlustleistung
2
Pdyn = f C VCC
6-16
Die CMOS-Logik
Wegen der geringen statischen Verlustleistung kann beim CMOSInverter
2
P ≅ Pdyn = f C VCC
gesetzt werden.
6.2.5 Das dynamische Verhalten des CMOS-Inverters
VC
T1
iD1
iD2
uI(t)
u0(t)
T2
C
uI(t)
VCC
u0(t)
t
0
t=
VCC
VCC
2
0
tDHL
tDLH
t
Der CMOS-Inverter
iD2
VCC
UDS = UGS -US
F
ID2
0
6-17
i2
E
T2 UDS2
VCC-US
Triode
VCC
Sättigung
C
u0
u0=UDS2
Wenn UI von 0 auf VCC übergeht (t ≤ 0) ist die Spannung am
Kondensator U0 = VCC . Der Kondensator C ist geladen. Zum Zeitpunkt
t = 0 steigt UI auf VCC an. Der Transistor T1 wird sofort abgeschaltet. Von
diesem Zeitpunkt an wird die Ersatzschaltung nur noch durch den
Transistor T2 und die Kapazität C gebildet. Die Spannung U0 ist gleich
der Versorgungsspannung VCC (Punkt E). Der Transistor T2 ist in
Sättigung und leitet einen relativ hohen Strom. Dies gilt bis zum, Punkt
F. Unterhalb des Punktes F befindet sich der Transistor im
Triodenbereich (U0 ⟨(UGS 2 − US ) d.h. U0 ⟨(VCC − US )) .
Bis zum Übergang zum Triodenbereich (Punkt F) gilt:
I D 2 ⋅ t DHL1 = Q = C ∆U
I D 2 = K 2 (UGS − U S )2
UGS = VCC
K2 (VCC − US )2 ⋅ t DHL1 = C ⋅ (VCC − (VCC − US ))
t DHL1 =
C ⋅ US
K2 (VCC − US )2
Unterhalb des Punktes F (Triodenbereich) gilt:
i2 ⋅ dt = −C du0
1 2 ö
æ
i 2 = 2K 2 ç (U GS - U S )U DS - U DS
÷
è
ø
2
UGS = uI
UDS = u0
6-18
Die CMOS-Logik
1 ö
æ
i 2 = 2K 2 ç (VCC - U S )u 0 - u 02 ÷
è
2 ø
u =V
2
0
CC
2K 2t DHL 2
d u0
= ò
1 2
C
u 0 =VCC -US (V
u0
CC - US )u0 2
æ 3V - 4U S ö
C
× lnç CC
÷
2K 2 (VCC - U S ) è
VCC
ø
t DHL 2 =
Gesamte Abfallzeit t DHL
t DHL = t DHL1 + t DHL2
=
=
C US
K 2 (VCC - U S )
2
C
K 2 (VCC
0,8 C
K2VCC
C
2K 2 (VCC - U S )
æ 3VCC - 4U S ö
÷
VCC
è
ø
lnç
é US
1 æ 3V - 4U S ö ù
+ lnç CC
÷ú
ê
VCC
- U S ) ëVCC - U S 2 è
øû
Für US ≅ 0,2 VCC
t DHL =
+
(US = 1 V ) gilt
( K2 =
eµ n W
2d
⋅
L
)
Wegen der Symmetrie der Transistoren im CMOS Gatter ist t DLH = t DHL .
tD =
t DLH + t DHL
= t DHL
2
CMOS-Gatter
6-19
6.3 CMOS-Gatter
Bei CMOS-Gattern ist jeder Eingang mit n-Kanal- und p-Kanal-Transistoren verbunden. Aus der Kombination mehrerer Transistoren können
unterschiedliche Gatterfunktionen realisiert werden.
CMOS-NAND-Gatter (zwei Eingänge):
Das NAND-Gatter besteht aus zwei in Serie geschalteten n-KanalTransistoren (T1, T3), die mit zwei parallel arbeitenden p-KanalTransistoren (T2, T4) verbunden sind.
Liegen beide Eingänge A und B auf einem logischen Pegel 0, sind die
beiden p-Kanal-Transistoren leitend und die n-Kanal-Transistoren gesperrt. Dadurch ist die Ausgangsspannung annähernd gleich VCC, was
einer logischen 1 entspricht.
Ist nur einer der beiden Eingänge auf dem Potential einer logischen 0,
dann ist immer der entsprechende n-Kanal-Transistor gesperrt und der
Ausgang liegt auf dem logischen Pegel 1.
6-20
Die CMOS-Logik
Sind beide Eingänge auf dem Potential VCC (logische 1), dann sind die
p-Kanal-Transistoren gesperrt und die n-Kanal-Transistoren leitend. Die
Ausgangsspannung entspricht einer logischen 0.
CMOS-NOR -Gatter (zwei Eingänge):
Das NOR-Gatter ist dual zum NAND-Gatter. Hier liegen die n-KanalTreibertransistoren parallel, während die p-Kanal-Transistoren in Serie
liegen.
Wenn an einem Eingang eine logische 1 liegt, ist der dazugehörige pKanal-Transistor gesperrt und der n-Kanal-Transistor im Triodenbereich.
Dies ergibt am Ausgang eine logische 0. Wenn beide Eingänge auf
Masse liegen (logische 0), werden beide p-Kanal-Transistoren leitend
und die n-Kanal-Transistoren gesperrt. Die Ausgangsspannung ist dann
gleich VCC (logische 1).
CMOS-Gatter
6-21
Die Grundstruktur von CMOS-Gattern läßt sich durch ein „Pull-up“ und
ein „Pull-down“ Netzwerk beschreiben.
VCC
A
B
C
Pull-up
Netzwerk
(PUN)
Y
A
B
C
Pull-down
Netzwerk
(PDN)
Das Pull-down Netzwerk wird leitend für alle Eingänge die einen LOWAusgang erfordern. Der Ausgang wird auf Ground-Potential heruntergezogen (pull down). Damit gilt folgender Zusammenhang:
fPDN ( A, B,C....) = y
Gleichzeitig geht das Pull up Netzwerk in den Sperrbetrieb über, d.h. die
Verbindung zu VCC wird unterbrochen.
Andererseits führen alle Eingangskombinationen zu einem High-Ausgang (y = 1) die das Pull-up Netzwerk in einen Kurzschluß versetzen,
d.h.
fPUN ( A, B, C...) = y
Mit diesen Überlegungen kann man relativ einfach die logische Funktion
eines CMOS Gatters ermitteln.
6-22
Die CMOS-Logik
Beispiel: NOR-Gatter
VC
VC
A
A
PUN
B
B
Y
Y
A
PDN
B
Y
A
B
Y
A
PDN
B
A+B = y
y = A+B
VCC
A
A
PUN
B
Y
A⋅ B = y
B
Y
y = A+B
CMOS-Gatter
6-23
Beispiel:
VCC
A
B
C
D
Y
A
B
C
D
PDN:
y = A ⋅ (B + C ⋅ D )
y = A ⋅ (B + C ⋅ D)
PUN : y = A + (B × (C + D ))
= A × (B + C × D)
6-24
Die CMOS-Logik
6.4 Charakteristische Daten von CMOS Gattern
Man unterscheidet heute im wesentlichen zwischen der HCMOS (High
Speed CMOS) und der ACL (Advanced CMOS Logic). Die ACL erreicht
hinsichtlich ihrer Geschwindigkeit die Eigenschaften der "Advanced
Schottky TTL" Logik (z.B. 74 ALS). Die nachfolgende Tabelle stellt
verschiedene Technologien gegenüber.
CMOS
HCMOS
TTL
ACL
ALS
VCC
[V]
4,5
4,5
5
UOH
[V]
4,4
4,4
2,5
UIH
[V]
3,15
3,15
2
UOL
[V]
0,1
0,1
0,5
UIL
[V]
0,9
1,35
0,8
IOL
[mA]
4
24
8
IIL
[µA]
-1
-1
-100
IOH
[mA]
-4
-24
IIH
[µA]
1
1
20
td
[ns]
8
3
6
-0,4
Das Transmissionsgatter
6-25
6.5 Das Transmissionsgatter
Das Transmissionsgatter besteht aus einem n-Kanal und einem p-KanalMOS-Transistor, die zueinander parallel geschaltet sind und in Serie
zwischen Aus- und Eingängen von Gattern liegen.
Symbol
VCC
C
C
A
B
A
B
C
C
C
1
0
C
0
1
A und B leitend verbunden
A und B über gesperrte
Transistoren getrennt
6.5.1 Diskussion des Schaltverhaltens eines Transmissionsgatters
a) Zustand:
C = VCC ,
C=0
C
A
Uin = VCC
VCC
T1
T2
C = VCC
B
U0
6-26
Die CMOS-Logik
Uin = VCC , UDS = VCC − U0 ,
C = VCC ,
UGSp = −VCC
C=0
Bereich 1
Bereich 2
Bereich 3
− Usn ≤ U0 ≤ VCC
0 ≤ U0 ≤ USp
USp ≤ U0 ≤ VCC − Usn
n-MOS-Trans.(T2)
n-MOS-Trans.(T2)
n-MOS-Trans.(T2)
UDS = VCC − U0
UDS = VCC − U0
UDS = VCC − U0
UGSn = VCC − U0
Usn ≤ UDS ≤ VCC − USp
0 ≤ UDS ≤ USn
U DS ⟩U GSn − U sn
UGsn = VCC − U0
UGSn = VCC − U0
UDS ⟩ VGSn − Usn
0 ≤ UGSn ≤ USn
Sättigung
Sättigung
Sperrbetrieb
p-MOS-Trans. (T1)
p-MOS-Trans. (T1)
p-MOS-Trans.(T1)
UDS = −VCC + U0
−Usn ≤ UDS ≤ −VCC + USp
0 ≤ UDS ≤ Usn
UGSp = −VCC
UGSp = −VCC
UGSp = −VCC
UDS ⟩ UGSp − USp
UDS ≤ UGSp − USp
UDS ⟨ UGSp − USp
Sättigung
Triodenbereich
Triodenbereich
CC
Das Transmissionsgatter
6-27
A und B sind leitend miteinander verbunden. Für die Widerstände
zwischen A und B gilt:
Bereich 1
Rg = Rn Rp
Rn =
Rp =
(VCC − U0 )
Kn (VCC − U0 − USn )
VCC − U0
(
Kp VCC − USp
)
2
2
Bereich 2
Rg = Rn Rp
Rn =
Rp =
VCC − U0
Kn (VCC − U0 − USn )
2
1
[
]
Kp 2(VCC − USp ) − (VCC − U0 )
Bereich 3
Rg = R p =
[
1
]
K p 2(VCC − USp ) − (VCC − U0 )
6-28
Die CMOS-Logik
b) Zustand:
C = 0 , C = VCC
C = V CC
T1
A
Uin
T2
B
U0
C=0
Bereich 1
Uin = VCC ,
UDSn = VCC − U0 , UGSp = 0
p-MOS-Trans. (T1) ist gesperrt
UGSn = −U0
n-MOS-Trans. (T2) ist gesperrt
Bereich 2
Uin = 0 ,
UDSn = −U0 , UGSn = −U0
n-MOS-Trans. (T2) ist gesperrt
UGSp = +VCC
p-MOS-Trans. (T1) ist gesperrt
Es existiert keine leitende Verbindung zwischen A und B.
Das Transmissionsgatter
6-29
6.5.2 Beispiel für die Verwendung von Transmissionsgattern
C1
A
C1
Y
C2
B
C2
VCC
S
y = A ⋅S + B ⋅S
A
B
S
C1
C2
C1
C2
y
0
0
0
1
0
0
1
0
0
1
0
1
0
0
1
0
1
0
0
1
0
0
1
1
1
1
0
1
0
0
1
1
0
0
1
0
1
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
0
0
1
1
1
0
1
1
0
1
6-30
Die CMOS-Logik
6.6 BiCMOS-Logik
BiCMOS => Bipolar - CMOS - Logik
BiCMOS-Logik beinhaltet Bipolar- und CMOS-Schaltkreise in einem
Chip. Das Ziel ist die Kombination der Low-Power-Eigenschaften, des
hohen Eingangswiderstandes und des großen Spannungshubes der
CMOS-Logik mit der großen Stromtragfähigkeit der Bipolar-Transistoren.
Dies ist insbesondere wichtig bei relativ großen Lastkapazitäten
(Ausgangstreibern).
Prinzip:
VCC
T1
uI
T2
u0
Diese Schaltung hat den Nachteil, daß relativ lange Verzögerungszeiten
von T1 und T2 auftreten, weil die Basis nicht entladen werden kann. Aus
diesen Gründen werden die Widerstände zwischen den Basisanschlüssen und Masse eingeführt.
BiCMOS-Logik
6-31
VCC
T1
R1
uI
u0
T2
R2
Der Nachteil dieser Schaltung liegt in der benötigten statischen Verlustleistung. Dieser Nachteil wird durch die folgende Schaltung beseitigt:
VCC
T1
R1
uI
u0
T2
R2
CL
6-32
Die CMOS-Logik
td [ns]
CMOS
4
3
BICMOS
2
1
CL [pF]
1
2
3
4
5
BiCMOS-NAND-Gatter:
VCC
A
B
R1
Y = A·B
A
B
R2