R - Institut für Kernphysik

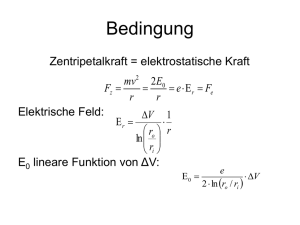
Kern- und Teilchenphysik
53030 Kern- und Teilchenphysik
Vorlesung
Di. 12.00-12.45 im Hörsaal III
Do. 10.00-11.30 im Hörsaal II
Übungen
Di. 12.45-13.30 im Hörsaal III, Leiter: Michael Seidlitz
Klausur
26.2.2014 Mi. 9:00-12:00 Hörsaal I
Web-page
http://www.ikp.uni-koeln.de/groups/reiter/lehre.html
Dozent
Peter Reiter, Institut für Kernphysik, Raum 306, Tel. 0221 4703624
Mail: [email protected]
Kern- und Teilchenphysik
Grundlegende Eigenschaften der Atomkerne:
• a-Zerfall
• Beispiele zum a-Zerfall
Zulassungskriterium zur Klausur ist 50% der Punkte für
die Übungsaufgaben.
a-Zerfall
Beim a-Zerfall wird ein a -Teilchen vom radioaktiven Kern emittiert.
Ordnungszahl (Atomzahl) um zwei (vier) Einheiten reduziert.
Energiedifferenz der Atommassen:
Q = M(Z,A) - M(Z - 2,A - 4) - M(4He)
= B(Z - 2;A - 4) + Ba(28,3 MeV) - B(Z;A):
Der Q-Wert einer Reaktion oder eines Zerfalles ist die verfügbare Energie, die
sich unter den beteiligten Teilchen als kinetische Energie aufteilt.
Hier ist Q also die kinetische Energie
des a 's und die Rückstossenergie des
Tochterkernes. Da Mutter- und Tochter
feste Massen haben sind a 's monoenergetisch mit kinetischen Energien von
einigen MeV (4 -10 MeV).
Aufnahme der Ionisationsdichte in einer
Nebelkammer. Spuren aus einer kollimierten
a -Quelle (214Po -> 210Pb + a). Die konstante
Länge der Spuren zeigt, dass die a 's
monoenergetisch sind (Q= 7.7 MeV).
a-Zerfall
Protonen und Neutronen sind auch in schweren Kernen mit bis zu 7 MeV gebunden,
und können daher nicht aus dem Kern entweichen. Die Emission eines gebundenen
Systems ist eher möglich, da zusätzlich Bindungsenergie zur Verfügung steht.
Von Bedeutung ist dies insbesondere für a-Teilchen, da sie eine außerordentlich große
Bindungsenergie von 7.1MeV/u haben.
Atomkerne besitzen eine Coulombbarriere, die ein sich im Kern formiertes Alphateilchen daran hindert, diesen zu verlassen. Das a-Teilchen müßte dazu eine potentielle
Energie besitzen, welche größer als das abstoßende Coulombpotential ist:
2( Z  2)e2 2( Z  2)ac
VCoul 

r
r
Klassisch ist es für E < Vcoul unmöglich,
diese Barriere zu überwinden; quantenmechanisch besteht eine gewisse Wahrscheinlichkeit für das a-Teilchen, die Barriere
und damit den klassisch verbotenen Bereich
zu durchdringen. Tunneleffekt.
Tunneleffekt Q.M. Wiederholung I
Quantenmechanik: Zeitunabhängige
Schrödingergleichung:
A
B
C
2 2

 ( x)  V ( x) ( x)  E ( x)
2m x 2
2
Normierungsbedingung :  dx ( x)  1
Für das positive Potenzial gibt es in der
klassischen Mechanik keine gebundenen
Zustände.
Betrachten nur Energien unterhalb der
Höhe der Barriere. In der klassischen
Physik wird ein Teilchen, das sich auf
die Barriere zubewegt, total reflektiert.
Es kann nicht in das Innere der Barriere
eindringen.
Quantenmechanik:
Allgemeiner Ansatz für Lösungen
in Gebieten A,B,C:
L
Tunneleffekt Q.M. Wiederholung II
Betrachte Teilchen das von links einläuft und
dann reflektiert und transmittiert wird.
A
B
C
• Im Gebiet C also nur eine nach rechts
laufende Welle => g-=0
• Normierung so, daß a+=1
L
Die Koeffizienten S und a- haben folgende
physikalische Bedeutung:
Betrachte den Teilchenstrom:
Für die ebenen Wellen in A und C gilt:
Die Wahrscheinlichkeiten für
Transmission und Reflexion:
Tunneleffekt Q.M. Wiederholung III
Betrachte Lösung in Bereichen A, B, C
A
B
C
L
Wie vorher nur für B Substitution k  i k
und Untersuchung der Anschlußbedingungen
Transmissionskoeffizienten T
2




k
k
2
0
1

T  1  4    sinh kL 


 k0 k 


1
Für große Barrieren kL>>1 gilt:
1
sinh 1  exp( 2kL)
4
 2L

T ( E )  const  exp  
2m(V0  E ) 
 

Die Transmissionswahrscheinlichkeit
T(E) ist nicht Null. Die Teilchen können
also die Barriere durchdringen. Dies ist
ein spezifisch quantenphysikalischer
Effekt, der in der klassischen Physik
keine Entsprechung hat.
Aufenthaltswahrscheinlichkeit:
 Y(x) 2
a-Zerfall und Tunneleffekt
Quantenmechanik: Tunnelwahrscheinlichkeit
läßt sich für ein endliches Kastenpotential
exakt berechnen:
 2L

T ( E )  exp  
2m(V0  E ) 
 

Für einen allgemeinen Potenzialberg ist dies
nicht möglich.
Näherungsformel: Zwischen den klassischen
Umkehrpunkten wird das Potential in n kleine
Schwellen der Breite Dx zerlegt.
x

 2 2


T ( E )   Ti ( E )  exp   dx
2m(V ( x )  E )  


i 1
 x1  

n
Annahmen:
- Exponentialfaktor ist wesentlich größer als
Eins
-WKB (Wentzel, Kramers, Brillouin) Näherung
für kontinuierliche Potentiale V(x)
L
a-Zerfall Zerfallswahrscheinlichkeit
Das α-Teilchen bewegt sich in einem mittleren
Potenzial V(r) im Tochterkern. Im Inneren des
Kern ist V0 konstant, außerhalb des Kernradius
R ist es ein reines Coulomb-Potenzial
Beispiel 238U (Vorgriff):
-V0 ~ -100 MeV R = ~ 10 fm
VC
L
Ansatz für die Zerfallswahrscheinlichkeit pro
Zeiteinheit λ:
λ=S·ω·P
• S Wahrscheinlichkeit daß sich bereits im
Kerninneren ein α-Teilchen formiert hat.
• ω Frequenz, mit der das Teilchen an die
Barriere stößt.
• P ist die Penetrabilität, die Wahrscheinlichkeit
für einen Tunnelprozess.
Ri
Ra
V0
Bemerkung:
Das α-Teilchen kann im Kern auch
Bahndrehimpuls l tragen. Diesen
Vernachlässigen wir im folgenden,
d.h. es gilt nur für Zerfälle zwischen
Grundzuständen mit l=0.
a-Zerfall Zerfallswahrscheinlichkeit
P ist die Penetrabilität,
Wahrscheinlichkeit für
Tunnelprozess:
Idee & Nebenrechnung:
P  e 2G mit Gamow Faktor G
G ( Ea ) 
Ra
1
dr
R  
i

2m(V ( r )  E ) 

2 Ze 2
mit V(Ra )  Eα 
Ra
R
a
2
2 Ze 2
G ( Ea ) 
2m  dr
E

r
Ri

2m
2
2 Ze arccos
Ea


R
E
beachte i  α
Ra Vc
2


Coulombpotential
Ausgedehnte Barriere
Ri

Ra
2
Ri Ri
 2
Ra Ra
für Eα  Vc bzw. Ra >> Ri gilt


arccos


Ri

Ra
2
Ri Ri

Ra Ra 2

 
 
2


Ri
Ra





a-Zerfall und Geiger-Nutall Gesetz
P  e 2G mit Gamow Faktor G
G ( Ea ) 
2


2m
2Ze2  
Ea
2
Ri 

Ra 
Für den Logarithmus der Zerfallskonstante gilt das Geiger-Nuttall’sche Gesetz:
Zusammenhang zwischen Halbwertszeit und Energie der a-Teilchen
ln λ  ln S - ln Dt - 2G(Ea)
Z
Z
 b( Z)  a
 a
Ea
Ea
S - a-Formation
Dt - Frequenz des a im Kern
P - Gamow-faktor

1

und
T1 / 2 
ln 2
 ln 2  

Geiger-Nutall Gesetz
a-Zerfallsreihen
Kurze Halbwertszeit
Neue chemische Elemente
17. November 2006
The name Roentgenium
is given to the element 111
in an official ceremony at GSI.
Stabilisierung durch
Schaleneffekte
Insel der
Stabilität
?
Z = 100
Tröpfchenmodell
Schwerstes anerkanntes chemisches Element Cn
Ordnungszahl:112, an der GSI entdeckt,
hat seit 19. Februar 2010 den offiziellen
Namen: Copernicium
Synthese and Identifikation von schweren Elementen
n
70Zn
208Pb
277112
277112
273110
VR
11.45 MeV
280 s
12 m
269Hs
265Sg
bekannt
kinematische Separation
im Fluge durch Vergleich
der elektrischen und
magnetischen Feldkraft
 Geschwindigkeitsfilter
257No
253Fm
8.34 MeV
15.0 s
Date: 09-Feb-1996
Time: 22:37 h
261Rf
8.52 MeV
4.7 s
11.08 MeV
110  s
9.23 MeV
19.7 s
4.60 MeV (escape)
7.4 s
Identifikation durch
sechs a-Zerfälle
a-a Korrelationen
(Ort und Zeit)
a-Zerfälle von zwei
bekannten Isotopen
Zusammenfassung
Weizsäcker Massenformel: Stabile, in der Natur vorkommende Kerne bilden
ein schmales Band in der N-Z-Ebene der Nuklidkarte.
Für sehr neutronenarme bzw. –reiche Kerne definiert die Bedingung Bn= 0 bzw.
Bp= 0 die sog. ´Abbruchkanten´.
Die Nuklide von Fe und Ni besitzen die höchste Bindungsenergie pro Nukleon.
Bedingung für einen Zweikörperzerfall: M(A,Z) > M(A-A´, Z-Z´)+M(A´,Z´)
a-Zerfall: Tunnelprozess durch die Coulombbarriere des Kernpotentials