Die geradlinig gleichförmige Bewegung

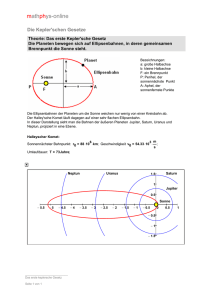
1.5 Himmelsmechanik
Gegen Ende des 15 Jahrhunderts setzte sich in Mitteleuropa eine radikale Änderung des Weltbildes
durch, die als sog. Kopernikanische Revolution bezeichnet wird. So behauptete Nikolaus Kopernikus,
dass sich nicht die Erde im Mittelpunkt des Universums befindet, sondern, dass die Erde und
sämtliche Planeten um die Sonne kreisen. Als erstem Mathematiker gelang es jedoch nicht
Kopernikus, sondern Johannes Kepler (1571-1630), die Bewegung der Himmelskörper mathematisch
mit drei Gesetzen zu beschreiben. In diesem Kapitel werden diese nach ihm benannten „Keplerschen
Gesetze“ der Planetenbewegung kurz vorgestellt.
[14] Johannes Kepler
Erstes Keplersches Gesetz:
Alle Planeten bewegen sich auf Ellipsenbahnen in deren einem Brennpunkt die Sonne steht. In
unserem Sonnensystem sind die Planetenbahnen nahezu kreisförmig.
Ellipseneigenschaften:
Ellipsen sind im mathematischen Sinne sog. Kegelschnitte. Diese erhält man, wenn man einen Kegel
zerschneidet. Führt man einen solchen Schnitt parallel zur Grundfläche aus, so erhält man die Fläche
eines Kreises (Spezialfall der Ellipse). Setzt man das Messer bildlich etwas schräg an, so wird aus der
Schnittfläche eine oval geformte Ellipse.


© M. Brennscheidt
und : Brennpunkte der Ellipse
: Große Halbachse


: Kleine Halbachse
: Lineare Exzentrizität (Abstand von einem Brennpunkt zum Mittelpunkt)
In einer Ellipse ist die Summe der Strecken
Halbachse und somit konstant.
und
immer gleich dem doppelten der großen
Ein Maß für die „Ovalität“ einer Ellipse ist die sog. Exzentrizität. Diese gibt an, wie weit die
Brennpunkte vom Mittelpunkt der Ellipse entfernt sind. Ist die lineare Exzentrizität gleich Null so
liegen beide Brennpunkte in einem Punkt und es liegt ein Kreis vor. Die lineare Exzentrizität kann mit
dem Satz des Pythagoras aus den beiden Halbachsen berechnet werden:
Neben der linearen Exzentrizität wird häufig auch die sog. numerische Exzentrizität angegeben. Diese
ist gegeben durch den Quotienten aus linearer Exzentrizität und großer Halbachse.
Die numerische Exzentrizität kann niemals größer als 1 werden, da die numerische Exzentrizität nicht
größer sein kann als die große Halbachse. Für
ist auch
und es liegt erneut der Spezialfall
Kreis vor.
Zweites Keplersches Gesetz (Flächensatz):
Der Fahrstrahl (Verbindungslinie Sonne-Planet) überstreicht in gleichen Zeiten gleiche Flächen!
Die Bahngeschwindigkeit der Planeten hat also im sonnennächsten Punkt, dem Perihel den größten
und im sonnenfernsten Punkt dem Aphel den kleinsten Betrag. Wenn also die Strecken und in
derselben Zeit
zurückgelegt werden, dann sind die Fläche
und
gleich groß:
Drittes Keplersches Gesetz:
© M. Brennscheidt
Die Quadrate der Umlaufzeiten
und
zweier Planeten verhalten sich wie die dritten Potenzen
der großen Halbachsen und ihrer Bahnen:
Die Konstante ist für alle Planeten eines Sonnensystems gleich und ist abhängig von der Masse des
Zentralsterns! Das dritte Keplersche Gesetz kann deshalb benutzt werden, um die Abstände der
Planteten von der Sonne (genauer die großen Halbachsen) zu bestimmen, indem man „lediglich“
deren Umlaufzeit misst:
Anmerkung: Alle drei Keplerschen Gesetze beruhen auf genauen astronomischen Messungen. Das
Aufstellen dieser Gesetze stellt eine physikalische und mathematische Meisterleistung dar, da die
astronomischen Fernrohre gegen Ende des 15. Jahrhunderts noch sehr unpräzise waren.
© M. Brennscheidt