Kepler-Gesetze
Werbung

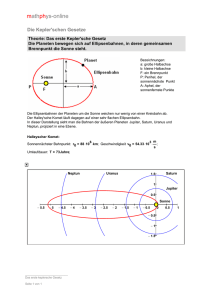
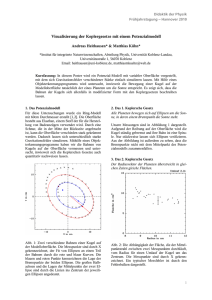
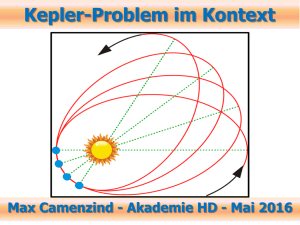
Walddörfer-Gymnasium Informatik MS-Word Kepler-Gesetze Kepler-Gesetze 1. Kepler-Gesetz: Trabanten bewegen sich auf Ellipsen, in deren einem Brennpunkt der Zentralkörper (Sonne, Erde) steht. b a Aphel 2e F Perihel F 1 2 Ellipsen haben eine große Achse, deren Hälfte die große Halbachse a genannt wird. Senkrecht dazu steht die kleine Achse mit der entsprechenden kleinen Halbachse b. Ein Kreis ist somit ein Spezialfall der Ellipse mit a = b = r. Die Strecke e wird lineare Exzentrizität genannt und wird im Spezialfall Kreis zu e = 0. Das Verhältnis e/a heißt numerische Exzentrizität und ist ein Maß für die Abweichung von der Kreisform. Langgestreckte Ellipsen haben eine numerische Exzentrizität von nahezu 1, bei Kreisen ist sie dagegen 0. F1 und F2 heißen Brennpunkte, weil die von ihnen ausgehenden Lichtstrahlen auf den jeweils anderen Brennpunkt reflektiert würden. 2. Kepler-Gesetz Der vom Zentralkörper zum Trabanten gezogene Fahrstrahl überstreicht in gleichen Zeiten gleiche Flächen. b a F1 2e F2 Aus dem Gesetz wird deutlich, dass die Geschwindigkeit des Trabanten mit zunehmender Entfernung vom Zentralkörper geringer wird. Newton konnte später dieses Verhalten durch Kräfte erklären. Teilt man die auf den Trabanten wirkende Kraft in Richtung des Fahrstrahls in seine tangentiale Komponente Ft und senkrecht zu Bahn stehende zentrale Komponente F z auf, so erkennt man: Fz verrichtet keine Arbeit und entfällt für die Betrachtung. Ft wirkt bremsend auf den Körper, wenn er sich vom Zentralkörper entfernt und wirkt beschleunigend bei Annäherung an den Zentralkörper. Übungsdatei „Kepler-Gesetze“ Seite 1 von 1