Digitale Signalverarbeitung

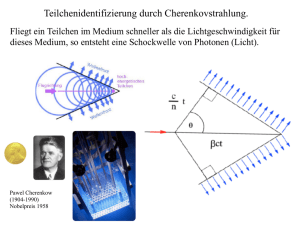
Westfälische Wilhelms-Universität Münster
Institut für Angewandte Physik
Experimentelle Übungen für Fortgeschrittene
Digitale Signalverarbeitung
Dezember 2006
In der Digitaltechnik ist es nicht möglich, physikalische Signale kontinuierlich zu bearbeiten,
wie dies in der Analogtechnik der Fall ist. Digitale Komponenten werden im Allgemeinen getaktet, d. h. es werden Zeitmarken ausgegeben, bei denen dann jeweils ein Arbeitsschritt pro Takt
ausgeführt wird. Um physikalische Signale mit digitaler Technik zu erfassen und zu bearbeiten,
müssen die Signale abgetastet bzw. zeitdiskretisiert werden, d. h. die Werte werden nur zu bestimmten Zeitpunkten erfasst und bearbeitet. Außerdem können die erfassten Messwerte nur
mit endlicher Genauigkeit gespeichert werden, so dass bei der Digitalisierung eine Wertdiskretisierung stattfindet. Die Probleme, die beim Übergang von analoger zu digitaler Signaltechnik
auftreten, werden in diesem Versuch behandelt.
In dem Experiment wird eine Soundkarte als Analog/Digital-Wandler benutzt. Zeitlich variierende analoge Signale werden von einem Frequenzgenerator erzeugt und mit der Soundkarte
digitalisiert. Dabei wird der Einfluss verschiedener Effekte auf das digitalisierte Signal untersucht. Als reale zeitlich variierende Signale werden Töne einer Stimmgabel, eines Tongebers für
das Tonwahlverfahren sowie die menschliche Stimme aufgenommen und analysiert.
Kenntnisse
• Analog-Digital-Wandler, Digital-Analog-Wandler, Sample & Hold
• Theoretische Beschreibung von Signalen
• Fouriertransformation, diskrete Fouriertransformation
• Abtastung, Abtasttheorem
• Aliasing-Effekt, Leakage-Effekt
• Tiefpassfilter
Literatur
[1] Stearns: Digitale Verarbeitung analoger Signale, Oldenbourg
Kapitel 3: Überblick über kontinuierliche Transformationen, Übertragungsfunktionen . . .
Kapitel 4: Das Abtasten und Messen von Signalen
Kapitel 5: Die diskrete Fouriertransformation
Kapitel 7: Spektrale Berechnung bei abgetasteten Signalen
[2] M. Meyer: Signalverarbeitung, Vieweg, 2000
Kapitel 5: Digitale Signale
[3] Ohm, Lüke: Signalübertragung, Springer-Verlag, 2002
Kapitel 3: Diskrete Signale und Systeme
[4] Hering, Bressler, Gutekunst: Elektronik für Ingenieure, Springer, 2001
Kapitel 9: Digital-Analog- und Analog-Digital-Wandler
1
1
Grundlagen
1.1
Vorkenntnisse
In diesem Abschnitt werden Grundlagen zusammengefasst, die zum Verständnis der nachfolgenden Theorie unbedingt erforderlich sind.
1.1.1
Die Fourier-Transformation
1.1.1.1 Die Fourier-Integraltransformation (FIT) Die Theorie der linearen Signalverarbeitung lässt sich auf harmonische Funktionen gründen. Diese sind Eigenfunktionen der LTISysteme (Linear Time Invariant Systems) und können, da sie eine vollständige orthonormale
Basis des Raumes der quadratintegrablen Funktionen bilden, als Grundlage für entsprechende
Betrachtungen dienen. Das Verhalten komplizierter Zeitfunktionen g(t) lässt sich also studieren,
wenn man deren Frequenzanteile G(f) kennt. Die FIT leistet genau diesen Basiswechsel vom
Zeit- in den Frequenzraum: sie stellt eine Funktion über der Basis der harmonischen Funktionen
dar. Die Umkehrtransformation macht dies rückgängig.
Die Fourier-Transformation (FT) und die inverse Fourier-Transformation sind wie folgt definiert:
1
FT: F (ω) = √
2π
Z∞
f (t)e
−iωt
dt
FT
−1
:
Z∞
1
f (t) = √
2π
−∞
F (ω)eiωt dω
(1)
−∞
Weitere wichtige Eigenschaften sind:
f (t) periodisch
f (t) diskret
∗
f (t) reell ⇔ F (ω) = F (−ω)
⇔ F (ω) diskret
(2)
⇒ |F (ω)| gerade
(4)
⇔ F (ω) periodisch
(3)
1.1.1.2 Die Faltung Im Folgenden werden wir gelegentlich in die Situation kommen, dass
wir zwei Signale, deren Spektren wir kennen, miteinander multiplizieren. Das Spektrum des
Produktes kann dann leicht über die Faltung bestimmt werden. Der Faltungssatz besagt:
FT [f (t) · g(t)] = F (ω) ∗ G(ω)
FT [F (ω) · G(ω)] = f (t) ∗ g(t) .
(5)
Eine Multiplikation im Zeitraum geht also in eine Faltung im Frequenzraum über. Die Faltung
ist durch folgendes Integral definiert:
[f (τ ) ∗ g(τ )] (t) =
Z∞
f (τ ) g(t − τ ) dτ .
(6)
−∞
Das Ergebnis einer Faltung ist also eine Funktion mit dem Argument t. Anschaulich bedeutet
die Faltung, dass die Funktion g an der y-Achse gespiegelt wird, um das Argument t der Faltung
entlang der x-Achse verschoben wird und dann die Korrelation der beiden Funktionen berechnet
wird.
1.1.1.3 Die Fourier-Reihe Gleichung 2 besagt, dass das Spektrum einer periodischen Funktion nur aus diskreten Werten besteht. Diese Eigenschaft macht sich die Fourier-Reihenentwicklung
zu Nutze, um eine Funktion mit der Periodenlänge T zu transformieren.
2
cm
1
=
T
ZT
2π
f (t) e−i T
mt
dt
f (t) =
∞
X
2π
cm ei T
mt
(7)
m=−∞
0
1.1.1.4 Die diskrete Fourier-Transformation Sollen digitalisierte Zeitreihen transformiert
werden, so benötigt man die diskrete Fourier-Transformation (DFT). Sie transformiert einen
Vektor aus N Werten xn in einen neuen Vektor aus N Werten cm . Die diskrete FourierTransformation kann aus der Fourier-Reihe abgeleitet werden, indem das Integral durch eine
Riemann’sche Summe ersetzt wird.
cm
N −1
2π
1 X
=
xn e−i N mn
N n=0
xn =
N
−1
X
2π
cm ei N mn
(8)
m=0
Dabei kann der Faktor 1/N nach belieben auch in die Definition von xn verschoben werden.
Die DFT erbt von der Fourier-Reihe die Eigenschaft, dass das zu transformierende Zeitintervall
als periodisch fortgesetzt interpretiert wird. Dieser Umstand wird bei der Anwendung der DFT
noch eine Rolle spielen.
1.1.2
Die dB-Skala
In der Signalverarbeitung interessiert man sich häufig für das Verhältnis zweier Signalleistungen
P/P0 . Das kann z. B. die Leistungsverstärkung eines Verstärkers oder die Dämpfung einer Übertragungsstrecke sein. Hat man eine Kette von z. B. Übertragungsstrecken und Verstärkern, so
müssen die Verstärkungen und Dämpfungen der einzelnen Glieder miteinander multipliziert werden, um die Gesamtdämpfung zu erhalten. Es ist daher praktisch, diese Leistungsverhältnisse
logarithmisch anzugeben, da eine Übertragungskette dann durch die Summe der Verstärkungen/Dämpfungen ihrer Bestandteile beschrieben werden kann. Außerdem hat eine logarithmische Einheit den Vorteil, einen sehr großen Wertebereich mit einfach zu handhabenden Zahlen
abdecken zu können. Daher wird der Leistungspegel“ mit der Einheit 1 Bel definiert:
”
LP (Bel) = log10
P
P0
LP (dB) = 10 log 10
P
U
= 20 log 10
P0
U0
(9)
Um die Zahlenwerte noch schöner“ zu machen, wird in der Praxis der zehnte Teil, also das
”
dezi-Bel“ (dB) benutzt. Da man üblicherweise Amplituden, z. B. Spannungen misst, wird der
”
quadratische Zusammenhang zwischen Leistung und Amplitude vor den Logarithmus gezogen.
1.2
Digitale Signale
Ein analoges Signal kann dargestellt werden als eine Funktion der Zeit mit reellem Wertebereich:
s(t) ∈ R. Soll eine solche Funktion in einem Rechner dargestellt werden, ergeben sich zwei
Probleme. Zum einen stehen in einem Rechner einzelne Speicherplätze zur Verfügung, so dass
aus der Funktion eine Folge von Zahlen werden muss. Zum anderen hat jeder der Speicherplätze
nur eine endliche Genauigkeit, so dass der Wertebereich diskret sein muss. Aus dem analogen
Signal muss also eine Zahlenfolge mit diskretem Wertebereich werden: st ∈ Z. Im Folgenden soll
geklärt werden, welche Konsequenzen diese Einschränkungen haben.
1.2.1
Wertdiskretisierung
Die Wertdiskretisierung ist eine Rundung des analogen, reellen Wertes auf eine ganze Zahl.
Die Abweichung des digitalisierten Wertes vom Analogen wird Quantisierungsfehler“ genannt
”
3
und liegt im Intervall [− 12 ; 12 ]. Wenn die Diskretisierung der einzelnen Werte fein genug ist,
dann ist bei der Digitalisierung einer Zeitreihe von Werten die Folge von Quantisierungsfehlern
stochastisch verteilt und enthält keine Informationen über das Signal mehr. Daher kann das
Fehlersignal, das dem Originalsignal überlagert werden muss, um das quantisierte Signal zu
erhalten, als Rauschen aufgefasst werden.
Um das Rauschen im Verhältnis zum eigentlichen Signal zu quantisieren, wird das Signal”
Rausch-Verhältnis“ (SNR, Signal-Noise-Ratio) eingeführt.
SNR(dB) = 20 log10
SA
2N /2
= 20 log 10
= 20 · N · log10 2 ≈ 6 · N
NA
1/2
(10)
Dabei ist SA die Signalamplitude und NA die Rauschamplitude. Wenn man, wie in der Praxis
üblich, annimmt, dass die Werte im Dualsystem mit N Stellen gespeichert werden, so ist die maximale Signalamplitude 2N /2, da positive und negative Halbwellen in den Wertebereich passen
müssen.
1.2.2
Zeitdiskretisierung
Wird ein zeitkontinuierliches Signal erfasst, indem sein Wert periodisch mit der Abtastfrequenz
fs (Samplingfrequenz) gemessen wird, so ist sofort offensichtlich, dass es eine maximale Signalfrequenz gibt, die erfasst werden kann. Man stelle sich ein Signal mit nur einer Frequenzkomponente
z. B. ein Sinussignal vor. Dieses muss mindestens in jedem Minimum und in jedem Maximum
erfasst werden, sonst ist die Signalfrequenz im zeitdiskretisierten Signal nicht mehr erkennbar.
Folglich findet durch die Zeitdiskretisierung eine Bandbreitenbegrenzung des erfassten Signals
statt. Die maximal erfassbare Signalfrequenz wird Nyquist-Frequenz“ genannt und beträgt
”
fN = fs /2.
s(t)
sd (t)
E
(t)
t
t
S(f)
t
Sd (f)
E
(f)
fs
f
fs
f
fs
f
Abbildung 1: Oben: Diskretisierung der Werte im Zeitraum. Unten: Periodisierung des Spektrums.
E
E
E
E
E
Es soll nun erläutert werden, wie ein digitalisiertes Signal wieder analog ausgegeben werden
kann. Dazu werden alle Signale auch im Frequenzraum betrachtet. In Abb. 1 ist eine analoges
Signal s(t) mit dem dazugehörigen Leistungsspektrum S(f ) dargestellt (durchgezogene Linie).
Die Abtastung des Signals entspricht einer Multiplikation mit einer Folge äquidistanter δ-Pulse,
die -Funktion genannt wird ( – kyrillischer Buchstabe Scha“). Das Leistungsspektrum der
”
-Funktion ist wieder eine
-Funktion, wobei der Abstand der δ-Pulse jetzt der Abtastfrequenz fs entspricht. Um das Spektrum Sd (f ) der Abtastwerte sd (t) zu erhalten, werden gemäß
dem Faltungssatz aus Gleichung 5 das Signalspektrum S(f ) und das Spektrum der Abtastfunktion
(f ) miteinander gefaltet. Das Ergebnis ist in Abb. 1 zu sehen (Durchgezogene Linie).
Das ursprüngliche Signalspektrum ist im Abstand fs periodische fortgesetzt worden. Soll also
ein digitalisierte Signal wieder analog ausgegeben werden, so müssen die neu hinzugekommenen
Frequenzen herausgefiltert werden. Das geschieht mit einem Tiefpass-Filter mit der Grenzfrequenz fg = fN = fs /2.
4
Es ergibt sich nun ein Problem, wenn das ursprüngliche analoge Signal Frequenzen enthält, die
oberhalb der Nyquist-Frequenz fN liegen. Das Spektrum eines solchen Signals ist in Abb. 1
in S(f ) gestrichelt eingezeichnet. Betrachtet man dessen periodisiertes Spektrum Sd (f ) so erkennt man, dass die periodisch wiederholten Spektren überlappen. Im Bereich des gültigen,
bandbreitenbegrenzten Spektrums [0; fN ] kommen dadurch auch die Frequenzen zu liegen, die
eigentlich außerhalb dieses Bereiches liegen sollten. Die bei einer Abtastung mit fs nicht erfassbaren Frequenzen größer fN = fs /2 tauchen also an falscher Stelle wieder auf. Dieser Effekt
wird Aliasing-Effekt“ genannt. Um ihn zu verhindern muss schon das analoge Signal bandbrei”
tenbegrenzt sein. Auch das kann mit einem Tiefpass-Filter geschehen.
1.3
1.3.1
Technische Realisierung
Analog-Digital-Wandler
Damit Signale in digitaler Form verarbeitet werden können, müssen die analogen Eingangssignale erst in eine digitale Form gebracht werden. Hierzu benutzt man Analog-Digital-Wandler,
die nach verschiedenen Prinzipien arbeiten können (Parallelverfahren, Zählverfahren, Wägeverfahren, . . . ). Die verwendeten Verfahren unterscheiden sich in der Genauigkeit und Schnelligkeit.
Hier soll kurz auf zwei Verfahren eingegangen werden.
1.3.1.1 Das Zählverfahren Abbildung 2 (links) zeigt den schematischen Aufbau eines A/DWandlers, der nach dem Sägezahn- oder Single-Slope-Verfahren arbeitet. Der Wandlungsvorgang
wird mit einem Impuls am Eingang Start“ ausgelöst. Dadurch wird der Binärzähler auf Null
”
gesetzt und der Sägezahngenerator beginnt, eine Spannungsrampe zu erzeugen. Die Ausgangsspannung des Sägezahngenerators wird mit der Eingangsspannung verglichen. Solange die Eingangsspannung Ue größer als die Ausgangsspannung des Sägezahngenerators ist, ist der Ausgang
des Komparators auf logisch 0. Der Zähler ist also am Eingang (EN, enable) aktiviert und zählt
die Taktimpulse. Sobald die Sägezahnspannung die Eingangsspannung Ue übersteigt, schaltet
der Komparator seinen Ausgang auf logisch 1. Dadurch wird der Zähler angehalten und der
Ausgang Fertig“ signalisiert der nachfolgenden Elektronik, üblicherweise ein Mikroprozessor,
”
dass der Wandlungsvorgang abgeschlossen ist. Der digitalisierte Wert kann vom Ausgang gelesen
werden.
1.3.1.2 Das Wägeverfahren Abbildung 2 (rechts) zeigt das Blockschaltbild eines A/D-Wandlers, der die digitalen Werte nach dem Prinzip der sukzessiven Approximation ermittelt. Der
Wandlungsvorgang wird durch einen Impuls am Eingang Start“ ausgelöst. Dadurch wird der
”
Digitalwert auf null gesetzt. Über den D/A-Wandler wird stets die dem Zahlenwert entsprechende Spannung auf den invertierenden Eingang des Komparators gegeben. Dann werden, beginnend
beim höchstwertigen Bit (MSB, most significant bit), folgende Schritte durchlaufen: Das betreffende Bit wird auf 1 gesetzt. Der Komparator zeigt nun an, ob die Eingangsspannung Ue größer
(Ausgang auf 1) oder kleiner (Ausgang auf 0) als die dem Zahlenwert entsprechende Spannung
Fertig
Ue
EN
Takt
Reset
Start
Takt
Zähler
Sägezahn−Generator
Fertig
grösser/
kleiner
Ue
Steuerlogik
Ausgang
Ausgang
D/A−Wandler
Reset
Start
Abbildung 2: Blockschaltbilder von A/D-Wandlern. Links: Single-Slope Verfahren, rechts: A/DWandler nach dem Prinzip der sukzessiven Approximation
5
ist. Sollte die Eingangsspannung kleiner sein, der Digitalwert also zu groß sein, dann wird das
soeben gesetzte Bit wieder gelöscht. Dann wird mit dem nächst kleineren Bit genau so verfahren,
bis alle Bits bestimmt sind. Die Geschwindigkeit, mit der die Bits bestimmt werden, wird vom
Signal am Eingang Takt“ bestimmt. Das Ende des Wandlungsvorgangs wird der nachfolgenden
”
Elektronik über ein Signal am Ausgang Fertig“ mitgeteilt, und der digitalisierte Wert kann
”
ausgelesen werden.
1.3.2
Sample & Hold-Schaltung
Für viele A/D-Wandler ist es notwendig, dass die analoge Eingangsspannung während des Wandlungsvorgangs konstant bleibt. Die beiden oben vorgestellten A/D-Wandler gehören dazu. Diese
Aufgabe wird von der Sample & Hold“ Schaltung übernommen, die in Abb. 3 dargestellt ist.
”
Herzstück dieser Schaltung ist ein Kondensator, der über einen Schalter mit der Eingangsspannung verbunden werden kann. Die Spannung über dem Kondensator wird mit einem als
Impedanzwandler geschalteten Operationsverstärker (OP) gepuffert.
Zu Beginn eines Digitalisierungsvorgangs wird der Schalter für eine kurze Zeit geschlossen.
Währenddessen wird der Kondensator vom linken OP ge- oder entladen, so dass die Spannung über dem Kondensator, also die Spannung am Ausgang, der Eingangsspannung entspricht.
Sobald der Schalter geöffnet ist, steht die Spannung am Kondensator unverändert am Ausgang
zur Verfügung.
Der rechte OP ist nötig, um einen Strom am Ausgang der Schaltung zu liefern ohne den Kondensator zu entladen. Der linke OP wird gebraucht, um einen hohen Ladestrom für den Kondensator
zur Verfügung zu stellen, um ihn in kurzer Zeit laden zu können. Der Schalter ist in der Praxis aus ein oder mehreren Transistoren aufgebaut und wird über die Leitung ein“ elektronisch
”
gesteuert.
1.3.3
Digital-Analog-Wandler
Ein einfacher Digital-Analog- (DA) Wandler ist in Abb. 3 dargestellt. DA-Wandler erhalten am
Eingang eine binär kodierte Zahl (Digitalwort). Eine konstante Referenzspannung speist über
digital gesteuerte Schalter und binär gestufte Widerstände Strom in den Knoten eines addierenden Operationsverstärkers ein. Der vom Netzwerk in den Knoten fließende Strom ist dem
Produkt aus der Referenzspannung und der angelegten Digitalzahl proportional. Der Operationsverstärker stellt die Ausgangsspannung so ein, dass der Strom durch den Rückführwiderstand
RS den Strom aus dem Netzwerk genau kompensiert. Die Ausgangsspannung ist dem angelegten
Digitalwort proportional, ihre Polarität ist der Referenzspannung entgegengesetzt.
1.3.4
Tiefpassfilter
Die Aufgabe eines Tiefpass-Filters ist es, alle Frequenzen, die kleiner als eine festgelegte Grenzfrequenz fg sind, ungehindert vom Eingang zum Ausgang passieren zu lassen und Frequenzen
1
2
4
8
16
32
Uref
RS
Uout
32R
Uin
16R
8R
4R
2R
R
Ua
C
ein
Abbildung 3: Links: Schaltbild eines Abtast-Halte-Gliedes, rechts: Schaltbild eines D/A-Wandlers
6
größer fg vollständig zu unterdrücken. Die Übertragungsfunktion eines idealen Tiefpassfiters ist
im Frequenzraum also eine Stufenfunktion bei fg . Aus kausalen Gründen ist es allerdings nicht
möglich, einen idealen Tiefpass zu bauen (Man überlege sich wie ein teifpassgefilterter δ-Impuls
aussieht.). Daher haben reale Tiefpassfilter eine Übertragungsfunktion, die für kleine Frequenzen
etwa Eins ist und für große Frequenzen allmählich gegen Null geht. Die Flanke dieser Übertragungsfunktion ist je nach Qualität des Filters unterschiedlich steil und der Durchlassbereich
mehr oder weniger wellig. Die Grenzfrequenz eines Filters wird definiert als die Frequenz, bei
der die Leistung des Ausgangssignals auf die Hälfte des Durchlassbereiches abgefallen ist. Das
entspricht einer Dämpfung von 3 dB.
1.4
Eine Anwendung: Spektralanalyse
Die Bestimmung des Leistungsspektrums eines Signals auf analogem Wege ist keine triviale
Aufgabe (Der geneigte Leser überlege sich, wie so etwas geht.). Wenn ein Signal jedoch einmal
digitalisiert ist, so ist es ein leichtes, das Spektrum auszurechnen. Im einfachsten Falle braucht
man nur die Koeffizienten der DFT aus Gleichung 8 auszurechnen. Dabei ist jedoch zu beachten,
dass die DFT von der Fourier-Reihe abstammt und daher voraussetzt, dass der zu transformierende Zeitabschnitt periodisch fortgesetzt wird. Wird von einem unbekannten Signal aber ein
beliebiger Ausschnitt digitalisiert, so ist nicht damit zu rechnen, dass die periodische Fortsetzung
auch dem originalen Signal entspricht.
In Abb. 4 sind links oben als durchgezogene Linie ein analoges Signal und mit • die zugehörigen
Abtastwerte in einem 32 Werte langen Puffer dargestellt. Es passen etwas mehr als drei Schwinxn
xn
n
32
n
32
cm
−16
xn
cm
16
m
−16
n
32
cm
16
m
−16
16
m
Abbildung 4: Links: Abgetastetes Signal und dessen DFT, Mitte: diskretisiertes Hanning-Fenster mit
diskretem Spektrum, rechts: Mit Hanning-Fenster multipliziertes Signal und diskretes Spektrum. Das
Zeitfenster ist 32 Werte lang (von 0 bis 31), ◦ gehören zur periodischen Fortsetzung. In den Spektren
sind rein reelle Werte mit ◦ gekennzeichnet.
gungen in den Puffer. Die mit ◦ außerhalb des Puffers dargestellten Werte zeigen die periodische
Fortsetzung des Signals, die dem gestricheltem Analogsignal entsprechen. Im zugehörigen Spektrum darunter sind zwei δ-Pulse eingezeichnet, die das Spektrum des Analogsignals darstellen.
Das Ergebnis der DFT, die ein diskretes Spektrum liefert, ist mit • und ◦ dargestellt. • bezeichnet den Betrag eines komplexen Fourier-Koeffizienten, ◦ stellt rein reelle Werte dar. Die Werte
des Spektrums sind in den Kanälen drei und vier, zwischen denen die Frequenz des analogen
Signals liegt, am größten. Aber auch alle anderen Werte des Spektrums sind von Null verschieden. Dieses Breitlaufen der Pulse wird als Leakage-Effekt“ bezeichnet und kommt daher, dass
”
die periodischen Fortsetzungen des Signals nicht zusammenpassen.
Um dem Leakage-Effekt entgegenzuwirken, können die Abtastwerte mit einer Fensterfunktion
multipliziert werden, die das Signal an den Fensterrändern stetig auf Null abfallen lässt. Eine
solche Fensterfunktion ist in Abb. 4 oben in der Mitte zu sehen. Es gibt eine Vielzahl von
Fensterfunktionen; in den meisten Fällen ist allerdings das Hanning-Fenster“mit den Werten
”
7
1 1
xn = − cos
2 2
2π
n
N
(11)
günstig. Das Spektrum des Hanning-Fensters hat also in den Frequenzkanälen Null und Eins
einen von Null verschiedenen Wert. Damit hat es das schmalste in der DFT mögliche Spektrum
überhaupt.
Rechts in der Abb. 4 sind die schon zuvor gezeigten Messdaten nach der Multiplikation mit dem
Hanning-Fenster zu sehen. Die periodische Fortsetzung des Fensters verläuft glatt, da die Werte
durch die Bearbeitung an dieser Stelle stetig und differenzierbar Null werden. Das in der DFT
ermittelte Spektrum des bearbeiteten Signals ergibt sich aus der Faltung des Spektrums des
Hanning-Fensters mit dem des analogen Signals. Die Kanäle drei und vier haben die größten
Werte, und durch die Faltung mit dem Hanning-Spektrum erhalten auch die benachbarte Kanäle,
also zwei und fünf, von Null verschiedene Werte. Alle anderen Kanäle sind Null. Im allgemeinen
Fall eines Signals mit beliebiger Frequenz ist die DFT der mit dem Hanning-Fenster bewerteten
Messdaten die beste Annäherung an den tatsächlichen δ-Puls im Frequenzraum.
2
Geräte und Zubehör
• Computer mit Soundkarte und Labview, Software
• Frequenzgeneratoren (HP und Wavetek)
• Mikrophon mit Vorverstärker
• Stimmgabel (nur am Körper anzuschlagen)
• Tongeber für das Tonwahlverfahren
• Multipliziereinheit mit Spannungsversorgung
3
Aufgaben & Hinweise
3.1
Qualität des A/D-Wandlers
Der Eingang der Soundkarte wird auf 0 V gelegt. Es werden 5120 Messwerte mit voller Auflösung
(16 Bit) aufgenommen und gespeichert.
• Wie groß ist das Rauschen der Soundkarte? Wieviel Bit des Messwertes sind wirklich
brauchbar? Es wird ab jetzt immer mit der ermittelten Auflösung gemessen.
• Wie groß ist der Durchschnitt der Werte? Welche Bedeutung hat das in der (Audio-)Praxis?
3.2
Qualität des Tiefpassfilters
Bei einer Abtastfrequenz von 44,1 kHz wird der Frequenzgang der Soundkarte bestimmt. Unter
100 Hz wird in 10 Hz Schritten gemessen, bis 1000 Hz in 100 Hz Schritten, und dann bis zum
Verschwinden des Signals im Rauschen in 1000 Hz Schritten. Die kleinste vermessene Frequenz
muss ein Minimum und ein Maximum im Puffer haben. Als Signalamplitude kann die Peak-toPeak Amplitude des Signals festgehalten werden.
• In einem Diagramm werden die Signalamplituden in dB aufgetragen. Bezugsgröße ist die
Amplitude bei 1 kHz. Die Frequenzachse ist logarithmisch.
• Es wird die obere Grenzfrequenz der Soundkarte bestimmt.
8
3.3
Aliasing-Effekt
Zur Demonstration des Aliasing-Effektes wird bei einer Abtastfrequenz von 8 kHz ein Sinussignal
mit 3 kHz und eines mit 5 kHz aufgenommen und gespeichert. Es kann unter Umständen nötig
sein, die Eingangsverstärkung (IGain) zu erhöhen.
• Es werden von beiden Signalen 10 ms dargestellt.
• Die ungefähren Frequenzen der Signale werden bestimmt, indem die Anzahl der Maxima
gezählt wird. Die erhaltenen Werte werden mit den tatsächlichen Werten verglichen.
3.4
Spektralanalyse – Leakage-Effekt
Man wähle eine von der Soundkarte unterstützte Abtastrate (8 kHz, 11025 Hz, 22050 Hz,
44100 Hz). Man wähle eine natürliche Zahl n ∈ [50; 100].
• Es wird am Funktionsgenerator eine Frequenz f1 eingestellt, bei der genau n Schwingungen
in den Puffer passen. Es werden die Spektren mit und ohne Hanning-Fenster berechnet
und gespeichert.
• Es wird am Funktionsgenerator eine Frequenz f2 eingestellt, bei der n + 12 Schwingungen
in den Puffer passen. Es werden die Spektren mit und ohne Hanning-Fenster berechnet
und gespeichert.
• Die Auswirkung des Hanning-Fensters auf beide Spektren wird im Protokoll diskutiert.
3.5
Analyse realer Signale
Im Folgenden wird mit einer Abtastrate von 8 KHz gearbeitet. Zur Aufnahme der Spektren wird
das Hanning-Fenster verwendet.
• Es werden die Frequenzen zweier Stimmgabeln bestimmt.
• Wie werden die Ziffern und Zeichen beim Tonwahlverfahren in Töne kodiert?
• Es werden Wellenform und Spektrum eines Dreieck- oder Rechtecksignals aufgenommen.
Im Protokoll werden die gemessenen Amplituden mit den erwarteten verglichen.Welchen
Einfluss hat der Tiefpassfilter im Zeit- und Frequenzraum?
3.5.1
Vokale
Zu Erzeugung eines Vokals erzeugen die Stimmbänder einen Frequenzkamm, bestehend aus
einer Grundfrequenz und vielen Oberwellen. Der Rachenraum bildet einen Resonanzkörper, der
verschiedene Frequenzen hervorhebt und dämpft und so dem Frequenzkamm der Stimmbänder
eine Einhüllende verleiht.
• Es werden von allen Teilnehmern die Vokale a“ und i“ aufgenommen und im Frequenz”
”
raum dargestellt, gespeichert und im Protokoll abgebildet.
• Welche Gemeinsamkeiten haben gleiche Vokale bei verschiedenen Sprechern?
• Es wird die Grundfrequenz von jedem Sprecher bestimmt.
9
3.5.2
Amplitudenmodulation
In der Radio- und Fernsehtechnik wird einer hochfrequenten Trägerwelle (z. B. 720 kHz, WDR 2
auf MW) ein Signal (z. B. Audio, 0–5 kHz) aufgeprägt, indem es die Amplitude des Trägers
verändert (Amplitudenmodulation, AM). Die Amplitudenmodulation ist eine Multiplikation des
Trägers mit dem Signal, das evtl. mit einem Gleichanteil überlagert wird.
Um eine AM durchzuführen, wird an einem Funktionsgenerator eine Trägerwelle von etwa 2 kHz
eingestellt. Der zweite Generator erzeugt eine Signalwelle von 100 Hz. Beide Signale werden der
Multipliziereinheit zugeführt.
• Das AM-Signal wird im Zeit- und im Frequenzraum dargestellt.
• Welche Frequenzen werden im AM-Signal erwartet und warum? Welche Frequenzen enthält
das AM-Signal tatsächlich? Wie können eventuelle Abweichungen erklärt werden?
4
Fragen zur Vorbereitung
• Wie sieht die Fouriertransformierte einer Sinus- und einer Cosinus-Funktion aus? Wie
sehen die Fourier-Reihen von Dreieck- und Rechteckfunktionen aus?
• Welche Bedeutung haben Real- und Imaginärteil (bzw. Betrag und Phase) der FourierTransformierten einer reellen Funktion?
• Welche Informationen stecken in den negativen Frequenzen, wenn die Zeitfunktion reell
ist?
• Wie sieht die Faltung einer Funktion f (t) mit der Delta-Funktion δ(t) aus? Wie sieht die
Faltung mit der verschobenen Delta-Funktion δ(t − τ ) aus?
• Wie ändern sich Pegelangaben in dB, wenn die Bezugsleistung P0 geändert wird? Wie
ändern sich die Pegelwerte, wenn die Leistung P mit einem konstanten Faktor multipliziert
wird?
• Welche Größen werden diskretisiert“, wenn ein analoges Signal in ein digitales übergeht?
”
• Wie lässt sich die Abweichung der quantisierten Größe von ihrem analogen Ausgangswert
charakterisieren?
• Wann wird die Abtastung kritisch? Was kann man dagegen tun? Was sind typische Abtastraten in der Praxis?
• Was versteht man unter Aliasing-Effekt?
• Erläutern Sie zwei Verfahren, um analoge Spannungswerte zu digitalisieren.
• Wie ist der zeitliche Verlauf der Ausgangssignale bei den verschiedenen Wandlungsverfahren?
• Was passiert, wenn sich das Eingangssignal während des Wandlungsvorgangs ändert?
• Was sind die Vor- und Nachteile der einzelnen Verfahren?
• Was sind typische Wandlungstiefen für A/D-Wandler in der Praxis? Was sind typische
Abtastfrequenzen?
• Was ist die Ursache für den Leakage-Effekt?
• Wie sieht das DFT-Spektrum eines Sinussignals aus, von dem genau 7 Wellen in den
Messspeicher passen? Wie sieht die DFT aus, wenn das Signal zuvor mit dem HanningFenster bewertet wird?
• Wie sehen die Spektren von periodischen aber nicht sinusförmigen Signalen aus? Welche
Ähnlichkeit haben sie mit den Spektren gesprochener Vokale?
10