6.1 Weltbilder 6.1.3 Das heliozentrische Weltbild (heliocéntrico del

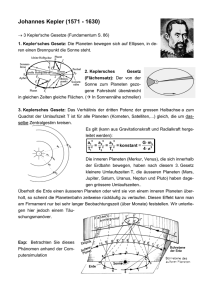
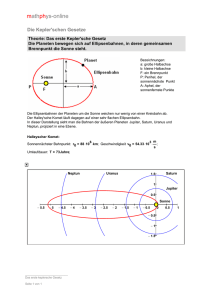
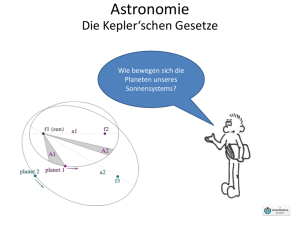
6 Gravitation
© Hofer
6
Gravitation (gravitación, la)
A1:
Informiere dich über unser Sonnensystem und trage dein Wissen in Form eines
Kurzreferates vor.
6.1
Weltbilder
1
6.1.2 Das geozentrische Weltbild(concepto (el) geocéntrico del mundo)
•
Aristoteles (384 – 322 v. Chr.)
Er sagte, dass die Erde eine Kugel sei und dass sich die Planeten
mit konstanter Geschwindigkeit auf Kreisbahnen um die Erde bewegen.
Die Erde ruht im Zentrum des Weltraums.
•
Ptolemaios (87-165)
Er verbesserte das geozentrische Weltbild in seinem Werk „Almagest“.
Ptolemaios beschrieb ein System in dem sich alle Himmelskörper nach
geometrischen Prinzipien bewegen sollten.
Dadurch konnte man die Planetenpositionen vorausberechen, was für die Seefahrt
und die Zeitrechnung sehr wichtig war.
Von der christlichen Kirche wurde das Weltbild als das einzig gültige angesehen.
6.1.3 Das heliozentrische Weltbild (heliocéntrico del mundo concepto )
•
Herakleides von Pontos (ca. 388 – 310 v. Chr.) und Aristarch von Samos (310230 v. Chr.)
Sie entwickelten ein heliozentrisches Weltbild. Alle Himmelskörper sollten sich
auf Kreisbahnen um die Sonne bewegen. Diese Idee setzte sich in der Antike aber
nicht durch.
•
Nikolaus Kopernikus (1473-1543)
1543 veröffentlichte er ein Buch mit dem Titel „De revolutionibus orbium
coelestium“. Er beschrieb darin das heliozentrische Weltbild:
1.
2.
3.
4.
5.
6.
7.
Die Sonne steht im Mittelpunkt der Welt.
Die Sterne ruhen im Raum.
Die Erde ist ein Planet und läuft in einer Kreisbahn in einem Jahr um
die Sonne. Sie dreht sich dabei von Westen nach Osten täglich einmal
um ihre Achse.
Der Mond läuft in einer Kreisbahn um die Erde.
Die Planeten bewegen sich in Kreisbahnen um die Sonne.
Die Erdbahnebene heißt Ekliptik.
Die Erdbahnachse bildet mit der Ekliptik-Normalen einen Winkel von
23,5°.
6 Gravitation
© Hofer
2
Abb.1: Bewegung der Erde um die Sonne
Abb.2: Rückläufige Marsbewegung
A2:Erkläre die Rückläufige
Marsbewegung!
6 Gravitation
•
© Hofer
3
Johannes Kepler(1571-1630)
Als Kepler seine ersten zwei Kepler´schen Gesetze aufstellte lehrte er in Prag.
Er bediente sich dort, der für diese Zeit ausgezeichneten Messdaten von Tycho Brahe.
Besonders genau hatte Tycho Brahe die Marsbahn vermessen. Kepler machte sich an
die Aufarbeitung dieser Daten.
Kepler tat nun einen ungeheuer kühnen und bedeutungsvollen Schritt:
Er gab die aristotelische Vorstellung von der gleichförmigen Kreisbewegung auf.
Kepler verwendet zur Beschreibung der Planetenbahnen Ellipsen.
1609 veröffentlichte er das Buch „Astronomia nova“
Darin enthalten waren die ersten zwei Kepler Gesetze:
1.Kepler´sches Gesetz
Die Planeten bewegen sich auf Ellipsen, in deren gemeinsamem Brennpunkt die
Sonne steht.
Abb.1: 1.Kepler´sches Gesetz
2.Kepler´sches Gesetz
Der von der Sonne zum Planeten gezogene Radiusvektor überstreicht in gleichen
Zeiten gleiche Flächen.
Abb.2: 2.Kepler´sches Gesetz
6 Gravitation
© Hofer
2. Kepler Gesetz (Java Applet)
A1: Leite das 2.Kepler´sches Gesetz mithilfe des Drehimpulserhaltungssatzes her!
Zehn Jahre später veröffentlichte er das Buch „Harmonices mundi“.
Darin enthalten war das dritte Kepler Gesetz.
3.Kepler´sches Gesetz
Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben
der großen Bahnhalbachsen.
T12 a13
=
T22 a 32
Abb.3: 3.Kepler´sches Gesetz
A2:
Leite das 3.Kepler´sches Gesetz her!
A3:
Verwende zur Erklärung und zur Veranschaulichung der Kepler Gesetze
das entsprechende Java Applet!
4
6 Gravitation
6.2
© Hofer
Gravitation (gravitación, la)
6.2.1 Das Gravitationsgesetz (ley (la) de la gravitación o de Newton)
Isaac Newton (1642 – 1727) veröffentlichte 1687 in der „Philosophiae naturalis
principia mathematica“ seine Erkenntnisse über die Natur.
Darunter war auch das Gravitationsgesetz:
Newton´sches Gravitationsgesetz
Zwei Körper mit den Massen M und m ziehen einander im Abstand r mit der
Gravitationskraft F an:
F=G
M.m
r2
F…Betrag der Gravitationskraft
G…Gravitationskonstante
M…Masse des ersten Körpers
m…Masse des zweiten Körpers
r…Abstand zwischen den beiden Körpern
G = 6,7.10-11 m3.kg-1.s-2
Die Gravitationskonstante wurde von Cavendish (1731-1810) experimentell bestimmt.
A1: Zeige, dass die Einheit der Gravitationskonstante richtig ist!
A2: Schreibe das Gravitationsgesetz vektoriell und begründe deine Überlegungen!
A3: Berechne die Fallbeschleunigung g!
A4: Trage die Fallbeschleunigung in Abhängigkeit der Entfernung zum Erdmittelpunkt
in ein Diagramm ein!
A5: Berechne die Anziehungskraft auf einen Satelliten (m=1200kg) der in der Höhe
von 1000km um die Erde kreist.
Mit welcher Geschwindigkeit bewegt sich der Satellit?
5
6 Gravitation
© Hofer
6
6.2.2 Die Erforschung der Planeten
•
Bestimmung der Sonnenmasse
Die Erde bewegt sich als „Satellit“ annähernd auf einer Kreisbahn um die Sonne. Aus dem
3. Kepler Gesetz folgt:
T 2 4π 2
=
r 3 GM
T…Umlaufzeit des Satelliten
r…Bahnradius des Satelliten
G…Gravitationskonstante
M…Zentralmasse
A1: Bestimme die Masse der Sonne aus den dir bekannten Daten.
•
Die Bestimmung der Bahnradien der Planeten
Das 3. Kepler Gesetz ermöglicht die Bestimmung der Bahnradien aus den Umlaufzeiten
der Planeten, wenn die Sonnenmasse bekannt ist oder wenn ein Bahnradius eines Planeten
genau bekannt ist.
A3: Bestimme den Bahnradius des Mars! (T =1,881 a)
•
Abb.1:
Die Größe der Planeten
Bestimmung der Planetengröße
A4: Erkläre anhand der Skizze wie die Planetengröße bestimmt werden kann. Welche
Größe aus der Skizze muss bekannt sein?
6 Gravitation
•
© Hofer
7
Bestimmung der Planetenmasse
A5: Überlege wie man mit dem 3. Keplergesetz die Masse eines Planeten bestimmen kann
und bestimme dann die Masse der Erde! (Entfernung Erde-Mond beträgt 384 000km)
•
Weitere Eigenschaften der Planeten
Die Oberflächentemperatur der Planeten wird durch Untersuchung des Lichtes, das von
Planeten ausgeht, bestimmt. Dabei zerlegt man das Licht in seine Bestandteile und
untersucht die Intensität der verschiedenen Anteile („Spektralanalyse“). Die
Spektraluntersuchungen geben zudem Aufschluss über die chemische Zusammensetzung
der Atmosphäre eines Planeten.
Die Beobachtungsdaten der Weltraumsonden liefern umfangreiches Material für die
Erforschung der Planeten.
6.3
Das Gravitationsfeld(campo (el)
de gravitación)
6.3.1
Der Feldbegriff(concepto (el) del campo)
Ein Feld liegt vor, wenn man jeden Punkt des betrachteten Raumes eine bestimmte
Eigenschaft zuordnen kann.
Beispiele: Theaterplätze
Wetterkarte
Helligkeitsverteilung einer Lampe
A1: Erkläre die drei oben angeführten Beispiele und gib an um welche Art von Feld es
sich dabei handeln könnte!
6.3.2
Gravitation und Feldbegriff
A2: Warum läuft der Mond um die Erde?
Ein Raum, in dem in jedem Punkt eine Kraft wirkt, heißt Kraftfeld.
Handelt es dabei um Gravitationskraft, so spricht man von einem Gravitationsfeld.
Dieses tritt in der Umgebung aller Massen auf.
6 Gravitation
© Hofer
6.3.3 Die Gravitationsfeldstärke(intensidad (la) del campo gravitacional)
A1: Die Erdbeschleunigung g ist auf der Erde nicht konstant.
Gib an, wovon der Betrag der Fallbeschleunigung abhängt!
Zur Darstellung des Gravitationsfeldes der Erde verwenden wir Feldlinien. Sie verlaufen
radial.
Abb1.:Gravitationsfeld
A1: Wie erkennst du in der Abb.1 wo das Gravitationsfeld stärker ist?
Die Größe der Erdbeschleunigung ist ein Maß für die Stärke des Gravitationsfeldes.
Wir bezeichnen die Erdbeschleunigung als Gravitationsfeldstärke.
A2: Leite die Formel der Gravitationsfeldstärke her!
Gravitationsfeldstärke(intensidad (la) del campo gravitacional)
a=
G.M
r2
a…Betrag der Gravitationsfeldstärke
G…Gravitationskonstante
M…Masse des Zentralkörpers
r…Entfernung von Massenmittelpunkt des Zentralkörpers
8