Lorentzkraft und magnetische Felder

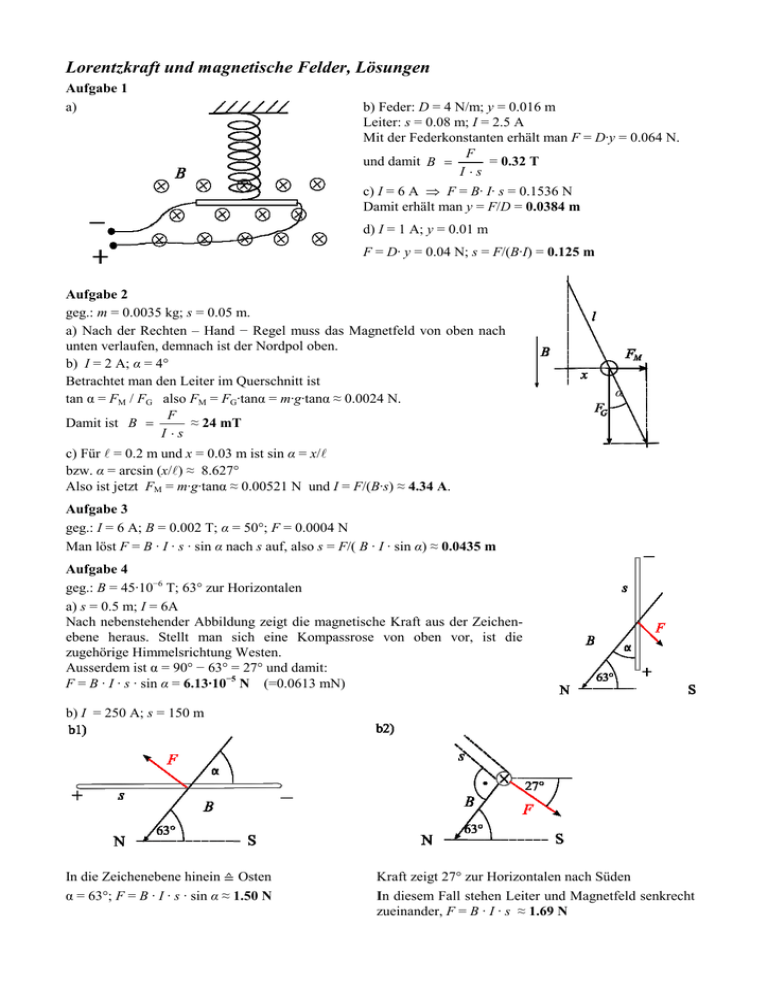
Lorentzkraft und magnetische Felder, Lösungen
Aufgabe 1
a)
b) Feder: D = 4 N/m; y = 0.016 m
Leiter: s = 0.08 m; I = 2.5 A
Mit der Federkonstanten erhält man F = D∙y = 0.064 N.
F
und damit B =
= 0.32 T
I ⋅s
c) I = 6 A ⇒ F = B∙ I∙ s = 0.1536 N
Damit erhält man y = F/D = 0.0384 m
d) I = 1 A; y = 0.01 m
F = D∙ y = 0.04 N; s = F/(B∙I) = 0.125 m
Aufgabe 2
geg.: m = 0.0035 kg; s = 0.05 m.
a) Nach der Rechten – Hand − Regel muss das Magnetfeld von oben nach
unten verlaufen, demnach ist der Nordpol oben.
b) I = 2 A; α = 4°
Betrachtet man den Leiter im Querschnitt ist
tan α = FM / FG also FM = FG∙tanα = m∙g∙tanα ≈ 0.0024 N.
F
Damit ist B =
≈ 24 mT
I ⋅s
α
c) Für l = 0.2 m und x = 0.03 m ist sin α = x/l
bzw. α = arcsin (x/l) ≈ 8.627°
Also ist jetzt FM = m∙g∙tanα ≈ 0.00521 N und I = F/(B∙s) ≈ 4.34 A.
Aufgabe 3
geg.: I = 6 A; B = 0.002 T; α = 50°; F = 0.0004 N
Man löst F = B ∙ I ∙ s ∙ sin α nach s auf, also s = F/( B ∙ I ∙ sin α) ≈ 0.0435 m
Aufgabe 4
geg.: B = 45∙10−6 T; 63° zur Horizontalen
a) s = 0.5 m; I = 6A
Nach nebenstehender Abbildung zeigt die magnetische Kraft aus der Zeichenebene heraus. Stellt man sich eine Kompassrose von oben vor, ist die
zugehörige Himmelsrichtung Westen.
Ausserdem ist α = 90° − 63° = 27° und damit:
F = B ∙ I ∙ s ∙ sin α = 6.13∙10−5 N (=0.0613 mN)
b) I = 250 A; s = 150 m
In die Zeichenebene hinein ≙ Osten
α = 63°; F = B ∙ I ∙ s ∙ sin α ≈ 1.50 N
Kraft zeigt 27° zur Horizontalen nach Süden
In diesem Fall stehen Leiter und Magnetfeld senkrecht
zueinander, F = B ∙ I ∙ s ≈ 1.69 N
Aufgabe 5
geg.: I = 20 A
µ0 ⋅ I
= 8∙10−5 T = 80 μT
2π r
µ ⋅I
b) B = 45∙10−6 T; r = 0
≈ 0.0889 m
2π ⋅ B
c) r = 0.08 m
Auf die Kompassnadel wirkt einerseits in Ost – West – Richtung das Feld des
Leiters, auf der anderen Seite in Süd – Nord – Richtung die horizontale
Komponente des Erdmagnetfeldes (vgl. Skizze)
µ ⋅I
= 50 μT; BE hor = BE∙cos (63°) ≈ 20.43 μT.
Es ist BLeiter = 0
2π r
Daraus erhält man z.B. mit α = arctan (BLeiter/BE hor) ≈ 67.78° den Winkel
zwischen BRes und der Süd−Nord−Richtung.
a) r = 0.05 m; B =
von oben:
Aufgabe 6
geg.: U = 1200 V; P = 800 000 W; r = 3.5 m
µ0 ⋅ I
≈ 38.1 μT.
2π r
Diese Feldstärke ist betragsmässig vergleichbar mit dem Erdmagnetfeld, daher wird eine Kompassnadel
darauf reagieren.
Aus P = U∙I berechnet man den Strom I = P/U = 666.7 A und damit wieder B =
Aufgabe 7
I1 = 10 A, I2 = 20 A; Mit B =
µ0 ⋅ I
erhält man jeweils bei
2π r
a) gleichgerichteten Strömen:
BP = B1 + B2 ≈ 40 μT + 26.7 μT = 66.7 μT (r1 = 0.05 m; r2 = 0.15 m)
BQ = B2 − B1 = 80 μT − 40 μT = 40 μT (r1 = r2 = 0.05 m)
BR = B1 + B2 ≈ 13.3 μT + 80 μT = 93.3 μT (r1 = 0.15 m; r2 = 0.05 m)
b) entgegengesetzen Strömen:
BP = B1 − B2 ≈ 13.3 μT
BQ = B1 + B2 = 120 μT
und
BR = B2 − B1 ≈ 66.7 μT
Aufgabe 8
geg.: r = 0.01 m; l = 1 m; F = 1 N
Die (gegenseitige) Kraft der Leiter beträgt F = B ⋅ I ⋅ l =
und daher ist I =
2π ⋅ r ⋅ F
µo ⋅ l
µ0 ⋅ I
⋅I ⋅l =
2π ⋅ r
µ0 ⋅ I 2 ⋅l
2π ⋅ r
≈ 223.6 A.
Aufgabe 9
a) von oben:
Innerhalb der Spule ergibt sich ein Feld in Ost – West – Richtung, die
Nadel richtet sich nach dem resultierenden Magnetfeld aus.
b) geg.: N = 40; l = 0.3 m
BSp = μ0 ∙ N ∙ I / l; BE hor = BSp/tan(α) ergibt:
I [mA]
0
30
60
90
120
150
180
α [deg]
0
13
25
34
43
50
55
BSpule [μT]
0
5.03
10.05
15.1
20.1
25.1
30.2
BErde [μT]
-
21.79
21.55
22.39
21.55
21.06
21.15
Aufgabe 10
a) Die Kräfte auf den oberen bzw. den unteren Teil des Leiterrahmens kompensieren sich.
b) B = μ0 ∙ N ∙ ISp / l ≈ 0.01257 T; F = n ∙ B ∙ IR ∙ s ≈ 0.01 N
Aufgabe 11
geg.: Spule: l = 0.6 m; d = 0.15 m; N = 700; Leiterstück: s = 0.12 m
a) I2 = 20 A; F = 0.009 N; ges.: I1
Aus der Kraftwirkung auf den Leiter kann man das Magnetfeld bestimmen: B = F/(I2 ∙ s) = 0.00375 T
Spule: B =
µ 0 ⋅ N ⋅ I1
l2 + d 2
⇔ I1 =
B ⋅ l2 + d 2
µ0 ⋅ N
≈ 2.64 A
b) F = 0.009 N; I1 = I2 = I = ?
Gleichsetzen der beiden Formel für B ergibt
µ0 ⋅ N ⋅ I
l2 + d 2
=
F
I ⋅s
⇔ I =
F ⋅ l2 + d 2
µ0 ⋅ N ⋅ s
≈ 7.26 A