1. Zahlenbereiche - Fakultät für Mathematik

Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
51 722 Elementarmathematik (LH)
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
und Fehlerfreiheit
1. Zahlenbereiche
1.4
Die Reellen Zahlen
1.4.1. Definition
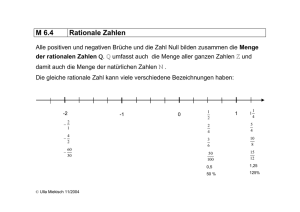
Die Zahlenbereichserweiterungen von IN auf ZZ und ZZ auf Q
I gingen von der Nichtabgeschlossenheit der Subtraktion bzw. der Division aus. Damit sind im Bereich von Q
I die vier Grundrechenarten abgeschlossen. Zugleich sind damit auch alle linearen Gleichungen lösbar.
Dies gilt jedoch nicht für quadratische Gleichungen der Form x2 = a, wenn a keine Quadratzahl ist.
Beispiel: x2 = 5
x∉ Q
I
Die Menge aller Zahlen a fasst man zur Menge J der irrationalen Zahlen zusammen. Eine Zahl
heißt irrational, wenn sie sich nicht durch einen vollständig gekürzten Bruch darstellen lässt.
1.4.2. Geometrischer Nachweis einer irrationalen Zahl
Quadratwurzel
2
Es soll geklärt werden, ob die Gleichung x2 = a auch dann eine Lösung hat, wenn a keine Quadratzahl ist. Hierzu suchen wir auf zeichnerischem Weg die Maßzahl der Seitenlänge eines Quadrats
mit dem Flächeninhalt 2 FE.
Die beiden Einheitsflächen werden zerlegt und neu zusammengesetzt. Die Seite mit der Längenmaßzahl b wird dann auf die Zahlengerade gedreht.
x2 = 1
1 FE
1 LE
x2 = 2
zerlegungsgleich
2 FE
2
x =1
1 FE
b LE
0
1
b
2
Es gibt also ein Quadrat, bei dem die Maßzahl b der Seitenlänge eines Quadrats die Gleichung
x2 = 2 erfüllt. Diese Zahl b heißt Quadratwurzel. Ihr kann ein Punkt auf der Zahlengeraden zugeordnet werden. Er liegt zwischen 1 und 2. Wir schreiben für diese Zahl 2 .
Quadratwurzel aus a
I haben zwei Lösungen, wenn a eine Quadratzahl ist. Wir
Gleichungen der Form x2 = a mit a ∈ Q
fordern, dass jede solche Gleichung auch dann zwei Lösungen haben soll, wenn a keine Quadratzahl, aber positiv ist. Die Lösungen unterscheiden sich nur im Vorzeichen. Die nicht negative dieser
beiden Lösungen bezeichnet man als Quadratwurzel aus a. Die Zahl a heißt Radikand.
1.4.3. Nachweis der Irrationalität
a) algebraisch
Für den Nachweis, dass
2 keine rationale Zahl ist, verwenden wir einen so genannten Wi-
derspruchsbeweis. Hierzu nehmen wir an, 2 sei eine rationale Zahl. Führt diese Annahme
auf einen Widerspruch, so kann nur die Annahme falsch sein, also muss das Gegenteil der Annahme wahr sein.
Behauptung:
2 ist keine rationale Zahl.
Annahme:
2 sei eine rationale Zahl.
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
und Fehlerfreiheit
Beweisgang: Aufgrund der Annahme lässt sich
2 als Bruch
p
q
mit teilerfremdem
p, q ∈ IN schreiben.
p
q
b)
= 2
⇒
()
p
q
2
= 2
⇔
p2
q2
=2
⇔
p2 = 2q2
p2 = 2q2
Da q ∈ IN, ist 2q2 eine durch 2 teilbare natürliche Zahl und
demnach auch p2. Wenn aber p2 durch 2 teilbar ist, dann auch
p und es gilt: p = 2k mit k ∈ IN.
⇔ 2k2 =
Einsetzen in die Gleichung ergibt:
(2k)2 = 2q2
2
q
q2 = 2k2
Nach derselben Überlegung wie oben kann gezeigt werden,
dass q eine gerade Zahl ist. Zwei gerade Zahlen haben aber
immer den Teiler 2 gemeinsam, sie sind also nicht teilerfremd.
Dies ist ein Widerspruch zur Annahme. Deshalb ist ihr Gegenteil, also die Behauptung, wahr.
Folgerung:
2 ist keine rationale Zahl. Man bezeichnet sie als irrationale
Zahl.
geometrisch
Die Entdeckung der Irrationalität von 2 geht auf Hippasos von Metapont zurück. Er war
ein griechischer Mathematiker und Musiktheoretiker aus dem Kreis der Pythagoreer und lebte um 350 v. Chr.
Der Wissenschaftsbund der Pythagoreer glaubte, dass alles
durch Zahlen ausdrückbar sei. So hatten sie richtigerweise erkannt, dass bei Saiteninstrumenten Tonintervalle durch ganzzahlige Verhältnisse festzulegen sind. Man erhöht nämlich bei sole
a
chen Instrumenten die Tonhöhe, indem man die Länge des
Quart 3 : 4
schwingenden Teils der Saite verkürzt. Solche Zahlenpaare
nannten die Griechen "aussprechbare" Zahlen.
Auch für die Bestimmung des größten gemeinsamen Teilers
(ggT) zweier Zahlen hatten die Pythagoreer ein besonderes Verfahren entwickelt:
Schreibe die beiden Zahlen an. Schreibe in die nächste Zeile die
kleinere der beiden Zahlen und den Differenzwert der beiden.
Nach einer gewissen Anzahl von Schritten bricht dieses Verfahren ab. Die letzte von null verschiedene Zahl ist der ggT. Die Pythagoreer sprachen vom "gemeinsamen Maß" zweier Zahlen.
63
35
35
28
28
7
7
21
7
14
7
7
7
0
ggT (63; 35) = 7
Hippasos fand nun mittels einer geometrischen Konstruktion, dass es auch Maßzahlenpaare gibt, für die ein gemeinsames Maß nicht angegeben werden kann.
Ein Gedankengang zum Auffinden eines solchen
Zahlenpaares ohne gemeinsames Maß ist nachfolgend skizziert.
CC
D
F
G
d
E
a
Aus der Kongruenz der Dreiecke ABE und AEF
folgt:
BE = EF
Δ CFE ist gleichschenklig-rechtwinklig. Also gilt:
A
a
B
FC = EF
Δ CFE kann also zum Quadrat CFEG ergänzt
werden.
Im Quadrat CFEG kann obige Konstruktion wiederholt werden. Man erhält immer wieder ein
Quadrat, die Konstruktion wiederholt sich ständig, bricht also nie ab. Demnach lässt sich für
die Längen der Quadratdiagonalen und der Quadratseite kein gemeinsames Maß finden.
Die Pythagoreer nannten solche Zahlenpaare "unaussprechbar". In späteren lateinischen
Übersetzungen wurde dafür das Wort "irrationalis" verwendet. Davon leitet sich unsere heutige Bezeichnung "irrationale Zahlen" ab. Bereits Euklid konnte beweisen, dass 2 keine
rationale Zahl ist. Die griechischen Mathematiker lehnten aber den Umgang mit diesen Zahlen aus philosophischen Gründen ab.
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
c)
und Fehlerfreiheit
Plausibler Nachweis für Dezimalzahl
Die Zahl
2 kann nicht auf 0 enden, denn sonst könnte die Zahl um eine Stelle gekürzt
2 nicht mit 0 endet, kann aber auch ihr Quadrat ( 2 )2 nicht mit 0
werden. Wenn die Zahl
enden. Die Zahl
2 ist also keine endliche Dezimalzahl.
Da ( 2 )2 = 2 gilt, kann man folgende Überlegung anstellen:
Endziffern
beim
Quadrieren
02
12
22
32
42
0
1
4
9
6
5
a
1,2
1,3
1,4
1,5
1,6
Es gilt: 1,96 <
⇒
92
82
72
62
1,4 <
a2
1,44
1,69
1,96
2,25
2,56
2
< 2,25
2 < 1,5
52
1.4.4. Näherungsverfahren
a)
Intervallschachtelung
Wir grenzen die Zahl 2 durch Doppelungleichungen ein, indem wir die Quadrate der
Grenzen verschiedener Intervalle betrachten.
Es gilt
1. Näherung:
a <
1 <
x
2
2. Näherung:
1,4 <
2
a2 < x2 < b2
12 < 2 < 22
< b
< 2
denn
denn
< 1,5
denn
1,42 <
2
2 < 1,52
3. Näherung:
1,41 <
2
< 1,42
denn
1,41
<
2 < 1,422
4. Näherung:
1,414 <
2
< 1,415
denn
1,4142
<
2 < 1,4152
Diese Folge von Intervallen lässt sich beliebig fortsetzen. Dabei wird die Intervalllänge mit
jeder Näherung kleiner. Jedes Intervall liegt vollständig im vorangehenden und 2 liegt in
jedem Intervall. Eine solche Folge von Intervallen heißt Intervallschachtelung.
1,4 1,41
1,414
1,42
1,5
1,415
Mit Hilfe der Intervallschachtelung lässt sich für jede Quadratwurzel ein beliebig genauer
Näherungswert ermitteln.
b)
Heron-Verfahren
Heron lebte um 75 n. Chr. in Alexandria. Er gibt ein Verfahren
an, nach dem für irrationale Zahlen rationale Näherungswerte
mit beliebiger Genauigkeit ermittelt werden können.
Hierzu suchen wir die Seitenlängen eines Quadrats mit dem
Flächeninhalt a, d.h. wir suchen eine Zahl x als Näherungswert
für a mit a ∈ QI 0+ .
Wenn a keine Quadratzahl ist, so existiert keine rationale Zahl,
die mit sich selbst multipliziert den Wert a ergibt. Wir zerlegen
deshalb a in das Produkt x1 ⋅ y1 (Ausgangsrechteck). Wählt man
nun für x1 einen Näherungswert, so lässt sich y1 mit dem Taschenrechner berechnen.
Mit diesem Verfahren kann man die Zahl x als Lösung der
quadratischen Gleichung x2 = a in der Regel beliebig genau annähern (Zielquadrat).
Ausgangsrechteck
Zielquadrat
a
y1
a x2
x1
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
und Fehlerfreiheit
x1 ⋅ y1 = a
a
y1 =
x1
Zerlegen des Radikanden a:
Wählen eines beliebigen, sinnvollen
1. Näherungswertes x1 und Berechnen von y1:
Bilden des Mittelwertes:
x2 =
a
x1
Ersetzen von y1 durch
(2. Näherungs-
:
(n + 1) - ter Näherungswert:
1
2
(x1 + y1)
)
x2 =
1
2
(x
1
+
a
x1
xn + 1 =
1
2
(x
n
+
a
xn
)
Durch Bilden des Mittelwertes verbessert sich im Allgemeinen bei jedem Schritt der Näherungswert für a .
c)
Näherung über das Binom (x + ∆x)2
Wir setzen x + ∆x = 2 und x = 1
Durch Quadrieren erhalten wir: (1 + ∆x)2 = 1 + 2∆x + ∆x2 = 2
Vernachlässigen von ∆x2:
1 + 2∆x = 2
⇔
∆x = 0,5
1. Näherung
x1 = 1,5
Überprüfung ergibt:
1,4 < 2 < 1,5
Diese Verfahren kann beliebig fortgesetzt werden.
1.4.5. Definition der reellen Zahlen
Die Menge aller rationalen und aller irrationalen Zahlen heißt Menge der reellen Zahlen.
Man bezeichnet sie mit IR .
Jeder reellen Zahl entspricht genau ein Punkt der Zahlengeraden. Jedem Punkt der Zahlengeraden entspricht genau eine reelle Zahl.
− 2
−5
−4
−3
−2
π
2
−1
0
1
2
3
4
1.4.6. Übersicht über das Zahlensystem
Auch die bisher bekannten Zahlen können in der Wurzelschreibweise dargestellt werden.
Natürliche Zahlen:
5 =
Rationale Zahlen:
+
IR :
IR –:
25
−5 = − 25
Ganze Zahlen:
25
9
Menge der positiven reellen Zahlen
Menge der negativen reellen Zahlen
5
3
=
I
IR Q
ZZ
IN
IR 0+ = IR + ∪ {0}
IN ⊂ ZZ ⊂ Q
I ⊂ IR
1.4.7. Fachsprachliche Anmerkungen zu IR
1.
Die Ausdrucksweise und Schreibweise
2 = 1,4142 ist eigentlich nicht korrekt, jedoch üblich.
1.4.8. Kulturhistorische Anmerkungen
Die Araber rechneten insbesondere beim Lösen von Gleichungen seit dem 9. Jahrhundert schon
mit irrationalen Zahlen. Sie hatten erkannt, dass sich mit diesen Zahlen bestimmte nicht lineare
Gleichungen lösen ließen.
Im 12. Jahrhundert kam das Wissen über irrationale Zahlen auch zu den Mathematikern nach Mitteleuropa. Leonardo von Pisa (etwa 1180 - 1250) war einer der ersten, der sich mit diesen Zahlen
beschäftigte.Erst um 1850 waren die irrationalen Zahlen in der Mathematik voll anerkannt.
Das Wurzelzeichen entstand als Abkürzung r für das lateinische Wort „radix“. Die Verlängerung mit
Endhaken verdeutlichte, über welchen mathematischen Zeichen sich das Wurzelzeichen erstrecken sollte.
radix 4x + 3
r 4x + 3
4x + 3
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
51 722 Elementarmathematik (LH)
und Fehlerfreiheit
1.4.9. Übungsblatt: Reelle Zahlen
Aufgabe 1
1.
Schreiben Sie ein Programm in Excel zur Intervallschachtelung von
2.
Aufgabe 2
2.
Schreiben Sie ein Programm in Excel zum Heron-Verfahren von
2.
Aufgabe 3
3.
Geben Sie nach einem beliebigen Verfahren einen Näherungswert für x =
3 an.
Aufgabe 4
4.0
R
Gegeben ist das Quadrat ABCD mit a = 5 cm. Die Quadratseiten [AB], [BC], [CD] und [DA] werden über B, C, D, A hinaus um eine Strecke der Länge b = 3 cm verlängert. Die
entstehenden Punkte bilden das Viereck PQRS.
Zeige: Viereck PQRS ist ein Quadrat.
Berechne den Flächeninhalt und die Seitenlänge des
Quadrats PQRS (auf zwei Dezimalen gerundet).
4.1
4.2
Aufgabe 5
C
b
a
A
a
b
B
b
P
Geben Sie eine mögliche Zahl an, die durch die Intervallschachtelung dargestellt wird.
a)
]–2
;
–1[
b)
]0
;
1[
]–1,3
;
–1,1[
]0,6
;
0,7[
]–1,21
;
–1,19[
]0,63
;
0,64[
]–1,201
;
–1,199[
]0,636
;
0,637[
]–1,2001
;
–1,1999[
]0,6363
;
0,6364[
5
Aufgabe 6
6
b
D
S
Zeigen Sie, dass gilt:
a)
a +
b)
10 +
b =
a +b + 2 a⋅b
24 +
40 +
60 =
> b
a =
( 2 +
3 +
5)2
Q
Universität Regensburg
Naturwissenschaftliche Fakultät I – Didaktik der Mathematik
Dr. Günter Rothmeier
WS 2008/09
51 722 Elementarmathematik (LH)
Lösungen zu Übungsblatt 1.4:
Private Vorlesungsaufzeichnungen
Kein Anspruch auf Vollständigkeit
und Fehlerfreiheit
Reelle Zahlen
Zu Aufgabe 1
individuelle Lösung
Zu Aufgabe 2
individuelle Lösung
Zu Aufgabe 3
individuelle Lösung
Zu Aufgabe 4
ΔAPQ ≅ ΔBQR ≅ ΔCRS ≅ ΔDSP
⇒
PQ = QR = RS = SP
<) AQP + <) QPA = 90°. Also ist auch <) QPS = 90°.
Also ist Viereck PQRS ein Quadrat.
AΔPQA = a2 + 4 ⋅ 21 ⋅ (a + b) ⋅ b = a2 + 2ab + 2b2 = (a + b)2 + b2
APQRS = 64 cm2 + 9 cm2 = 73 cm2
PQ = 73 cm ≈ 8,54 cm
4.1
4.2
Zu Aufgabe 5
5
a)
–1,2
5
11
b)
Zu Aufgabe 6
6
a)
b )2 =
( a +
b) ( 2 +
2+
10 +
3 +
6 +
5 )2 =
10 +
24 +
a + b + 2 ab
6 +3+
40 +
60
15 +
10 +
15 + 5 =