Strom (Elektrisch) Spannung (Elektrisch) Widerstand (Elektrisch)

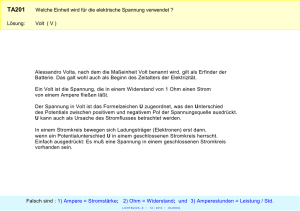
Strom (Elektrisch)
Als elektrischen Strom bezeichnet man die Bewegung von Ladungsträgern durch
einen Stoff oder durch einen luftleeren Raum. Ladungsträger sind zum Beispiel
Elektronen oder Ionen. Bewegen sich also Elektronen zum Beispiel durch einen
Kupferdraht, spricht man von Stromfluss. Stellt euch das wie einen Fluss (Wasser)
in der Natur vor. Dort fließt auch Wasser in einem Flussbett. Und so fließen
Elektronen in einem Kupferdraht.
Nun benötigt man natürlich noch eine Angabe, wie viel Strom denn überhaupt fließt.
Diese Angabe wird in Ampere gemacht, benannt nach dem französischen Physiker
und Mathematiker André Marie Ampère. Die Stromstärke wird als Formelzeichen mit
"I" angegeben. Beispiel: I = 4 Ampere. Oftmals wird statt Ampere einfach A
geschrieben. Dies verkürzt die Schreibweise zu: I = 4 A. Ob 4 Ampere viel oder
wenig ist, hängt von der jeweiligen Anwendung ab.
Spannung (Elektrisch)
Für viele Dinge im Leben gibt es Voraussetzungen: Damit ein Mensch überleben
kann, muss er atmen. Auch für den Strom gibt es Voraussetzungen. So benötigt der
Strom zum fließen eine Spannung. Unter der elektrischen Spannung versteht man
die treibende Kraft, die die Ladungsbewegung verursacht. Grundsätzlich gilt: Je
höher die Spannung, desto mehr Strom kann fließen.
Auch für die Spannung hat man ein Formelzeichen, das "U". Die Spannungshöhe
wird in Volt angegeben. U = 5 Volt. Oder etwas kürzer geschrieben: U = 5 V. Auch
hier gilt: 5 Volt kann sehr viel oder sehr wenig sein, es hängt immer von der
Anwendung ab. Für die Geräte im Haushalt wäre es viel zu wenig. Der Anschluss der
Hausleitung hat 230 Volt (Effektiv allerdings, aber damit beschäftigen wir uns in
einem späteren Kapitel).
Widerstand (Elektrisch)
Der Widerstand ist sozusagen der "Gegner" der Spannung. Denn an jedem
Widerstand fällt Spannung ab, sprich wird weniger. Und wir haben ja bereits bei
Spannung gesagt: Je geringer die Spannung, desto weniger Strom kann fließen (bei
gleichem Widerstandswert). Ein Widerstand ist ein elektronisches Bauteil, das es
für (sehr wenig) Geld zu kaufen gibt. Auch ein elektronischer Leiter, zum Beispiel ein
Kupferdraht hat einen eigenen Widerstand, an dem Spannung abfällt. Oder noch
etwas allgemeiner ausgedrückt: Materialien haben einen Widerstandswert. Allerdings
interessiert man sich in der Elektrotechnik in der Regel für den Widerstand eines
Bauteils, einer Leitung oder einer anderen Schaltungskomponente. Die Angaben
Strom, Spannung und Widerstand lassen sich über das Ohm’sche Gesetz berechnen
(wird im folgenden Kapitel behandelt).
Der Widerstand - meist kurz mit "R" abgekürzt - ist ein Maß dafür, wir stark
Elektronen gebremst werden. Die Höhe des Widerstandes wird in Ohm angegeben.
Beispiel: R = 10 Ohm. Für diesen Ausdruck gibt es auch noch eine kürzere
Schreibweise: R = 10Ω. Auch hier gilt: Ob 10 Ohm viel oder wenig sind, hängt von
der Anwendung ab. Dazu mehr in den kommenden Kapiteln zu den Grundlagen der
Elektrotechnik.
Ohm’sches Gesetz
Ohm’sche Gesetz Formel/Gleichung:




Formel: U = R · I
"U" ist die Spannung in Volt, z.B. 1 V
"R" ist der Widerstand in Ohm, z.B. 1 Ω
"I" ist der Strom in Ampere, z.B. 1 A
Beispiel: Der Widerstand beträgt 10 Ohm und es fließen 5 Ampere. Wie groß ist die
Spannung? Antwort: U = 10 Ohm · 5 Ampere = 50 Volt. Oder in Kurzform: U = 10 Ω ·
5 A = 50 V. Die Spannung beträgt somit 50 Volt. Hat man also zwei der drei Größen,
kann man damit die dritte Größe berechnen.
Anwendung zum Ohm’schen Gesetz
Ich möchte euch hier noch eine Anwendung zum Ohm’schen Gesetz zeigen. Dabei
geht es um einen kleinen Stromkreis. Dieser beinhaltet eine Spannungsquelle,
welche die benötigte Spannung erzeugt. Zu dem gibt es einen Widerstand und
Kupferdrähte, welche die Spannungsquelle mit dem Widerstand verbinden. Bevor wir
jedoch den Stromkreis zeigen, zunächst die drei dafür wichtigen Symbole.
Symbol
Bedeutung
Symbol für eine Spannungsquelle.
Symbol für einen Widerstand.
Symbol für einen Leiter (z. B. Kupferleitung)
Und dies alles wird nun zu einem kleinen Stromkreis zusammengebaut. Dies sieht
dann wie folgt aus:
Wichtige Anmerkung: In der Elektrotechnik wird die Stromrichtung von "+" nach "-"
angegeben. In der Physik ist dies meist umgekehrt. Das ist für Anfänger der
Elektrotechnik äußerst verwirrend, aber so wird es (leider) gehandhabt. Da wir hier
Dinge aus der Elektrotechnik besprechen, fließt der Strom von "+" nach "-" !
Der Strom fließt in diesem Bild somit "oben" aus der Spannungsquelle raus, den
Leiter entlang durch den Widerstand, und über die beiden Ecken nach unten in den
Minus-Anschluss der Spannungsquelle. Ansonsten gilt auch hier das Ohm’sche
Gesetz: U = R · I. In manchen Fällen schreibt man auch noch hin, wie groß der
Widerstand ist, wie viel Strom fließt oder wie groß die Spannung ist.
Elektrische Leistung
Je mehr Leistung an einem Widerstand abfällt, desto wärmer wird dieser. Ab
einem gewissen Punkt geht dieser sogar kaputt, sprich brennt durch. Wie viel
Leistung umgesetzt wird, lernt ihr hier zu berechnen. Dieser Artikel gehört zum
Bereich Elektrotechnik bzw. Physik.
Die elektrische Leistung "P" - zum Beispiel an einem Widerstand - ist das Produkt
aus Strom mal Spannung. Die elektrische Leistung wird in Watt angegeben. Bevor
wir die Formel jedoch noch näher auseinander nehmen, zunächst wieder der Hinweis
auf Artikel, die zum Verständnis der elektrischen Leistung als Voraussetzung gelten.
Wem die folgenden Dinge noch nichts sagen, der sollte diese erst einmal nachlesen.
Elektrische Leistung berechnen
Wie bereits angesprochen, berechnet sich die elektrische Leistung aus Strom ·
Spannung und wird in Watt - kurz W - angegeben. Beispiel: Wir haben 20 Volt
Spannung anliegen und 10 Ampere Strom fließen. Damit ist die Leistung: P = U · I =
20 Volt · 10 Ampere und damit P = 200 Watt, kurz 200 W. Unter Nutzung des
Ohm’schen Gesetzes kann man auch noch weitere Formeln einsetzen. Es folgen nun
einige Formeln, mit denen man die elektrische Leistung berechnen kann.
Elektrische Leistung Formel 1:




Formel: P = U · I
"P" ist die Leistung in Watt
"U" Ist die Spannung in Volt
"I" ist der Strom in Ampere
Technische Stromrichtung
Die technische Stromrichtung beruht auf einer Konvention, bei der man annahm, dass der
elektrische Strom vom Pluspol einer Spannungsquelle durch den Stromkreis zum Minuspol
fließt. Diese Richtung wird auch heute noch als konventionelle oder technische
Stromrichtung bezeichnet und in Schaltbildern verwendet.
Tatsächlich bewegen sich in einem Stromkreis die negativ geladenen Elektronen vom
Minuspol einer Spannungsquelle durch den Stromkreis zum Pluspol. Am Minuspol herrscht
Elektronenüberschuss, am Pluspol Elektronenmangel. Diese Stromrichtung nennt man
physikalische Stromrichtung.
Physikalische Stromrichtung
In einem geschlossenen Stromkreis werden freie Elektronen vom negativen Pol einer
Spannungsquelle abgestoßen und vom positiven Pol angezogen. Dadurch entsteht
ein Elektronenstrom vom negativen Pol durch die Leitung zum positiven Pol.
Merke:
Technische Stromrichtung von plus nach minus.
Physikalische Stromrichtung von minus nach plus.
Spannungserzeugung
Arten der Spannungserzeugung
Es gibt insgesamt 6 Arten der Spannungserzeugung:






Spannung durch Induktion (Generator, Dynamo)
Spannung durch Licht (Solarzellen)
Spannung durch Elektrochemie (Batterie, Akku)
Spannung durch Druck oder Zug (Piezoelemente)
Spannung durch Wärme (Thermoelemente)
Spannung durch Reibung (Bandgenerator)
Wird eine Leiterschleife in einem Magnetfeld so bewegt, dass sich der magnetische
Fluss in der Leiterschleife ändert, so wird in ihr während der Bewegungsdauer eine
Spannung erzeugt. Dies nennt man Induktion.
Die Richtung, also die Polung der erzeugten Spannung hängt von der
Bewegungsrichtung des Leiters als auch von der Richtung des Magnetfeldes ab.
Die Höhe der erzeugten Spannung wird umso größer, je schneller sich die
Leiterschleife bewegt oder sich der magnetische Fluss ändert.
In der Praxis benutzt man zur Spannungserzeugung allerdings keine einzelnen
Leiterschleifen, sondern viele Leiterschleifen, die zusammen eine Spule ergeben.
Wenn sich eine Spule in einem Magnetfeld dreht, dann wird in ihr ebenfalls
fortlaufend eine Spannung erzeugt. Auch hier ist die erzeugte Spannung eine
Wechselspannung, genauer gesagt eine sinusförmige Wechselspannung. Jeder
Dynamo funktioniert nach diesem Prinzip. Dynamos in sehr großem Umfang nennt
man Generatoren. Letztere befinden sich z. B. in den Kraftwerken und werden durch
Turbinen angetrieben.
Dreht sich eine Spule in einem Magnetfeld, so wird in ihr ebenfalls eine Spannung
erzeugt. Die erzeugte Spannung nimmt mit steigender Windungszahl der Spule
sowie mit steigender Drehgeschwindigkeit der Spule zu.
Potenzialdifferenz
Unter einer Potenzialdifferenz versteht man eine elektrische Spannung.
Reihenschaltung oder Serienschaltung von
Widerständen
Wir haben uns im letzten Abschnitt schon mit einem Widerstand in einem Stromkreis
befasst. Nun wollen wir mehrere Widerstände hintereinander schalten. Dabei sprich
man von Reihenschaltung oder Serienschaltung von Widerständen. Dies kann zum
Beispiel so aussehen:
Meist nummeriert man die Widerstände durch. So auch hier im Beispiel geschehen.
Man kann diese drei Widerstände auch zu einem einzigen Zusammenfassen. Dabei
addiert man alle Widerstände: RGesamt = R1 + R2 + R3. Ob man nun zwei, drei, vier
oder mehr Widerstände hintereinander hat, spielt keine Rolle. Einfach alle
zusammenaddieren und man hat den Gesamtwiderstand.
Reihenschaltung oder Serienschaltung Beispiel
Schauen wir uns dazu einmal ein kleines Beispiel an. Wir wollen den folgenden
Stromkreis analysieren und berechnen, wie viel Strom in dem Kreislauf fließt:
Nehmen wir folgende Werte an: R1 = 200Ω, R2 = 100Ω, R3 = 500Ω und die Spannung
ist 220 V. Die Frage lautet: Wie viel Strom fließt in dem Stromkreis? Dazu fassen wir
zunächst die Widerstände zu einem Gesamtwiderstand zusammen. RGesamt = 200 Ω
+ 100 Ω + 500 Ω = 800 Ω. Und dies setzen wir in U = R · I ein. Dies liefert: 220 V =
800 Ω · I. Man berechnet somit 220 V dividiert durch 800 Ω. Rechnet man das aus,
erhält man I = 0,275 A.
Zweite Kirchhoffsche Regel (Maschenregel)
In einem geschlossenen Stromkreis (Masche) stellt sich eine bestimmte
Spannungsverteilung ein. Die Teilspannungen addieren sich in ihrer Gesamtwirkung.
Betrachtet man die Spannungen in der Schaltung, so teilt sich die Summe der
Quellenspannungen Uq1 und Uq2 in die Teilspannungen U1 und U2 an den
Widerständen R1 und R2 auf. Der Strom I ist für die Spannungsabfälle an R1 und R2
verantwortlich.
Die Maschenregel ermöglicht die Berechnung einer unbekannten Quellenspannung.
Maschenregel: In jedem geschlossenem Stromkreis ist die Summe der
Quellenspannungen gleich der Summe aller Spannungsabfälle oder die Summe aller
Spannungen ist Null.
Parallel-Schaltung mit zwei Widerständen berechnen
Wir haben uns bereits mit der Serienschaltung - oder auch Reihenschaltung genannt
- beschäftigt. Nun kann es natürlich noch passieren, dass Widerstände nicht
hintereinander geschaltet werden, sondern parallel zu einander liegen. Dies könnte
in einer Schaltung wie folgt aussehen:
Auch in diesem Fall ist es möglich, die Widerstände zusammen zu fassen. Liegen
zwei Widerstände parallel, lautet die Formel.
Setzt zum Beispiel für R1 einmal 100 Ohm ein und für R2 200 Ohm ein. Dann solltet
ihr RGesamt = 66,66 Ohm erhalten. Ausführlich sieht das dann so aus:
Parallel-Schaltung bei mehr als zwei Widerständen
Liegen in einer Schaltung mehr als zwei Widerstände parallel, so verwendet man die
folgende Formel zur Berechnung des Gesamtwiderstandes (RGES).
Tipp: Setzt alle Widerstandswerte R1, R2... ein und berechnet damit die "rechte" Seite der
Gleichung. Im Anschluss nehmt ihr einfach den Kehrwert und erhaltet damit den
Gesamtwiderstand. Ihr müsst also - wie aus der Mathematik gewohnt - nach RGES dann
umstellen.
Erste Kirchhoffsche Regel (Knotenregel)
Bei der Parallelschaltung von Widerständen ergeben sich Verzweigungspunkte,
sogenannte Knotenpunkte, des elektrischen Stroms. Betrachtet man die Ströme um
den Knotenpunkt herum, stellt man fest, dass die Summe der zufließenden Ströme
gleich groß ist, wie die Summe der abfließenden Ströme.
Mit Hilfe der Knotenregel können unbekannte Ströme in einem Knotenpunkt
berechnet werden.
Wechselstrom und Wechselspannung
Tesla ist der Endecker von Wechselstrom und Drehstrom. Beide haben schnell
weltweite Anwendung gefunden. Ohne diese Entdeckung von Tesla, die es erst
möglich machte, elektrischen Strom über viele Hunderte von Kilometern zu
übertragen, gäbe es die heutige Selbstverständlichkeit der Elektrizität mit ihren
enorm vielseitigen Anwendungen nicht.
Bei Wechselstrom und Wechselspannung spricht man von elektrischen Größen, die
in den Einheiten Ampere (A) und Volt (V) angegeben werden, deren Werte sich im
Verlauf der Zeit (t) regelmäßig wiederholen. Der Wechselstrom ist ein elektrischer
Strom, der periodisch seine Polarität (Richtung) und seinen Wert (Stromstärke)
ändert. Dasselbe gilt für die Wechselspannung.
Es gibt verschiedene Arten von Wechselstrom. Reine Wechselgrößen sind die
Rechteckspannung, die Sägezahnspannung, die Dreieckspannung und die
Sinusspannung (Welle) oder eine Mischung aus allen diesen Varianten.
In der Elektrotechnik werden hauptsächlich Wechselspannungen mit sinusförmigem
Verlauf verwendet. Beim sinusförmigen Kurvenverlauf treten die geringsten Verluste
und Verzerrungen auf. Deshalb werden die folgenden Beschreibungen des
Wechselstromes und der Wechselspannung anhand des sinusförmigen
Kurvenverlaufs erklärt.
Wechselspannung wird durch Generatoren in Kraftwerken erzeugt. Dabei dreht sich
ein Roter im Generator um 360 Grad. Dadurch entsteht eine Spannung mit
wechselnder Polarität, also ein sinusförmiger Verlauf.
Die wichtigste Wechselspannung ist 230 Volt aus unserem Stromnetz. Es hat eine
Frequenz von 50 Hz. Das sind 50 Umdrehungen in der Sekunde eines Rotors im
Generator.
Kennwerte der Sinusspannung


Augenblickswert und Amplitude
Periode und Frequenz
Augenblickswert und Amplitude
Da eine Wechselspannung nie einen konstanten Spannungswert hat, spricht man bei
elektrischen Wechselgrößen, deren Zeitabhängigkeit gezeigt werden soll, von
Augenblickswerten (Momentanwerte). Diese Augenblickswerte werden durch einen
Kleinbuchstaben (Formelzeichen) angegeben.
Maximal- bzw. Scheitelwerte der Amplitude von sinusförmigen zeitabhängigen
Wechselgrößen werden durch ein Dach über dem Formelzeichen gekennzeichnet.
Beispiele dazu wären die Spannung û (sprich: u-Dach) und der Strom î (sprich: iDach).
Bei bekanntem Scheitelwert lässt sich bei jedem beliebigen Drehwinkel λ ( = 0° ...
360°) der Augenblickswert berechnen.
Periode und Frequenz
Die positive und die negative Halbwelle einer Schwingung bezeichnet man als
Periode. Die Zeit die zum Durchlaufen der Periode benötigt wird ist die
Periodendauer Τ. Die Periodendauer Τ wird in Sekunden angegeben.
Die Frequenz gibt die Zahl der Perioden an, die in einer Sekunde durchlaufen
werden. Die Frequenz wird in Hertz (Hz) angegeben.
Die Frequenz ist der Kehrwert der Periodendauer. Das bedeutet, die Frequenz ist um
so größer, je kleiner die Periodendauer ist.
Kennwerte einer Sinuskurve
Effektivwert einer Wechselspannung
Der Wert einer (sinusförmigen) Wechselspannung ändert sich dauernd. Zu manchen
Zeitpunkten hat die Wechselspannung ihren Maximalwert erreicht, zu anderen
Zeitpunkten ist der Spannungswert gerade Null.
Zu anderen Zeitpunkten liegt der Spannungswert irgendwo dazwischen.
Dieser Wechsel macht eine Aussage über den Wert einer Wechselspannung im
Gegensatz zu einer Gleichspannung, bei der der Spannungswert konstant ist,
schwierig.
Um Wechselspannungen vergleichen zu können nutzt man den sogenannten
Effektivwert.
Der Effektivwert
Um den Begriff Effektivwert zu verstehen, betrachtet man am einfachsten die
Spannung und den Strom an einem ohmschen Widerstand.
Zur Bestimmung des Effektivwertes betrachtet man nun die Leistung, die an diesem
ohmschen Widerstand umgesetzt wird.
Auch der Momentan Wert dieser Leistung schwankt.
Man kann aber den Mittelwert dieser Leistung bestimmen.
Der Effektivwert einer Spannung ist dann genau die Gleichspannung, die an
dem gleichen ohmschen Widerstand genau die gleiche Leistung umsetzt, wie
im Mittel durch die Wechselspannung umgesetzt wird.
Anders ausgedrückt:
Man bestimmt die mittlere Leistung der Wechselspannung und sucht dann die
Gleichspannung, welche die gleiche Leistung erzeugt. Diese Gleichspannung
entspricht dann dem Effektivwert der Wechselspannung.
Genau wie Gleichspannungen werden Effektivwerte von Wechselspannungen mit
einem großen Buchstaben gekennzeichnet. Der Effektivwert einer Wechselspannung
u(t) erhält also den Großbuchstaben U.
Knotenregel (1. Kirchhoff Regel)
Beginnen wir mit der Knotenregel, oftmals auch als erste Kirchhoff Regel bezeichnet.
Die Aussage hinter dieser ist eigentlich recht einfach: Der Strom, der in einen
Knoten fließt, muss genauso groß sein, wie der Strom, der raus fließt. Schaut
euch erst einmal die folgende Grafik an, darunter findet ihr Erklärungen dazu.
Die Pfeile die auf den Knoten hinzeigen bedeuten: Der Strom fließt in den Knoten.
Die Pfeile vom Knoten weg sagen: Der Strom fließt raus aus dem Knoten. Die
Knotenregel besagt, dass die Ströme die reinfließen so groß sind, wie die Ströme,
die rausfließen. Dies bedeutet für unser Beispiel:

I1 + I 2 + I 4 = I 3
Die Summe der eingehen Ströme ist gleich groß wie die Summe der
ausgehenden Ströme. Kennt man in unserem Beispiel drei der vier Ströme, kann
man die vierte berechnen.
Maschenregel (2. Kirchhoff Regel)
Die 2. Kirchhoff Regel wird auch als Maschenregel bezeichnet. Mit ihr lassen sich
Angaben zur Spannung in einer Masche machen. Auch hierzu nehmen wir ein
einfaches Beispiel, um den Sachverhalt möglichst einfach zu erläutern. Schaut euch
dazu erst einmal die folgende Grafik an:
Wir haben in unserem Beispiel eine Spannungsquelle und drei Widerstände. Die
Maschenregel besagt, dass die Spannung aus der Quelle genauso groß ist, wie die
Spannung, die an den drei Widerständen abfällt. Dies sieht dann wie folgt aus:

USpannungsquelle = UWiderstand 1 + UWiderstand 2 + UWiderstand 3