Kapitel 8 Anwendung des Lagrangre

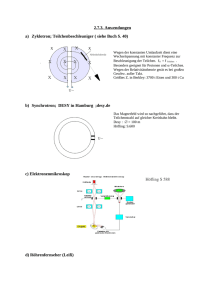
Kapitel 8
Anwendung des
Lagrangre-Formalismus
8.1
Eindeutigkeit der Lagrange-Funktion
Die Lagrange-Funktion, die nach dem Hamiltonschen Prinzip die Bewegung eines
Systems charakterisiert, ist offenbar unbestimmt bezüglich der Addition eines
konstanten Faktors: Addiert man eine Konstante a zur Lagrange-Funktion, dann
erhöht sich die Wirkung S in Gleichung (7.29) um den konstanten Wert (t2 −
t1 )a, völlig unabhängig von der durchlaufenen Bahnkurve. Darüberhinaus ist die
Lagrange-Funktion auch unbestimmt gegenüber der Addition einer beliebigen
Funktion F (q, q̇, t), die sich als totale Ableitung nach der Zeit einer Funktion
f (q, t) schreiben läßt, die von den Koordinaten und von der Zeit, nicht aber von
den Geschwindigkeiten abhängt:
F (q, q̇, t) =
d
f (q, t).
dt
Denn das bestimmte Integral von F liefert einen Beitrag
 t2
 t2
d
F (q, q̇, t) dt =
f (q, t) dt
t1
t1 dt
= f (q(t2 ), t2 ) − f (q(t1 ), t1 ) ,
(8.1)
(8.2)
der nur von den Randpunkten abhängt, sonst aber völlig unabhängig von der
durchlaufenen Bahn ist.
Ein Beispiel für eine solche Funktion ist F = aq̇, wobei a eine Konstante ist.
Das heißt jedoch nicht, daß es keine geschwindigkeitsabhängigen Potentiale gibt.
Die Lagrangefunktion eines Elektrons in elektrischen und magnetischen Feldern
läßt sich beispielsweise wie folgt schreiben:
L=
m 2
v − e(φ − v · A).
2
65
(8.3)
Auch wenn das Vektorpotential A nicht von der Zeit abhängt, wenn also gilt
∂A
= 0,
∂t
(8.4)
läßt sich der Ausdruck v · A im Allgemeinen trotzdem nicht als totale Ableitung
nach der Zeit einer Funktion f (q, t) schreiben, denn die totale Ableitung des
Vektorpotentials nach der Zeit,
dA
∂A ∂A ∂x ∂A ∂y ∂A ∂z
=
+
+
+
,
dt
∂t
∂x ∂t
∂y ∂t
∂z ∂t
(8.5)
kann trotzdem von Null verschieden sein, wenn das Vektorpotential A räumlich
nicht konstant ist.
Dagegen läßt sich die Funktion F = q̇ 2 nicht als totale Ableitung der Zeit einer
Funktion f (q, t) schreiben. Wir können also nicht ohne weiteres einen Ausdruck,
der proportional zur kinetischen Energie ist, zur Lagrangefunktion hinzufügen,
ohne daß sich die resultierende Bahnkurve ändert.
Wegen der Homogenität und der Isotropie des Raumes muß die Lagrangefunktion invariant unter einer Translation oder Rotation des Koordinatensystems sein.
Die Lagrangefunktion darf also nicht explizit von der Zeit oder den Koordinaten
oder von der Richtung der Geschwindigkeiten abhängen. Wir könnten die Lagrangefunktion daher als Funktion des Betrages der Geschwindigkeit schreiben.
üblich, und völlig äquivalent, ist es, eine Lagrangefunktion L(q̇ 2 ) in Abhängigkeit
des Quadrats der Geschwindigkeit zu formulieren.
8.2
Das freie nicht-relativistische Teilchen
Wir versuchen im Folgenden, aus grundlegenden Annahmen die LagrangeFunktion für ein freies Teilchen zu bestimmen und allgemeine Aussagen für die
Lagrange-Funktion eines Systems wechselwirkender Teilchen zu gewinnen. Wir
beschränken uns zunächst auf Teilchen mit niedrigen Geschwindigkeiten, so daß
wir die Galilei-Transformation verwenden können, und behandeln danach relativistische Teilchen, die die Lorentz-Transformation erfordern.
Betrachten wir ein freies Teilchen in einem Inertialsystem S. Dabei soll ein
Inertialsystem ein Bezugssystem sein, das homogen bezüglich Raum und Zeit und
isotrop bezüglich des Raumes sein. Das heißt, eine Verschiebung oder eine Drehung der Koordinatenachsen im Raum soll die Bewegungsgleichung nicht ändern.
Das Gleiche soll für eine Verschiebung der Zeitachse und für eine Transformation
in ein gegenüber dem ursprünglichen Koordinatensystem gleichförmig bewegtes
Koordinatensystem gelten.
Aus der Homegenität des Raumes folgern wir, dass die Lagrange-Funktion L
nicht vom Ort r des Teilchens abhängen darf, da sonst eine Verschiebung des
Koordinatensystems zu einer anderen Bewegungsgleichung des Teilchens ändern
66
würde. Aus der Isotropie des Raumes folgt, dass L nicht von der Richtung der
Geschwindigkeit abhängen darf, da die Bewegungsgleichung sich andernfalls bei
einer Drehung des Koordinatensystems ändern würde.
Die Lagrange-Funktion für ein freies Teilchen muss sich daher als Funktion des
Quadrats des Geschwindigkeitsvektors schreiben lassen. Als Ansatz verwenden
wir eine zunächst unbekannte Funktion F (w) mit w = v2 und schreiben
L(v) = F (w)
(8.6)
Nach dem Galileischen Relativitätsprinzip müssen wir zur gleichen Bewegungsgleichung gelangen, wenn wir das Teilchen aus einem zweiten Inertialsystem S’
beobachten, das gegenüber dem ersten mit der konstanten Geschwindigkeit du bewegt ist, die wir hier infinitesimal klein wählen wollen. Die Lagrange-Funktionen
im in den Systemen S und S’ dürfen sich deshalb, wie oben gezeigt, höchstens
um die totale Ableitung einer Funktion f (r), die nur vom Ort r abhängt, unterscheiden:
∂f
d
·v.
(8.7)
L(v − du) = L(v) + f (r) = L(v) +
dt
∂r
Da wir die Relativgeschwindigkeit du hier infinitesimal klein gewählt haben,
können wir mit (8.6) die Lagrange-Funktionen im System S’ auch in der Form
L(v − du) = L(v) +
∂F
∂F ∂w
· du = L(v) +
2v · du .
∂w ∂v
∂w
(8.8)
Daraus folgt
∂f
∂F
2v · du =
·v.
(8.9)
∂w
∂r
Da die vorstehende Gleichung für beliebige Geschwindigkeiten v gelten muss,
folgt:
∂f
∂F
2du =
.
(8.10)
∂w
∂r
Da in dieser Gleichung die Variable w nur im Faktor ∂F/∂w auftritt, muss F
eine lineare Funktion in w sein:
F (w) = αw + β .
(8.11)
Da konstante Terme in der Lagrange-Funktion unerheblich sind, wählen wir β =
0. Der konstante Faktor α bleibt vorerst unbestimmt, denn im Falle freier Teilchen
kann er beliebig gewählt werden, da aus der Lagrange-Funktion
L(v) = αv2
(8.12)
unabhängig von der Wahl des Faktors α immer die Bewegungsgleichung
 
d ∂L
dv
= 2α
=0,
(8.13)
dt ∂v
dt
67
also
v = const.
(8.14)
folgt.
Betrachten wir nun zwei freie, nicht miteinander wechselwirkende Teilchen,
die durch die Lagrange-Funktionen L1 und L2 beschrieben werden sollen. Eine
Lagrange-Funktion L für das Gesamtsystem, das aus diesen beiden freien Teilchen
besteht, hat in voller Allgemeinheit die Form
L(v1 , v2 ) = L1 (v1 ) + L2 (v2 ) + L1,2 (v1 , v2 ) .
(8.15)
Partielle Ableitung nach v1 und nachfolgende totale Ableitung nach der Zeit
liefert






d ∂L1
d ∂L1,2
d ∂L
=
+
.
(8.16)
dt ∂v1
dt ∂v1
dt ∂v1
Nun wird die Bewegungsgleichung des ersten Teilchens, die ja nach Voraussetzung
nicht vom zweiten Teilchen abhängig sein soll, schon vollständig durch den ersten
Summanden auf der rechten Seite von Gleichung (8.16) beschrieben. Die Funktion L1,2 (v1 , v2 ) muss also dergestalt sein, dass sie nichts zur Bewegungsgleichung
des ersten Teilchens beiträgt. Für das zweite Teilchen können wir genauso argumentieren, so dass wir die Funktion L1,2 weglassen und die Lagrange-Funktion
des Gesamtsystems in der Form
L(v1 , v2 ) = L1 (v1 ) + L2 (v2 )
(8.17)
schreiben können. Wenn wir statt zwei freien, nicht wechselwirkenden Teilchen
viele solcher Teilchen betrachten, können wir ähnlich vorgehen. Allgemein können
wir daher die Lagrange-Funktion eines Systems von N nicht wechselwirkenden
Teilchen als Summe der N Lagrange-Funktionen für einzelne freie Teilchen schreiben:
2
L(v1 , v2 , . . . , vN ) = α1 v12 + α2 v22 + . . . + αN vN
.
(8.18)
Im Falle eines Systems von Teilchen, die miteinander wechselwirken, müssen
wir die Lagrange-Funktion (8.18) um einen Term ergänzen, der diese Wechselwirkung berücksichtigt. Die Erfahrung lehrt, dass sich in der Mechanik alle Wechselwirkungen zwischen zwei Teilchen durch eine Funktion beschreiben lassen, die
ausschließlich vom Abstand zwischen den beiden Teilchen abhängt. Die LagrangeFunktion lautet dann
L(v1 , v2 , . . . , vN ) =
N

αi vi2 −
i=1

Ui,j (|ri − rj |) .
(8.19)
i,j
Offenbar gilt
∂Ui,j
∂Ui,j
=−
,
∂ri
∂rj
68
(8.20)
eine Aussage, die äquivalent zum dritten Newtonschen Gesetz ist. Im Falle von
wechselwirkenden Teilchen sind die konstanten Faktoren αi nicht mehr beliebig,
denn wir erhalten die Bewegungsgleichungen
dv
1  ∂(Ui,j + Uj,i )
=
.
(8.21)
dt
2αi j
∂ri
Die Funktionen Ui,j geteilt durch den Faktor αi legen eine Eigenschaft des Teilchens i fest, nämlich wie stark das Teilchen durch Wechselwirkungen mit anderen
Teilchen beschleunigt wird. Wir können also nicht über die Ui,j und über die αi
gleichzeitig frei verfügen. Sobald wir etwa α1 willkürlich bestimmt haben, sind alle
U1,j und damit wiederum alle übrigen αi festgelegt. Um zur gleichen Schreibweise
wie in der Newtonschen Mechanik zu kommen, wählen wir speziell α = m/2,
wobei m die Masse ist, die durch einen Prototypen festgelegt werden muss. Die
Lagrange-Funktion für ein System von Teilchen lautet damit
L(v1 , v2 , . . . , vN ) =
N

mi
i=1
8.3
2
vi2 −

Ui,j (|ri − rj |) .
(8.22)
i,j
Das relativistische freie Teilchen
Die Bewegungsgleichungen
d
dτ

∂L
∂uµ

−
∂L
=0
∂xµ
(8.23)
sollen invariant unter Lorentz-Transformationen sein. Man kann zeigen, dass dann
auch die Lagrange-Funktion L Lorentz-invariant sein muss. Außerdem hängt L
aufgrund der Homogenität des Raumes und der Zeit nicht von xµ ab. Aufgrund
der Lorentz-Invarianz von L und der Isotropie des Raumes kann L auch nicht
von den einzelnen Komponenten der Vierergeschwindigkeit abhängen, sondern
nur vom Betrag uµ uµ .
Als Ansatz für die Lagrange-Funktion verwenden wir eine noch unbekannte
Funktion f (z) und schreiben
L = f (z) mit z = uµ uµ = gµν uµ uν .
(8.24)
Für die partiellen Ableitungen erhalten wir
∂L
∂f ∂z
=
= 2f ′ uµ .
µ
∂u
∂z ∂uµ
(8.25)
Hier ist f ′ , die Ableitung von f nach z an der Stelle z = uµ uν , eine Konstante,
da auch uµ uµ eine Konstante ist. Aus der Lagrange-Gleichung folgt jetzt


d
∂L
duµ
= 2f ′
=0.
(8.26)
µ
dτ ∂u
dτ
69
Die Bewegungsgleichung eines freien, relativistischen Teilchens lautet daher
duµ
=0.
dτ
(8.27)
Welche Funktion f wir wählen spielt offenbar für die Bewegungsgleichung des freien Teilchens keine Rolle. Eine spezielle Wahl für f bestimmt nur den konstanten
Faktor f ′ , der keinen Einfluss auf die Bewegungsgleichung hat. Wir verwenden
im Folgenden die Funktion
1
(8.28)
f (z) = mz ,
2
wobei m die Ruhemasse des Teilchens ist. Die Lagrange-Funktion des freien,
relativistischen Teilchens lautet dann
1
L = muµ uν .
2
(8.29)
Wir definieren den Viererimpuls
pµ = muµ
(8.30)
und schreiben die Bewegungsgleichung in der Form
dpµ
=0.
dτ
8.4
(8.31)
Minkowski-Kraft
Für ein Teilchen, das mit seiner Umgebung wechselwirkt, schreiben wir die
Lagrange-Funktion in der Form
1
L = muµ uν − V ,
2
(8.32)
wobei V eine orts- und zeitabhängige Funktion ist, die wir als Potential bezeichnen. Wir setzen diese Lagrange-Funktion in die Lagrange-Gleichung (8.23) ein
und erhalten die Bewegungsgleichungen
dpµ
∂V
=
.
dτ
∂xµ
(8.33)
Wir bezeichnen die vier partiellen Ableitungen des Potentials als Vierer- oder
Minkowski-Kraft
∂V
Fµ =
.
(8.34)
∂xµ
Die Bewegungsgleichungen (8.33) können wir mit Hilfe der Minkowskikraft auch
in der Form
dpµ
µ
F =
(8.35)
dτ
70
schreiben.
Als Beispiel betrachten wir ein Teilchen mit der Ruhemasse m, auf das in
seinem Ruhesystem eine konstante Kraft mit dem Betrag f = ma in positive
x-Richtung wirkt. Der Einfachheit halber sei die Bewegung des Teilchens auf die
x-Achse beschränkt. Wir betrachten das Teilchen im System S, in dem es sich
zur Zeit t = 0 am Ort x(0) = 0 befindet und die Geschwindigkeit v(0) = 0
hat. Zu einem willkürlich gewählten Zeitpunkt sei das System S’, das sich mit v
gegen S bewegt, das Ruhesystem des Teilchens. In S’ lautet die Viererkraft nach
Voraussetzung
F′ = (0, ma, 0, 0) .
(8.36)
Mit Hilfe der Lorentz-Transformation erhalten wir aus F′ die Viererkraft in S:
F = (γvma/c, γma, 0, 0) .
(8.37)
Wir können jetzt die vom Koordinatensystem unabhängige Bewegungsgleichung
F1 =
dp1
dτ
(8.38)
speziell für das System S formulieren. Für die x-Komponente erhalten wir so
γma =
dp1
d
= γ (γmv)
dτ
dt
(8.39)
oder
d
(γmv) .
(8.40)
dt
Die Vereinfachung dieser Bewegungsgleichung mit Hilfe der dynamischen Masse
m̃ = γm zu
d
(m̃v)
(8.41)
f=
dt
ist nur für den Fall gültig, daß Kraft und Bewegung parallel zueinander stehen
und wird hier nicht weiter verwendet. Die Lösung dieser Bewegungsgleichung ist
aufwendig, so daß hier nur das Ergebnis
c
v(t) =  
(8.42)
c 2
+1
at
f = ma =
und
x(t) = ct


c 2
c
+1−
at
at

(8.43)
angegeben werden soll. Die Richtigkeit dieser Lösung läßt sich durch Einsetzen
in (8.40) überprüfen. Zu Beginn der Bewegung ist γ ≈ 1 und t ≪ c/f und wir
erhalten das zweite Newtonsche Gesetz
f =m
71
dv
dt
(8.44)
mit den bekannten Lösungen
v(t) = at
(8.45)
und
1
x(t) = at2 .
(8.46)
2
Mit zunehmender Zeit nähert sich die Geschwindigkeit v asymptotisch der Lichtgeschwindigkeit. Die Beschleunigung ist aus der Sicht von S jedoch nicht konstant,
sondern strebt gegen Null. Wenn die Ruhemasse Null ist, bewegt sich das Teilchen
stets mit Lichtgeschwindigkeit und die Bahnkurve ist durch x(t) = ct gegeben.
8.5
Lagrangesche Multiplikatoren
Die Methode der Lagrangeschen Multiplikatoren dient zum Auffinden von Extremwerten unter Nebenbedingungen. Der Anschaulichkeit wegen betrachten wir
zunächst eine Funktion f (x, y), die von zwei Variablen x und y abhängt, und unter der Nebenbedingung g(x, y) = 0 maximiert werden soll. In diesem Fall können
wir uns die Menge aller Punkte (x, y), die die Nebenbedingung g = 0 erfüllen, als
Kurve in der x − y−Ebene vorstellen (rote Linie in Abb. 8.1).
Abbildung 8.1: Methode
www.wikipedia.de]
der
Lagrangeschen
Multiplikatoren
[Quelle:
Im allgemeinen Fall, wo die Funktion f von n Variablen abhängt, und k
unabhängige Nebenbedingungen erfüllt werden müssen, wird durch die Nebenbedingungen eine k-dimensionale Hyperfläche im n-dimensionalen Vektorraum
definiert.
Der Gradient


∂g
∂g/∂x
=
(8.47)
∂g/∂y
∂r
(rote Pfeile in Abb. 8.1) steht stets senkrecht auf der durch g festgelegten Kurve.
Wir können uns diese Tatsache wie folgt klarmachen: Sei r0 = (x0 , y0 ) ein Punkt
72
der die Nebenbedingung g = 0 erfüllt und r0 + dr0 ein benachbarter Punkt der
durch die infinitesimale Verschiebung dr0 = (dx, dy) aus r0 hervorgeht. Es gilt
dann
∂g
g(x0 + dx, y0 + dy) =
· dr ,
(8.48)
∂r
wobei der Gradient von g an der Stelle r0 ausgewertet wird. Wenn auch
(x0 + dx, y0 + dy) die Nebenbedingung g = 0 erfüllt, dann ist der Vektor dr tangential zur durch die Nebenbedingung festgelegten Kurve, und außerdem muss
die linke Seite von (8.48) verschwinden. Daher muss auch das Skalarprodukt auf
der rechten Seite von (8.48) Null sein, so dass der Gradient von g senkrecht auf
der Kurve stehen muss.
Nehmen wir nun zusätzlich an, r0 sei das gesuchte Extremum von f unter
der Nebenbedingung g = 0. Dann können wir den Funktionswert von f in einem
benachbarten Punkt r0 + dr0 , der ebenfalls die Nebenbedingung g = 0 erfüllt, in
der Form
∂f
· dr
(8.49)
f (x0 + dx, y0 + dy) = f (x0 , y0 ) +
∂r
schreiben. Da f am Punkt r0 extremal sein soll muss f (x0 , y0 ) = f (x0 +dx, y0 +dy)
und damit
∂f
· dr = 0
(8.50)
∂r
sein. Da dr wie schon gesagt tangential zur Kurve ist, muss daher im Punkt r0
auch der Gradient von f senkrecht auf der Kurve stehen. Der Gradient von f
muss also ein Vielfaches des Gradienten von g sein:
∂f
∂g
+λ
=0
∂r
∂r
(8.51)
Dabei ist λ ein zunächst unbekannter Parameter.
Wir können Gleichung (8.51) auch so interpretieren, dass eine notwendige
Bedingung für das Vorliegen eines Extremums, das die Nebenbedingung erfüllt,
ist, dass der Gradient der Funktion
h = f + λg
(8.52)
verschwindet. Um das Extremum tatsächlich zu bestimmen muss noch der Parameter λ aus Gleichung (8.51) mit Hilfe der Nebenbedingung g = 0 eliminiert
werden.
Dieses Verfahren ist häufig vorteilhaft, gegenüber der alternativen Methode,
mit Hilfe der Nebenbedingung eine der Variablen x oder y zu eliminieren, so dass
f nur noch als Funktion einer Variablen vorliegt, und anschließend das Extremum
von f (y) beziehungsweise f (x) zu suchen.
Die Methode der Lagrangeschen Multiplikatoren lässt sich auch auf die
Aufstellung der Lagrange-Funktion anwenden, wenn nicht alle Koordinaten unabhängig sind, weil beispielsweise Nebenbedingungen vorliegen. Wenn
73
L(q1 , . . . , qn ) die Lagrange-Funktion für den Fall ist, dass alle Koordinaten qi
unabhängig sind, dann kann die Lagrange-Funktion L′ (q1 , . . . , qn ) für den Fall
einer Nebenbedingung g(q1 , . . . , qn ) = 0 in der Form
L′ (q1 , . . . , qn ) = L(q1 , . . . , qn ) + λg(q1 , . . . , qn )
(8.53)
geschrieben werden.
8.6
Lagrange-Dichte
Besteht ein System nicht aus einer endlichen Anzahl von Teilchen sondern aus
einem Kontinuum, müssen wir statt einer Langrange-Funktion eine LagrangeDichte formulieren. Wir machen uns dies am Beispiel einer schwingenden Saite
klar.
Zunächst fassen wir die Saite als Kette der Länge ℓ auf, die aus N diskreten
Massenpunkten besteht, die auf der x-Achse in Abständen von ∆x = ℓ/(N − 1)
angeordnet sind und durch Federn miteinander verbunden sind. Die Federkonstante sei D, was einem Elastizitätsmodul der Federn von E = D∆x entspricht.
Wir nehmen der Einfachheit halber an, dass die Federn eine Ruhelänge von Null
haben. Andernfalls bekommen wir, zumindest für stärkere Schwingungen der Kette, ein nichtlineares Verhalten. Die Gesamtmasse der Kette beträgt M , so dass
jeder einzelne Massenpunkt die Masse m = M/N besitzt.
Im Gleichgewicht befinden sich alle Massenpunkte genau auf der x-Achse, jeder einzelne Massenpunkt kann jedoch in Richtung der y-Achse ausgelenkt werden. Wir numerieren die Massenpunkte mit dem Index i und bezeichnen die
Auslenkungen der Massenpunkte mit yi . Nach dem Hookeschen Gesetz hat eine
Feder die potentielle Energie Du2 /2, wenn u ihre Auslenkung aus der Ruhelage
ist. Im Gleichgewicht, wenn alle yi Null sind, hat die Kette daher die potentielle
Energie
N
−1

1
D∆x2
(8.54)
2
i=1
Für beliebige Auslenkungen yi hat die Feder zwischen den Massenpunkten i und
i + 1 die Länge

∆x2 + (yi+1 − yi )2
(8.55)
und die potentielle Energie der Kette lautet dann
N
−1

i=1

1  2
D ∆x + (yi+1 − yi )2
2
(8.56)
Da nur die Änderungen der potentiellen Energie, nicht aber deren absoluter Wert
für die Bewegungsgleichung von Bedeutung sind, können wir die potentielle Energie um einen willkürlichen Betrag verschieben und für die potentielle Energie der
74
Abbildung 8.2: Schwingende Saite.
Kette den Ausdruck
N −1
N −1 
1 
1 
(yi+1 − yi )2 = E
U= D
2 i=1
2 i=1
yi+1 − yi
∆x
2
∆x
(8.57)
verwenden.
Die kinetische Energie der Kette ist
T =
N

1
i=1
2
mẏi2
(8.58)
Wir führen jetzt die Liniendichte der Masse
ρ=
M
m N
=
ℓ
∆x N − 1
(8.59)
ein und schreiben die kinetische Energie in der Form
T =
N

1
i=1
2
ρ∆x
N −1 2
ẏi
N
(8.60)
Die Lagrange-Funktion der Kette lautet dann
N −1 
N
1 N −1 2
1 
L=T −U = ρ
ẏi ∆x − E
2
N i=1
2 i=1
yi+1 − yi
∆x
2
∆x
(8.61)
Wir führen jetzt den Grenzübergang N → ∞ durch, um von der Kette aus endlich vielen diskreten Massenpunkten zu einer kontinuierlichen Saite überzugehen.
Dabei ersetzen wir die Summen durch ein Integrale über x und der Differenzenquotient im Ausdruck für die potentielle Energie wird durch die Ableitung der
Funktion y(x, t) nach x ersetzt:
 x2
 x2
1
1
2
L= ρ
ẏi dx − E
y ′2 dx
(8.62)
2 x1
2
x1
75
Wir wollen die Lagrange-Funktion jetzt als Integral über eine Lagrange-Dichte L
schreiben:
 x2
L dx
(8.63)
L=
x1
Der Vergleich von (8.62) und (8.63) zeigt, dass wir die Lagrange-Dichte in der
Form
1
1
L = ρẏ 2 − Ey ′2
(8.64)
2
2
schreiben müssen. Für die Wirkung der Saite gilt dann
 t2  x2
L(y) dx dy
(8.65)
S[y] =
x1
t1
Gesucht ist jetzt also eine Funktion y(x, t), für die die Wirkung S[y] extremal
wird. In Analogie zu den Lagrange-Gleichungen 2. Art schreiben wir als Bedingung
 


d ∂L
d ∂L
∂L
=0
(8.66)
+
−
′
dt ∂ ẏ
dx ∂y
∂y
Im Unterschied zur Herleitung in Abschnitt 7.7 müssen wir die Lagrange-Dichte
auch nach y ′ partiell ableiten, da die Lagrange-Dichte im Allgemeinen explizit
von y ′ abhängt. Zwar ist y ′ festgelegt, wenn y(x) für alle x bekannt ist, aber es
reicht nicht aus, nur y zu varieren. Die partielle Ableitung von L sagt ja nur
etwas darüber aus, wie sich L ändert, wenn wir y an der Stelle x variieren und
alle anderen Variablen von L konstant bleiben, also auch y ′ .
Wir wollen Gleichung (8.66) jetzt auf die Lagrange-Dichte der Saite anwenden.
Wir erhalten dann
d
d
(ρẏ) −
(Ey ′ ) = ρÿ − Ey ′′ = 0
dt
dx
Wenn wir

c=
E
ρ
(8.67)
(8.68)
als Wellengeschwindigkeit der Saite definieren, dann erhalten wir die Wellengleichung der schwingenden Saite in ihrer üblichen Form:
y ′′ −
8.7
1
ÿ = 0
c2
(8.69)
Zeitunabhängige Schrödinger-Gleichung
Wir betrachten in einem eindimensionalen Raum ein mikroskopisches Teilchen,
das durch die reelle Wellenfunktion ψ(x) beschrieben wird. Ohne weitere Begründung gehen wir davon aus, dass die kinetische Energie des Teilchens durch
76
den Ausdruck

+∞
−∞
1
2
(h̄ψ ′ ) dx
2m
beschrieben wird.1 Für die potentielle Energie schreiben wir
 +∞
V (x) (ψ)2 dx ,
(8.70)
(8.71)
−∞
wobei V (x) ein klassisches Potential ist. Wir können jetzt die Lagrange-Funktion
des Teilchens in der Form
 +∞
 +∞
 + inf
1
′
′ 2
2
L(ψ, ψ ) =
(h̄ψ ) dx −
V (x)ψ dx + λ
ψ 2 dx
(8.72)
2m
−∞
−∞
−∞

schreiben. Wir haben hier die Nebenbedingung ψ 2 dx = 1, dass nämlich die
Wahrscheinlichkeit, das Teilchen irgendwo zu finden, eins sein muss, mit einem
Lagrangeschen Multliplikator λ zur Lagrange-Funktion addiert. Wir können die
Lagrange-Funktion auch analog zu Gleichung (8.63) durch die Lagrange-Dichte
L=
1
2
(h̄ψ ′ ) − V (x)ψ 2 + λψ 2
2m
(8.73)
ausdrücken. Wenn wir diese Lagrange-Dichte in die Lagrange-Gleichung (8.66)
einsetzen, erhalten wir die sogenannte zeitunabhängige Schrödinger-Gleichung
 2

h̄
+ V (x) ψ = Eψ
(8.74)
2m
als Bewegungsgleichung für die Wellenfunktion ψ. Wir haben der Konvention
wegen im letzten Schritt statt λ das E als Symbol für den Langrangeschen Multiplikator verwendet.
8.8
Zusammenfassung
Aus der Lagrange-Funktion kann man mit Hilfe der Lagrange-Gleichung die Bewegungsgleichung und damit bei gegebenen Randbedingungen die Bahnkurve für
ein System erhalten. Umgekehrt kann man allerdings nicht aus der Bahnkurve
eine eindeutig festgelegte Lagrange-Funktion erhalten. Verschiedene LagrangeFunktionen können zur gleichen Bewegungsgleichung führen. Die Addition eines
konstanten Terms zur Lagrange-Funktion oder die Multiplikation mit einem konstanten Faktor ändern die resultierende Bewegungsgleichung nicht. Darüber hinaus darf zur Lagrange-Funktion ein beliebiger Ausdruck addiert werden, sofern
1
Eine Motivation für diese Annahme findet sich in Abschnitt 7.2. Ansonsten muss auf Darstellungen der Quantenmechanik verwiesen werden.
77
sich dieser als zeitliche Ableitung einer Funktion schreiben lässt, die nur von Ort
und Zeit abhängt.
Symmetriebetrachtungen legen nahe, dass wir die Lagrange-Funktion eines
freien, nichtrelativistischen Teilchens in der Form L = mv2 /2 schreiben können,
während das relativistische Teilchen durch L = muν uν /2 beschrieben wird. Beschreibt man die Wechselwirkung eines Teilchens mit seiner Umgebung durch ein
Potential V , dann lautet die relativistische Lagrange-Funktion L = muν uν /2−V .
Führt man die Vierervektoren F µ und pµ ein, die als Minkowski-Kraft beziehungsweise als Viererimpuls bezeichnet werden, dann erhält man mit Hilfe der
Lagrange-Gleichung die Bewegungsgleichung
Fµ =
dpµ
,
dτ
(8.75)
die in Analogie zum zweiten Newtonschen Gesetz formuliert ist.
Der Lagrange-Formalismus für diskrete Teilchen lässt sich auf kontinuierliche
Systeme ausweiten, indem man die Lagrange-Dichte L definiert. So lässt sich beispielsweise die Schwingung einer Saite behandeln oder die Schrödinger-Gleichung
als Bewegungsgleichung für eine Wellenfunktion verstehen.
78