Mathematik Matura BRP, Sommer 2016

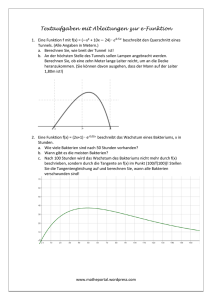
TEILPRÜFUNG ZUR BERUFSREIFEPRÜFUNG
Themenstellung für die
schriftliche Berufsreifeprüfung
aus dem Fach Mathematik und angewandte Mathematik
Termin: Sommer 2016
Prüfer:
Mag. Wolfgang BODISCH
Mag. Wolfgang GALSTERER
MMag. Stephan STRASSER
Punkteverteilung/Gewichtung:
Beispiel 1:
Beispiel 2:
Beispiel 3:
Beispiel 4:
Beispiel 5:
Beispiel 6:
Gesamt:
8
6
8
7
5
6
Punkte
Punkte
Punkte
Punkte
Punkte
Punkte
40 Punkte
Notenschlüssel:
40-37 Punkte
36-31 Punkte
30-25 Punkte
24-20 Punkte
19- 0 Punkte
Sehr gut
Gut
Befriedigend
Genügend
Nicht genügend
Seite 1
1. LINEARE UND RATIONALE FUNKTIONEN (8 P)
a) Im Supermarkt kostet 1 Kilogramm (kg) Biokarotten 2 €. Kauft man die
Karotten beim Gemüsebauern, so beträgt der Preis pro kg zwar 30 Cent
weniger, es kostet aber 10 € um zum Gemüsebauern zu fahren.
i)
Beschreiben Sie den zu bezahlenden Gesamtpreis P (in €) in Abhängigkeit
der gekauften Menge x (in kg) durch 2 lineare Funktionen PS und PG.
ii)
[2P]
Ermitteln Sie, wie viele Kilogramm Karotten man beim Gemüsebauern
mindestens kaufen müsste, damit sich die Fahrt lohnt.
[1P]
b) Der Gemüsebauer rechnet für die Produktion von Biokarotten mit 2000 €
Fixkosten und Produktionskosten von 1,3 € pro Kilogramm (kg).
i)
Ermitteln Sie, die Gesamtproduktionskosten K des Gemüsebauern als
lineare Funktion der Produktionsmenge x (in kg) und bestimmen Sie daraus
die Stückkosten (Gesamtproduktionskosten pro kg) K ( x) bei einer
Produktionsmenge von x kg sowie 10 Tonnen.
ii)
[1P]
Geben Sie an, gegen welchen Funktionswert die Funktion K ( x)
bei immer größer werdender Produktionsmenge strebt.
[1P]
c) Geben Sie eine Formel für den zu erzielenden Gewinn G in Abhängigkeit der
Produktionsmenge x an, wenn der Bauer das Produkt zum oben in a) angegebenen Verkaufspreis (Preis pro kg) verkauft und ermitteln Sie daraus,
wie viele kg Biokarotten der Gemüsebauer produzieren und verkaufen muss,
um einen Gewinn von 500 € zu erwirtschaften.
[3P]
Seite 2
2. KURVENENUNTERSUCHUNG (6 P)
Beim Kugelstoßen kann die Flugbahn der Kugel näherungsweise durch eine
Funktion 2. Grades beschrieben werden.
Die folgende Funktionsgleichung beschreibt näherungsweise die Flugbahn der Kugel
h( x ) =
− 0,09 x 2 + 1,7 x + 1,8
h( x) … Höhe in Metern (m) an der Stelle x
x
… Horizontale Entfernung von der Abwurfstelle A in Metern (m), x ≥ 0
a) Berechnen Sie die Wurfweite dieses Wurfes auf 2 Nachkommastellen genau. [1 P]
b) Ermitteln Sie den höchsten Punkt H der Flugbahn der Kugel und bestimmen Sie,
wie weit dieser vom Abwurfpunkt A entfernt ist.
[2 P]
c) Erstellen Sie eine Formel zur Berechnung des Steigungswinkels α an einer
beliebigen Stelle x beim Aufsteigen α = ………….
[1 P]
d) Entscheiden Sie, ob die nachstehend angegebene Beziehung gilt und begründen
Sie Ihre Antwort.
Abstoßwinkel = - Aufprallwinkel
[2 P]
Seite 3
3. EXPONENTIELLES WACHSTUM, PROZENTRECHNUNG (8P)
Faschiertes Fleisch darf nur am Tag der Herstellung verkauft werden, da sich im
Fleisch enthaltene Bakterien rasch vermehren und beim Menschen zu Erkrankungen
führen können. Eine gekühlte Lagerung ist dabei unbedingt einzuhalten, weil sich die
Bakterien im Fleisch nahezu exponentiell vermehren.
Bei Raumtemperatur verdoppelt sich die Anzahl der Bakterien alle 20 Minuten.
a) Stellen Sie unter dieser Voraussetzung ein Wachstumsgesetz auf, das die
Anzahl der Bakterien N in Abhängigkeit der Zeit t (in min) angibt.
[2 P]
b) Berechnen Sie, unter der Annahme, dass a = 1,035265 bzw. λ = 0, 034657
beträgt, wann die Bakterien bei einem Anfangswert von 20 Bakterien auf 160
angestiegen sind.
[2 P]
c) Abgepacktes Faschiertes wird normalerweise in mehreren Fettstufen angeboten,
mit rund 12 % bei reinem Rindsfaschierten und bis zu 35 % Fett bei reinem
Schweinsfaschierten. Ein Kunde kauft ein gemischtes Faschiertes vom Rind und
vom Schwein im Verhältnis 2 : 3.
Berechnen Sie den Fettgehalt von 50 dag Faschiertem in Prozent.
[2 P]
Seite 4
d) Bei hohen Temperaturen vermehren sich die Bakterien besonders stark.
Gegeben ist ein Funktionsgraph, der eine Bakterienvermehrung in faschiertem
Fleisch bei etwa 40 °C darstellt.
[2 P]
Kreuzen Sie die beiden zutreffenden Aussagen an:
Laut abgebildeten Graphen fällt die Bakterienanzahl kontinuierlich
Nach 30 Minuten hat sich die Anzahl der Bakterien verachtfacht.
Zu Beginn waren keine Salmonellen vorhanden.
Die Anzahl der Bakterien verdreifacht sich alle 10 Minuten.
Die Bakterienanzahl wächst in 10 Minuten um 100%.
Seite 5
4. TRIGONOMETRIE, ZAHLEN UND MASSE (7 P)
Vielen Menschen bietet der Wörthersee neben Erholung auch die Möglichkeit
Heißluft-Ballonfahrten zu machen, bei denen man einen besonders spannenden und
schönen Ausblick aus dem Ballonkorb hat.
a) Von einem 2 m über der Wasseroberfläche liegenden Punkt sieht ein Beobachter
einen Heißluftballon unter einem Höhenwinkel von 48°, sein Spiegelbild im See
erscheint unter dem Tiefenwinkel 50°.
i)
Stellen Sie die Situation in einer Skizze dar.
(1)
ii)
Ermitteln Sie die Höhe des Ballons über der Wasseroberfläche.
(2)
iii) Berechnen Sie die Entfernung des Ballons vom Beobachter.
(1) [4 P]
b) Der Heißluftballon erreicht nach 7 Minuten senkrechtem Steigflug eine Höhe von
0,84 km. Ermitteln Sie die mittlere Steiggeschwindigkeit in m/s.
[1 P]
c) Die Dichte von Luft beträgt etwa 1,3 ⋅10−3 g/cm3 .
Berechnen Sie die Masse der Luft in kg in einem Heißluftballon, der ein Volumen
von 2800 m³ Luft beinhaltet.
[2 P]
Seite 6
5. INTEGRALTHEORIE (5 P)
Auf einem rechteckigen Grundstück soll ein Swimmingpool angelegt werden, der eine
spezielle Form besitzen soll. Die Begrenzungslinien dieses Swimmingpools können im
Wesentlichen durch die angegebenen Funktionen beschrieben werden (x und y in m).
𝑓𝑓: 𝑦𝑦 = 𝑥𝑥² − 6𝑥𝑥 + 10 und
𝑔𝑔: 𝑦𝑦 = 0,5𝑥𝑥³ − 7𝑥𝑥 2 + 32𝑥𝑥 − 38
Ein Architekt schätzt die Fläche des Pools auf ungefähr 21 m².
Seite 7
a) Betrachten Sie die obige Grafik.
i)
Zeigen Sie, dass der in der Grafik markierte Schnittpunkt A tatsächlich
Element beider Funktionsgraphen ist.
ii)
[1 P]
Erklären Sie, welche Bedeutung die beiden Schnittpunkte für das
Berechnen des Flächeninhalts zwischen den beiden Funktionen haben.
[1 P]
b) 1 cm³ Wasser enthält ungefähr 3,34 ∙ 1022 Wassermoleküle. Das Becken ist 1,5 m
hoch befüllt.
i)
Berechnen Sie das Volumen des Wassers unter Verwendung der
Schätzung des Architekten.
ii)
[1 P]
Berechnen Sie die ungefähre Anzahl der Wassermoleküle im Becken. [1 P]
c) Dokumentieren Sie die exakte Berechnung des Flächeninhalts des Pools.
[1 P]
Seite 8
6. STATISTIK UND WAHRSCHEINLICHKEITSTHEORIE (6 P)
Eine Stichprobe der, bei einer Section-Control gemessenen, Durchschnittsgeschwindigkeiten von zehn Fahrzeugen ist in der nachfolgenden Tabelle aufgelistet.
v in km/h 88
113
93
98
121
98
90
98
105
129
a) Bestimmen Sie den arithmetischen Mittelwert 𝑥𝑥̅ und die empirische
Standardabweichung s der Durchschnittsgeschwindigkeiten der Stichprobe.
[1 P]
b) Bestimmen Sie aus dem Boxplot der Stichprobe (Kastenschaubild) den Median
sowie das obere und untere Quartil.
Ermitteln Sie außerdem die Spannweite und beschriften Sie das BoxplotDiagramm mit den statistischen Parametern.
[2 P]
Seite 9
c) Die Erfahrung zeigt, dass die Wahrscheinlichkeit, ein zufällig ausgewähltes Fahrzeug
mit einer erhöhten Durchschnittsgeschwindigkeit zu erfassen, 14% beträgt.
i)
Berechnen Sie den Erwartungswert µ und die Standardabweichung σ der
Schnellfahrer unter fünfzig zufällig ausgewählten Fahrzeuglenkern.
ii)
[1 P]
Berechnen Sie mit Hilfe der Binomialverteilung die Wahrscheinlichkeit, dass
genau 5 Schnellfahrer unter den fünfzig ausgewählten sind.
[1 P]
iii) Berechnen Sie mit Hilfe der Binomialverteilung die Wahrscheinlichkeit, dass
mindestens 5 Schnellfahrer unter den fünfzig ausgewählten sind.
[1 P]
Seite 10