3 10 6 11 1 8 7 4 12 2 5 13 11 5 v1 v2 v3 v4 v5 v6 v7 v8 v9 9

1.Aufgabe: Minimal aufspannender Baum
6
v3
5
v2
11
v1
v4
11
7
9
4
5
10+10 Punkte
v9 8
v5
10
v8
12
v6
3
13 v7
2
1
v10
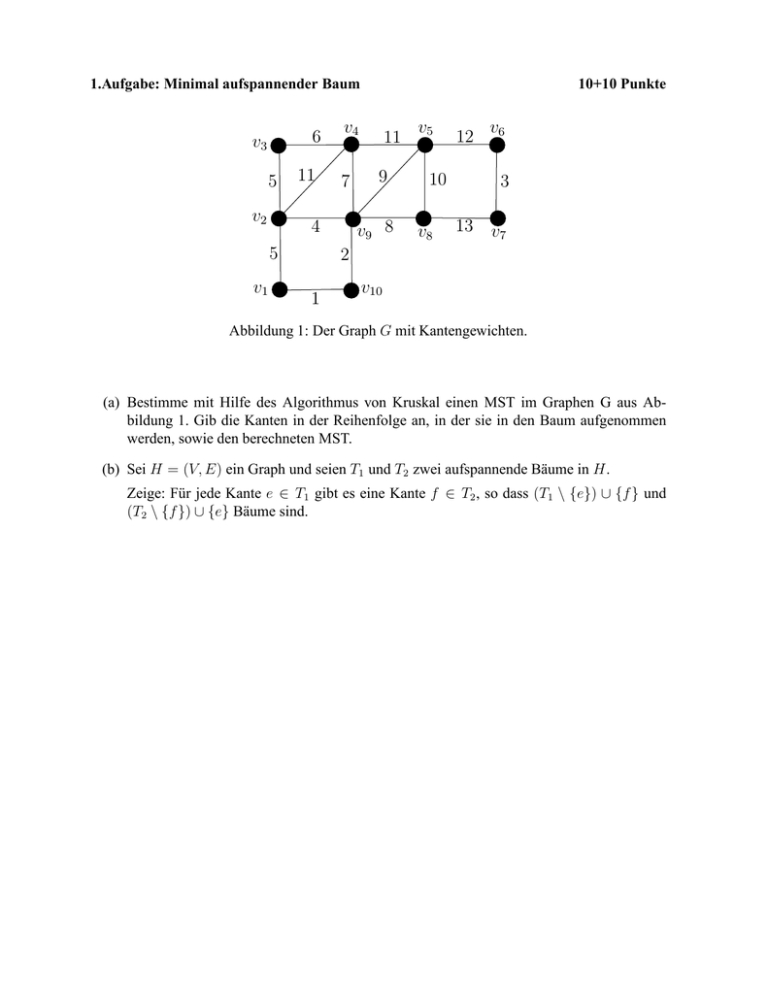
Abbildung 1: Der Graph G mit Kantengewichten.
(a) Bestimme mit Hilfe des Algorithmus von Kruskal einen MST im Graphen G aus Abbildung 1. Gib die Kanten in der Reihenfolge an, in der sie in den Baum aufgenommen
werden, sowie den berechneten MST.
(b) Sei H = (V, E) ein Graph und seien T1 und T2 zwei aufspannende Bäume in H.
Zeige: Für jede Kante e ∈ T1 gibt es eine Kante f ∈ T2 , so dass (T1 \ {e}) ∪ {f } und
(T2 \ {f }) ∪ {e} Bäume sind.
2.Aufgabe: Kürzester Weg
7+8 Punkte
v1
2
e1
2 e4 e3 8
v2
s
e2
6
1 e5
t
e6
4
v3
Abbildung 2: Der Graph G mit Kantenlängen.
(a) Bestimme im Graphen aus Abbildung 2 mit Hilfe des Algorithmus von Dijkstra einen
kürzesten Weg von s nach t. Gib für jeden Schleifendurchlauf die Längen und die Vorgänger,
die sich ändern, an.
(b) Sei H = (V, E) ein Graph und s und t zwei Knoten von H. Sei P ein kürzester s-t-Pfad
und v ein Knoten auf diesem Pfad. Sei Psv der Teilpfad von P , der in s startet und in v
endet. Zeige: Psv ist ein kürzester s-v-Pfad.
3.Aufgabe: Maximaler Fluss
s
1, 1
8, 7
3, 2
7+7+6 Punkte
v1 4, 4
3, 3
v2 5, 5
v3 2, 2
v4 7, 7
1, 1
t
3, 1
v5
Abbildung 3: Das Netzwerk (G, u, s, t). Die Tupel an den Kanten haben die Form (Kapazität,
Flusswert).
(a) Gib den Residualgraphen und die Residualkapazitäten zum Netzwerk (G, u, s, t) aus Abbildung 3 an.
(b) Führe eine Iteration des Algorithmus von Edmonds und Karp aus. Gib dazu den augmentierenden Pfad und das Netzwerk mit den neuen Flusswerten an.
(c) Ein Fluss kann auf Pfade und Kreise mit konstantem Fluss zerlegt werden. Gib, zu dem
Fluss aus Abbildung 3, einen s-t-Pfad mit konstantem Flusswert 1 und einen mit konstantem Flusswert 2 an.
4.Aufgabe: Matching in bipartiten Graphen
4+2+2+2+5 Punkte
v1
v5
v2
v6
v3
v7
v4
v8
Abbildung 4: Der bipartite Graph G.
Wir betrachten den bipartiten Graphen G aus Abbildung 4. Es soll mit Hilfe der Flussformulierung ein kardinalitätsmaximales Matching in G bestimmt werden.
(a) Zeichne das Netzwerk, in dem ein maximaler Fluss bestimmt werden muss.
(b) Trage einen Fluss mit Wert 3 in das Netzwerk ein.
(Hinweis: Dazu braucht kein Algorithmus angewendet zu werden.)
(c) Zeichne einen s-t-Cut der Größe 3 in das Netzwerk ein. Gib die Kanten an, die zum Cut
gehören.
(d) Gib ein minimales Vertex Cover für den Graphen G an.
(e) Sei H ein bipartiter Graph und H ′ das zugehörige Netzwerk zur Bestimmung eines kardinalitätsmaximalen Matchings in H mit Hilfe eines maximalen Flusses.
Beschreibe allgemein, wie man aus einem minimalen s-t-Cut in H ′ ein Vertex Cover für
H konstruieren kann.
Begründe dabei, warum die von dir beschriebene Methode immer funktioniert.
5.Aufgabe: Maximales Matching in allgemeinen Graphen
5+10 Punkte
v1
v12
v11
v5
v13
v2
v3
v14
v6
v16
v9
v17
v4
v7
v10
v15
v18
v8
Abbildung 5: Graph G.
(a) Finde ein kardinalitätsmaximales Matching im Graphen G aus Abbildung 5.
(Hinweis: Dazu braucht kein Algorithmus angewendet zu werden).
(b) Begründe, dass jedes Matching mindestens zwei Knoten aus G nicht enthält.
6.Aufgabe: Fragen
3+3+3+3+3 Punkte
(a) Vergleiche den Moore-Bellman-Ford-Algorithmus mit dem Algorithmus von Dijkstra.
Nenne einen Vorteil und einen Nachteil des ersten gegenüber dem zweiten.
(b) Wie lautet die Tutte-Berge-Formel?
(c) Welche Laufzeitkomplexität hat in Gegenwart von negativen Kantengewichten
(i) die Bestimmung eines minimal aufspannenden Baumes?
(ii) die Bestimmung von kürzesten Pfaden?
(jeweils mit Begründung)
(d) Nenne einen Unterschied zwischen dem Algorithmus von Ford und Fulkerson und dem
von Edmonds und Karp.
(e) Sei e eine Kante in einem Netzwerk, f (e) der Fluss auf e und u(e) die Kapazität von e.
←
Wie lauten die Residualkapazitäten von e und e ?
Viel Erfolg!!!