Übungen: Proportionale Funktionen - Definition
Werbung
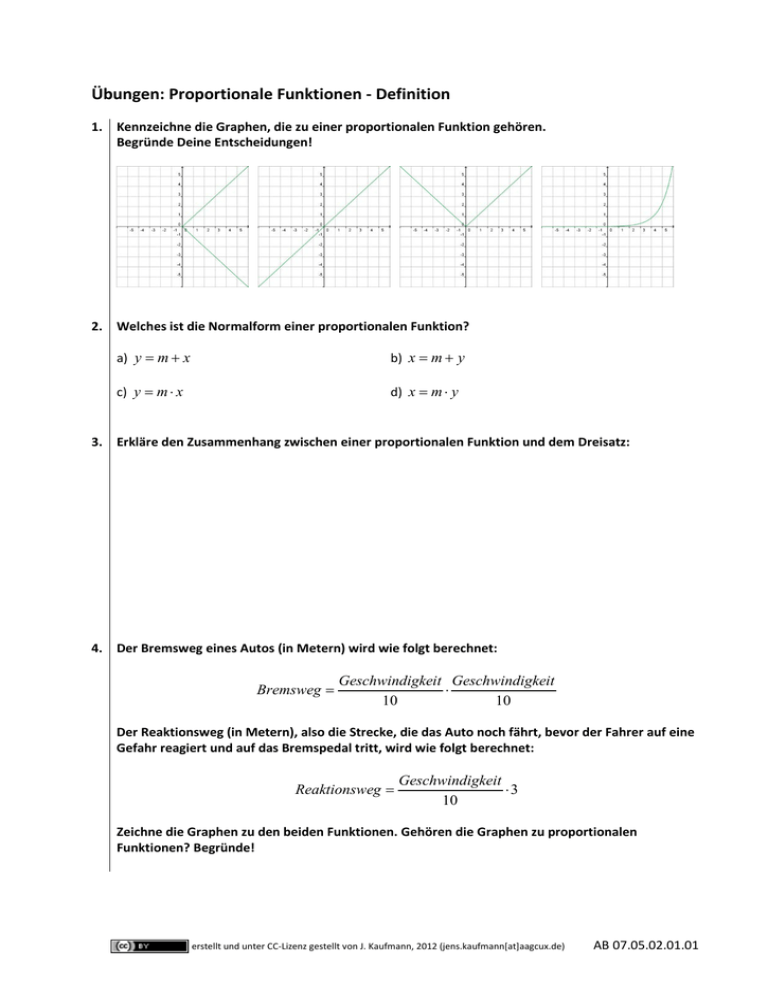
Übungen: Proportionale Funktionen - Definition 1. Kennzeichne die Graphen, die zu einer proportionalen Funktion gehören. Begründe Deine Entscheidungen! 2. Welches ist die Normalform einer proportionalen Funktion? a) y= m + x b) x= m + y c) y= m ⋅ x d) x= m ⋅ y 3. Erkläre den Zusammenhang zwischen einer proportionalen Funktion und dem Dreisatz: 4. Der Bremsweg eines Autos (in Metern) wird wie folgt berechnet: = Bremsweg Geschwindigkeit Geschwindigkeit ⋅ 10 10 Der Reaktionsweg (in Metern), also die Strecke, die das Auto noch fährt, bevor der Fahrer auf eine Gefahr reagiert und auf das Bremspedal tritt, wird wie folgt berechnet: = Reaktionsweg Geschwindigkeit ⋅3 10 Zeichne die Graphen zu den beiden Funktionen. Gehören die Graphen zu proportionalen Funktionen? Begründe! erstellt und unter CC-Lizenz gestellt von J. Kaufmann, 2012 (jens.kaufmann[at]aagcux.de) AB 07.05.02.01.01 Lösungen: Proportionale Funktionen - Definition 1. Kennzeichne die Graphen, die zu einer proportionalen Funktion gehören. Begründe Deine Entscheidungen! Keine proportionale Funktion, da der Graph keine Gerade ist. Ist eine proportionale Keine proportionale Funktion, da der Funktion, da der Graph eine Gerade Graph keine Gerade ist und durch den ist. Ursprung geht. 2. Welches ist die Normalform einer proportionalen Funktion? a) y= m + x b) x= m + y c) y= m ⋅ x d) x= m ⋅ y Keine proportionale Funktion, da der Graph keine Gerade ist. 3. Erkläre den Zusammenhang zwischen einer proportionalen Funktion und dem Dreisatz: Sobald zwei einander zugeordnete Größen proportional zueinander sind, kann der Dreisatz verwendet werden, um fehlende Werte der Größen zu berechnen. Beispiel: Wenn ich weiß, wie viel eine Tafel Schokolade kostet, kann ich mittels Dreisatz auch ausrechnen, wie viel drei, vier oder 543 Tafeln kosten würden. Man kann aber auch ohne Dreisatz mit einer Formel rechnen – und das wäre eine proportionale Funktionsgleichung. Beispiel: Preis insgesamt = Preis einer Tafel Schokolade * Anzahl der gekauften Tafeln 4. Der Bremsweg eines Autos (in Metern) wird wie folgt berechnet: = Bremsweg Geschwindigkeit Geschwindigkeit ⋅ 10 10 Der Reaktionsweg (in Metern), also die Strecke, die das Auto noch fährt, bevor der Fahrer auf eine Gefahr reagiert und auf das Bremspedal tritt, wird wie folgt berechnet: = Reaktionsweg Geschwindigkeit ⋅3 10 Zeichne die Graphen zu den beiden Funktionen. Gehören die Graphen zu proportionalen Funktionen? Begründe! erstellt und unter CC-Lizenz gestellt von J. Kaufmann, 2012 (jens.kaufmann[at]aagcux.de) AB 07.05.02.01.01 Graph zum Reaktionsweg: Reaktionsweg (m) Bremsweg (m) Graph zum Bremsweg: Geschwindigkeit (km/h) Die Größen sind nicht proportional zueinander, da der Funktionsgraph keine Gerade ist. Geschwindigkeit (km/h) Die Größen sind proportional zueinander, da der Funktionsgraph eine Gerade ist und durch den Ursprung verläuft. erstellt und unter CC-Lizenz gestellt von J. Kaufmann, 2012 (jens.kaufmann[at]aagcux.de) AB 07.05.02.01.01