Neutronensterne

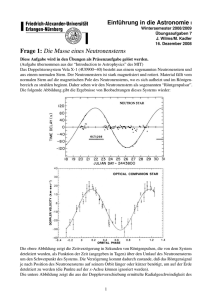
Neutronensterne
von Rishi Horn
[email protected]
Geschichte:
Bereits 1931, also ein Jahr vor der Entdeckung des Neutrons durch Sir James Chadwick, wurden
zwei wichtige Schritte zur Beschreibung eines Neutronensterns getan. Subrahmanyan
Chandrasekhar leitete die nach ihm benannte Massengrenze MCH her. Diese stellt die Obergrenze
der Massen für weiße Zwerge und somit die Untergrenze der Massen für Neutronensterne dar. Noch
im selben Jahr schlug Lew Dawidowitsch Landau theoretisch die Existenz von Neutronensternen
vor. Er bezeichnete diese noch als „Dichte Sterne“. 1933 beschrieben dann erstmals Walter Baade
und Fritz Zwicky die Entstehung eines Neutronensterns. 1939 wurde dessen Masseobergrenze MTOV
von Tolman, Oppenheimer und Volkoff hergeleitet.
Fast 30 Jahre später, also 1967, erfolgte die erstmalige Entdeckung eines Pulsars durch Bell und
Hewish.
Entstehung:
Sterne erzeugen Energie durch Fusion. Durch die Fusion ist eine positive Energiebilanz nur zu
erreichen, solange Elemente mit immer höherer Bindungsenergie pro Nukleon entstehen. Dies ist
nur möglich bis Eisen und Nickel entstehen. Diese Elemente haben die höchste Bindungsenergie
pro Nukleon. Die Fusion stoppt. Dadurch verringert sich der Strahlungsdruck. Der
Gravitationsdruck kann nicht mehr mit genügend Gegendruck kompensiert werden und der Stern
kollabiert. Wie sich der Stern in Folge weiterentwickelt, ist abhängig von dessen Kernmasse:
•
•
•
Für M ≤ MCH entsteht ein durch den Elektronen-Entartungsdruck stabilisierter weißer Zwerg
Für MCH ≤ M ≤ MTOV entsteht ein durch den Neutronenentartungsdruck stabilisierter
Neutronenstern
Für MTOV ≤ M kollabiert der Stern zu einem schwarzen Loch
Entartungsdrücke entstehen da es sich bei Neutronen und Elektronen um Fermionen, also um Spin
½-Teilchen handelt. Diese unterliegen dem Pauli-Prinzip, wonach keine Teilchen mit gleichem Spin
das gleiche Energieniveau besetzen dürfen. Hierbei entspricht dem höchsten besetzten
Energieniveau die Fermi-Energie:
2
E=
h²
(3 π ² ρ )
4πm
3
Hierbei ist h das planksche Wirkungsquantum, m die Masse des Teilchens und ρ die Teilchendichte.
Demnach müssen bei dichterer Teilchenbelegung höhere Energieniveaus belegt werden, was im
Entartungsdruck resultiert. Der Entartungsdruck von Elektronen ist bei Neutronensternen zu
schwach, da Elektronen beim Kollaps in die Protonen „gepresst“ werden. Folgende Gleichung zeigt
den entsprechenden Zusammenhang:
p+e→n+ν e
p steht für das Proton, e für das Elektron, n für das Neutron und νe für das emittierte Neutrino. Der
Neutronenentartungsdruck reicht jedoch zur Stabilisierung aus.
Theoretische Beschreibung:
Aufgrund der extremen Bedingungen im Inneren eines Neutronensterns, ist dessen theoretische
Beschreibung sehr schwer bis unmöglich. Dichten, in hauptsächlich aus Neutronen bestehender
Materie, die bis zu dem 10fachen der Atomkerndichte betragen können sind auf der Erde nicht zu
replizieren. Daher gibt es wenige experimentelle Daten, welche die Varietät der aktuellen Theorien
bestätigen oder widerlegen. Die wichtigste Grundlage einer solchen Theorie bildet die
Zustandsgleichung.
Zustandsgleichung:
Ein zur Beschreibung des Neutronensterns gewähltes Modell, wird durch die Zustandsgleichung
formuliert. Mit dieser wird das System durch seine thermodynamischen Größen beschrieben. Mit
diesen ist es möglich die Tolman-Oppenheimer-Volkoff-Gleichung (TOV-Gleichung) zu lösen und
eine Massenobegrenze zu bestimmen. Werden Neutronensterne größerer Massen entdeckt, ist das
entsprechende Modell auszuschließen. Die Massenobergrenze eines Modells legt fest, ab welcher
theoretischen Kernmasse ein Neutronenstern nicht mehr stabil sein kann und zu einem schwarzen
Loch kollabiert.
TOV-Gleichung:
Die TOV-Gleichung basiert auf dem hydrostatischen Druck p und der Gravitationskraft F. Mit einer
einfachen mathematischen Herleitung erhält man dann die TOV-Gleichung:
dp −G ε(r )M (r )
=
dr
r ²c²
Hierbei steht r für den Radius, G für die Gravitationskonstante, ε für die Energiedichte, M für die
Sternmasse und c für die Lichtgeschwindigkeit. Die Gleichung kann dann durch die Multiplikation
mit speziellen und allgemeinen relativistischen Korrekturfaktoren ergänzt werden.
Hyperonisation:
Ab Dichten, welche in etwa der Atomkerndichte entsprechen, wird die Fermi-Energie hoch genug,
womit die Erzeugung von Strange-Quarks energetisch günstig wird. Energetisch günstig, da die
Strangeness einen weiteren Freiheitsgrad bietet. Die geringere Fermi-Energie bedeutet allerdings
auch, dass sich der Fermidruck verringert und somit die Zustandsgleichung weicher wird. Das
bedeutet, dass es sich um Materie handelt, welche dem Gravitationsdruck schlechter standhalten
kann. Die Folge davon ist, dass Zustandsgleichungen, welche die Hyperonisation berücksichtigen,
eine vergleichsweise geringe Massenobergrenze haben. Diese sind derzeit mit beobachteten
Neutronensternen nicht vereinbar. Die Möglichkeit kann aber noch nicht vollständig
ausgeschlossen werden.
Eigenschaften:
Ein theoretischer durchschnittlicher Neutronenstern hat eine Masse von ungefähr 1.4
Sonnenmassen, einen Radius von 10 km und eine Oberflächengravitation von 2 X 1012 ms-2.
Aufbau:
Zur theoretischen Beschreibung wird der Neutronenstern in Atmosphäre, äußere und innere Kruste
sowie äußeren und inneren Kern aufgeteilt. Diese Bereiche sind nicht diskret voneinander getrennt
sonder gehen vielmehr fließend ineinander über. Manche der Übergangsmechanismen sind noch
nicht vollkommen verstanden.
Atmosphäre: Abhängig von der Temperatur kann diese Schicht zwischen ca. 10cm bei 106K und
wenigen Millimetern bei ca. 105K dick sein. Die Atmosphäre befindet sich im Plasmazustand. Sie
setzt sich aus Eisen, Wasserstoff, Helium und Kohlenstoff zusammen. Ihr Dichte beträgt bis zu 5 X
10-9ρ0, wobei ρ0 die Dichte eines Atomkerns ist (ρ0= 2 X 1014gcm-3). Da diese Schicht durch den
Strahlungsdruck des Neutronensterns stabilisiert wird, sind auch Neutronensterne ohne Atmosphäre
möglich.
Äußere Kruste: Diese Schicht ist mehrere hundert Meter dick und kann Dichten von bis zu 0.002ρ0
aufweisen. Sie besteht größtenteils aus schweren Elementen wie Eisen, welche aufgrund der hohen
Dichten in einer Gitterstruktur angeordnet sind. Die Beschreibung erfolgt über ein Elektronengas
Modell. Dabei ist der Grad der Entartung abhängig von der Tiefe in der sich die Teilchen befinden.
Bei größeren Tiefen degeneriert das Elektronengas bis zu einem idealen Fermigas. Diese Schicht
wird durch den Elektronen-Entartungsdruck stabilisiert, der mit steigender Tiefe immer Größer
wird.
Innere Kruste: Diese Schicht hat eine Dicke von etwa 1km und kann Dichten von bis zu 0.5ρ0
aufweisen. Diese Schicht besteht aus Neutronen, neutronenreichen Kernen sowie freien Neutronen.
Das Auftreten freier Neutronen kommt durch das sog. „neutron-dripping“ zustande. Das bedeutet,
dass bei Neutronenreichen Kernen das emittieren einzelner Neutronen energetisch günstiger wird.
Dadurch trägt auch die starke Wechselwirkung zur Stabilisierung dieser Schicht bei. Aufgrund der
hohen Dichten bestehen nur geringe Abstände zwischen den Teilchen, womit die starke
Wechselwirkung repulsiv wirkt.
Äußerer Kern: Diese Schicht hat eine Dicke von mehreren Kilometern und weist Dichten
zwischen 0.5 und 2ρ0 auf. Sie besteht hauptsächlich aus Neutronen mit einigen Prozent suprafluider
Protonen sowie Elektronen und Myonen. Die Materie ist elektrisch neutral und befindet sich im βGleichgewicht.
Innerer Kern: Der innere Kern hat einen Radius von mehreren Kilometern und weist Dichten bis
zu 10ρ0 auf. Diese Materie ist aufgrund der hohen Dichten und der starken Konzentration an
Neutronen weitestgehend unverstanden.
Aktuelle Forschung:
Die Beobachtung von Neutronensternen erweist sich als äußerst schwierig zum einen wegen des
geringen Radius, zum anderen aber auch wegen der geringen Leuchtkraft, die etwa zehn
Größenordnungen kleiner ist als jene des Vorgängersterns. Somit müssen die hohe Gravitation und
das emittierte Spektrum des Neutronensterns angemessen werden.
Messmethoden:
Atmosphärenstrahlung: Die direkte Messung des abgestrahlten Spektrums bildet eine Ausnahme.
Über derartige Messungen können dann Eigenschaften wie Temperatur oder
Atmosphärenzusammensetzung des Neutronensterns ermittelt werden.
Kepller'scher Gesetze: Diese Messmethode kann nur in einem Doppelsternsystem angewandt
werden. Wichtig ist die gute Beobachtbarkeit des Begleitsterns. Damit sind dann über verschiedene
Observablen Massen und Bahnen beider Sterne bestimmbar.
Pulsare: Ein Pulsar ist eine besondere Art von Neutronenstern mit verschiedenen Eigenschaften.
Pulsare rotieren mit mehreren hundert Hz. Diese kommt von der Rotation des Vorgängersterns.
Durch den Kollaps des Sterns verringert sich der Radius stark, was aufgrund des Pirouetteneffektes
zu einer Verstärkung der Rotation führt. Vom Vorgängerstern erhält der Pulsar auch ein Magnetfeld,
welches aufgrund der hohen Frequenz und der hohen Dichte Stärken von bis zu 108T aufweisen
kann. Durch dieses Magnetfeld wird jede vom Neutronenstern ausgehende Strahlung in von den
Polen ausgehende Jets fokussiert. Der Pulsar kann folglich nur wahrgenommen werden, wenn der
Beobachter von diesem Jet überdeckt wird.
Shapiro-Verzögerung: Dies ist eine relativistische Verzögerung von Licht, welches einen Bereich
starker Gravitation durchquert. Diese Methode kann auf Pulsare in Doppelsternsystemen angewandt
werden. Die stark regelmäßige Strahlung des Pulsars, erfährt eine Verzögerung in Abhängigkeit
davon ob der Begleitstern zwischen Beobachter und Neutronenstern steht. Dadurch ist es möglich
die Masse des Begleitsterns und damit indirekt die Masse des Neutronensterns zu bestimmen.
Ausblick:
Messungen werden nicht nur an Neutronensternen direkt vorgenommen sondern auch in Labors um
die Materie im Inneren besser verstehen zu können. Dies geschieht z.B. indem schwere Ionen
kollidiert werden, um die Materiedichte nachvollziehen zu können. Auch eine Größe, welche die
Komprimierung der Materie nicht beachtet, dafür aber die Asymmetrie zwischen Neutronen und
Protonen widerspiegelt, die Neutronenhaut, wird untersucht. Da allerdings das Innere eines
Neutronensterns nicht nachgebildet werden kann, werden Messungen an Neutronensternen nach
wie vor vorgenommen.