Document

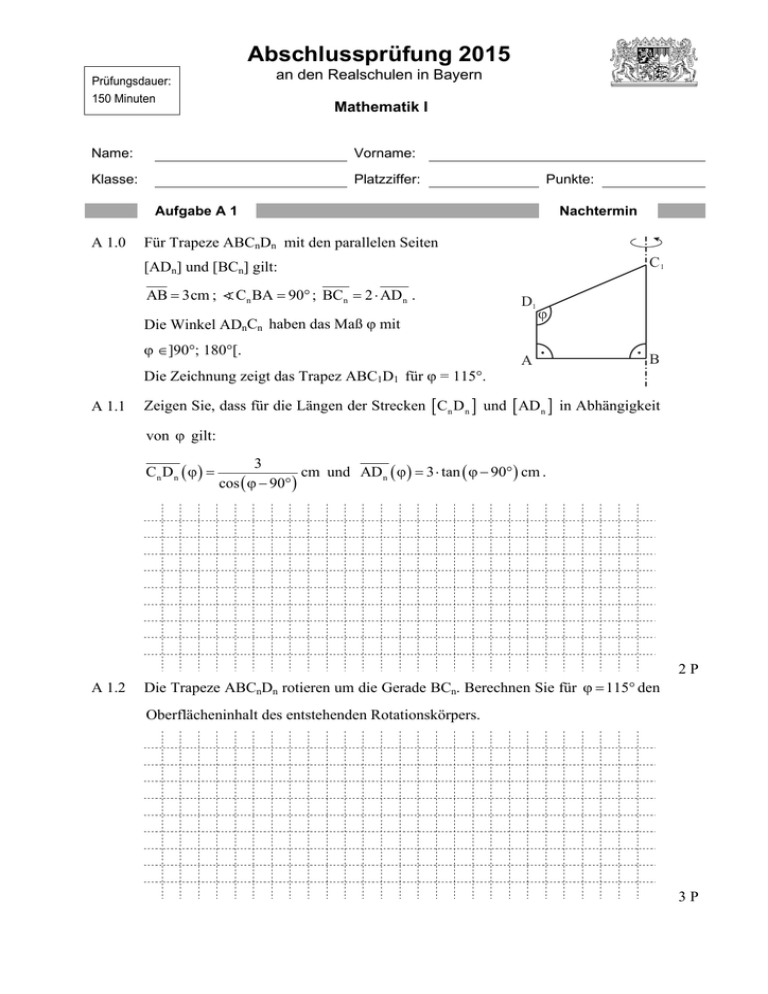
Abschlussprüfung 2015
an den Realschulen in Bayern
Prüfungsdauer:
150 Minuten
Mathematik I
Name:
Vorname:
Klasse:
Platzziffer:
Punkte:
Aufgabe A 1
A 1.0
Nachtermin
Für Trapeze ABCnDn mit den parallelen Seiten
C1
[ADn] und [BCn] gilt:
AB  3cm ;  Cn BA  90 ; BCn  2  AD n .
D1
Die Winkel ADnCn haben das Maß  mit
 ]90°; 180°[.
Die Zeichnung zeigt das Trapez ABC1D1 für  = 115°.
A 1.1
ϕ
A
B
Zeigen Sie, dass für die Längen der Strecken  C n D n  und  AD n  in Abhängigkeit
von  gilt:
Cn Dn    
3
cm und AD n     3  tan      cm .
cos     
2P
A 1.2
Die Trapeze ABCnDn rotieren um die Gerade BCn. Berechnen Sie für    den
Oberflächeninhalt des entstehenden Rotationskörpers.
3P
Aufgabe A 2
Nachtermin
A 2.0 Der Punkt B  3 |1
ist gemeinsamer Eckpunkt von rechtwinkligen Dreiecken
A n BCn , wobei die Punkte A n  x | 0,5x  2  auf der Geraden g mit der Gleichung
 GI  IR  IR  . Die
doppelt so lang wie die Katheten  A n B .
y  0,5x  2 liegen
Hypotenusen
 BCn 
sind dabei stets
A 2.1 Zeichnen Sie die Dreiecke A1BC1 für x  1 und A 2 BC2 für x  4 in das
Koordinatensystem ein.
y
g
1
O
1
x
2P
A 2.2 Begründen Sie, dass für die Winkel Cn BA n gilt: Cn BA n  60 .
1P
A 2.3 Zeigen Sie, dass für die Koordinaten der Punkte Cn in Abhängigkeit von der
Abszisse x der Punkte A n gilt: Cn 1,87x  1,73  1,23x  7,20  .
Aufgabe A 2
Nachtermin
4P
A 2.4 Für das Dreieck A 3BC3 gilt: BC3  g.
Berechnen Sie die x–Koordinate des Punktes A 3 .
2P
Aufgabe A 3
Nachtermin
A 3.1 Die Zeichnung zeigt den Graphen der Funktion f1 mit einer Gleichung der Form
I  IR  IR; a,b  IR  .
y  log 2  x  a   b und die zugehörige Asymptote h  G
Der Graph zu f1 schneidet die y–Achse im Punkt P  0 4  .
Geben Sie die Werte für a und b an.
y
Asymptote h
Graph zu f1
P (0 | 4)
1
O
x
1
2P
A 3.2 Die Funktion f 2 hat eine Gleichung der Form y  a
x 2
 1 , die zugehörige Umkehr-
I  IR  IR; a,b  IR  .
funktion hat eine Gleichung der Form y  log 5 (x  1)  b  G
Bestimmen Sie die Werte für a und b sowie die Wertemenge der Funktion f 2 .
3P
Abschlussprüfung 2015
an den Realschulen in Bayern
Prüfungsdauer:
150 Minuten
Mathematik I
Aufgabe B 1
Nachtermin
I  IR  IR ).
B 1.0 Gegeben ist die Funktion f1 mit der Gleichung y  1,5x 1  2 ( G
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
B 1.1 Berechnen Sie die Nullstelle der Funktion f1 und geben Sie die Gleichung der
Asymptote an.
Zeichnen Sie sodann den Graphen zu f1 für x    6; 4 in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm;  6 < x < 6 ;  3 < y < 6
4P
B 1.2 Der Graph der Funktion f1 wird durch orthogonale Affinität mit der x-Achse als
Affinitätsachse und dem Affinitätsmaßstab k   0,5 sowie anschließende Parallel 3

verschiebung mit dem Vektor v    auf den Graphen der Funktion f 2 abgebildet.
1
Bestätigen Sie durch Rechnung, dass für die Gleichung der Funktion f 2 gilt:
2
I  IR  IR ).
y   1,5x  2 ( G
9
Zeichnen Sie sodann den Graphen der Funktion f 2 für x    6; 6 in das Koordinatensystem zu B 1.1 ein.
4P
B 1.3 Punkte A x 1,5x 1  2 auf dem Graphen zu f und Punkte B  x  2 1,5x  2 
1
n
n 

9




auf dem Graphen zu f 2 haben dieselbe Abszisse x und sind für x < 2,08 zusammen
mit Punkten C n die Eckpunkte von gleichschenkligen Dreiecken A n Bn Cn mit den
Basen  A n Bn  . Für die Höhen  Cn M n  der Dreiecke A n Bn Cn gilt: Cn M n  3 LE .
Zeichnen Sie das Dreieck A1B1C1 für x   2,5 und das Dreieck A 2 B2C2 für x  1
in das Koordinatensystem zu B 1.1 ein.
2P
B 1.4 Zeigen Sie rechnerisch, dass für die Länge der Strecken  A n Bn  in Abhängigkeit von
der Abszisse x der Punkte A n gilt: A n Bn  x    1,72 1,5x  4  LE .
2P
B 1.5 Unter den Dreiecken A n Bn Cn gibt es das gleichseitige Dreieck A 3B3C3 .
Bestimmen Sie durch Rechnung die x–Koordinate des Punktes A 3 .
3P
B 1.6 Begründen Sie, dass es unter den Dreiecken A n Bn Cn kein gleichschenkligrechtwinkliges Dreieck gibt.
2P
Bitte wenden!
Abschlussprüfung 2015
an den Realschulen in Bayern
Prüfungsdauer:
150 Minuten
Mathematik I
Aufgabe B 2
Nachtermin
B 2.0 Das gleichschenklige Dreieck ABC ist die
Grundfläche der Pyramide ABCS.
Der Punkt M ist der Mittelpunkt der Basis
[BC]. Die Pyramidenspitze S ist Eckpunkt des
Dreiecks AMS, das senkrecht auf der Grundfläche ABC steht.
S
Es gilt: AM  6 cm ; BC  9 cm ;
AS  8 cm ;  MAS  120 .
C
M
A
Runden Sie im Folgenden auf zwei Stellen
nach dem Komma.
B 2.1 Zeichnen Sie ein Schrägbild der Pyramide ABCS, wobei
B
 AM 
auf der
Schrägbildachse und der Punkt A links vom Punkt M liegen soll.
1
Für die Zeichnung gilt: q  ;   45 .
2
Zeichnen Sie die Höhe [SF] der Pyramide ABCS ein und berechnen Sie sodann
deren Volumen.
B 2.2 Punkte Pn auf  AS bilden zusammen mit den Punkten B und C Dreiecke Pn BC .
5P
Die Winkel Pn MA haben das Maß  mit   0; 34, 72 .
Zeichnen Sie das Dreieck P1BC für    in das Schrägbild zu B 2.1 ein.
B 2.3 Zeigen Sie, dass für die Länge der Strecken  MPn  in Abhängigkeit von  gilt:
MPn    
5, 20
cm .
sin 120   
1P
2P
B 2.4 Unter den Dreiecken Pn BC gibt es das gleichseitige Dreieck P2 BC .
Bestimmen Sie rechnerisch das zugehörige Winkelmaß  .
3P
B 2.5 Berechnen Sie das Volumen V der Pyramiden ABCPn mit der Grundfläche ABC
und den Spitzen Pn in Abhängigkeit von  .


46,80  sin 
cm3 
 Ergebnis : V    
sin 120   


3P
B 2.6 Die Pyramide SBCP3 mit der Grundfläche SBC und der Spitze P3 hat dasselbe
Volumen wie die Pyramide ABCP3 .
Berechnen Sie das zugehörige Winkelmaß  .
Bitte wenden!
3P