Sterne und Kosmologie

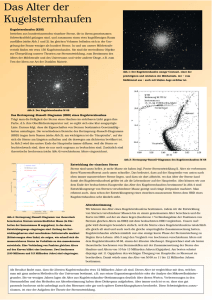
Teil IV
Sterne und Kosmologie
82
Kapitel 11
Vermessung des Universums
Kosmologie ist die Wissenschaft vom Universum als Ganzem. Dabei interessieren
Fragen nach dem Ursprung, dem Alter, dem Inhalt, der Größe und seiner Zukunft.
Das kosmologische Bild ist immer auch von den technischen Entwicklungen geprägt.
Solange man keine Teleskope kannte, nahm man an, der Raum sei gleichmäßig
von den “unveränderlichen” Fixsternen ausgefüllt. Erst mit dem technologischen
Fortschritt entdeckte man immer mehr “Nebel”, deren Natur lange unbekannt war.
Zu Beginn des 20. Jahrhunderts gab es die “Große Debatte” über die Frage, ob
sie andere Welteninseln oder Teil der Milchstraße sind. Entfernungsbestimmungen
waren der Schlüssel zum Verständnis.
Sterne liefern uns nicht nur Informationen aus weit entfernten Bereichen des
Universums, sie erlauben es uns auch, sie zum Vermessen desselben zu verwenden.
Weil wir uns in der Kosmologie mit Raum und Zeit gleichermaßen beschäftigen
müssen (alleine schon wegen der endlichen Lichtgeschwindigkeit), bedeutet das eine
Ausmessung sowohl in räumlicher wie auch zeitlicher Richtung. Wir werden uns
daher jetzt mit Alters- und Entfernungsbestimmungen beschäftigen.
11.1
Altersbestimmungen
11.1.1
Einzelsterne
Wenn wir einen Stern im HRD lokalisiert haben, kennen wir noch nicht sein Alter.
Sind anfängliche Zusammensetzung und Masse bekannt, ist der Entwicklungsweg
im HRD eindeutig vorgegeben, und die Position in rein zeitabhängig. Sie würde
uns daher im Prinzip das Alter liefern. Die Entwicklungswege überschneiden sich
zwar teilweise und es sind auch im Prinzip Mehrfachlösungen möglich, aber diese
Komplikationen lassen sich umgehen. Allerdings sind die Lösungen immer abhängig
von der Vollständigkeit und Genauigkeit der physikalischen Effekte und Annahmen,
die wir in den Modellen verwenden.
Es gibt aber zahlreiche praktische Komplikationen.
1. Masse: sie muss sehr genau bekannt sein, weil stellare Entwicklungsgeschwindigkeiten stark von ihr abhängen. Für massearme Sterne auf der Hauptreihe
zum Beispiel entspricht eine Unsicherheit von nur 0.1 M⊙ bereits einer Altersunsicherheit von 30-40%! Um eine 3%-ige Altersgenauigkeit zu erhalten,
müsste die Masse auf 1% genau bekannt sein. Direkte Massenbestimmungen
gibt es aber nur für Doppelsternsysteme.
2. Zusammensetzung: wie das Beispiel der solaren Zusammensetzung zeigt, sind
die Ergebnisse spektraler Analysen nicht eindeutig, und schließen sich sogar
83
Abbildung 11.1: Das Doppelsternsystem HR6902: die Positionen im HRD sind mit
ihren Fehlern markiert. Die beiden Entwicklungstracks wurden mit Massenwerten gerechnet, die im Einklang mit den aus dem System bestimmten Werten von
3.86 ± 0.15 M⊙ und 2.95 ± 0.09 M⊙ sind. Die chemische Zusammensetzung ist plausibel, aber nicht exakt bestimmt. Das Alter der beiden Komponenten innerhalb der
Fehlerkreuze ist angegeben (Schroeder et al., 1997)
gegenseitig aus. Ein Faktor 2 in Z bei metallarmen Sternen (Pop. II) ergibt
ebenfalls eine Altersunsicherheit von 10%.
3. Entfernung: um die absolute Helligkeit zu bestimmen, braucht man eine genaue Entfernung. Auch diese ist nur bei bedeckenden Doppelstern-Systemen
oder bei nahen Sternen aus Parallaxen bekannt.
4. Farbtransformationen: um vom beobachteten Farb-Helligkeits-Diagramm zum
theoretischen HRD zu kommen, müssen Leuchtkraft und Effektivtemperatur
bestimmt werden. Die dazu notwendigen Transformationen (bolometrischen
Korrekturen) sind unsicher. Umgekehrt ist Teff in den theoretischen Modellen
wegen der Problematik der Konvektionstheorie nicht genau vorhersagbar.
Abbildung 11.1 zeigt das erfolgreiche Modellieren eines gut bestimmten Doppelsternsystems (HR6902). Beide Objekte liegen auf dem Entwicklungsweg für ihre mit
einer Genauigkeit von 5% bestimmten Masse und haben dasselbe Alter. Allerdings
wurde hier das Overshooting als freier Parameter (δov ) behandelt.
Zusammenfassend kann gesagt werden, dass in der Praxis nützliche Altersbestimmungen an Einzelsternen nur in Ausnahmefällen möglich sind, und dass sie
ansonsten eher zum Abschätzen des Alters taugen. In der Zukunft hofft man, dass
die Asteroseismologie neue Wege öffnet, da man dort im Prinzip messen kann, inwieweit der zentrale Wasserstoffgehalt eines Hauptreihensterns schon gesunken ist.
Da dies die “nuklear Uhr” im Stern ist, könnte man damit sein Alter bestimmen.
Auch die Masse könnte aus Oberflächenschwingungen bestimmt werden.
84
Abbildung 11.2: Bild des Kugelsternhaufens M30.
11.1.2
Sternhaufen
Offene und vor allem Kugelsternhaufen (Abb. 11.2) haben die Eigenschaft, dass alle ihre Mitglieder dieselbe Zusammensetzung und dasselbe Alter haben.1 Ein CMD
oder HRD wie in Abb. 7.2 stellt somit eine Momentaufnahme der Entwicklungszustände von Sternen unterschiedlicher Masse dar. Theoretisch wird dies als Isochrone bezeichnet. Die Isochrone zum Alter 0 wäre nur einfach die ZAMS. Sterne
höherer Masse haben bereits die Hauptreihe verlassen, diejenigen mit niedrigerer
Masse haben erst einen Teil ihres zentralen Wasserstoffs verbraucht. Die massereichsten Sterne haben bereits ihr Endstadium erreicht (Weißer Zwerg oder Neutronenstern) und sind aus dem Diagramm weitgehend verschwunden. Da alle Sterne
nach der Hauptreihe zu Roten Riesen werden, ist der Punkt auf der Hauptreihe,
an dem die Sterne sie gerade verlassen, auch der heißeste, und wird Turn-Off der
Isochrone genannt.
Der Vorteil eines KSH-Diagramms ist es, dass wir die Massen der Sterne nicht
kennen müssen. In der einfachsten Behandlung muss – außer der Zusammensetzung
und der Farbtransformation – nur die Entfernung bekannt sein, allerdings bei kosmologischen Altern besser als 0m
. 1 Magnituden (im Entfernungsmodul), weil dies
bereits wieder einer Altersunsicherheit von fast 1 Milliarde Jahren entspricht. Klassisch erhält man die Entfernung aus der Pulsationsperioden–Helligkeits–Beziehung
von RR Lyr Sternen (die aber nicht in allen KSH gefunden werden), neuerdings
auch bevorzugt aus der Helligkeit des Horizontalastes. Es gibt keine direkten Entfernungsmessungen für Kugelsternhaufen mittels Hipparcos-Parallaxen. Statt dessen
bestimmt man eine empirische Hauptreihe aus Einzelsternen mit guten Parallaxen
und ähnlicher Zusammensetzung wie der des Haufens. Der Helligkeitsunterschied
zwischen dieser und der Hauptreihe des Haufens liefert dann die Entfernung. Diese
Methode ist im Prinzip sehr gut, allerdings gibt es jeweils nur sehr wenige Objekte mit passender Metallizität, so dass andere hinzugefügt werden müssen, die
mittels theoretischer Beziehungen auf die gewünschten Häufigkeitswerte transformiert werden müssen. Das ist eine weitere Unsicherheitsquelle neben einer genauen
1 Das gilt natürlich auch nur innerhalb gewisser Genauigkeitsanforderungen. Für fast alle Kugelsternhaufen wurde inzwischen die Existenz mehrerer unterschiedlicher Populationen mit variierenden Häufigkeiten leichterer Elemente (He, O, Na, Mg, Al) nachgewiesen, deren Ursprung aber
noch nicht klar ist. Es scheint sich jedenfalls um eine innere chemische Entwicklung zu handeln.
85
3
2
1
0
-1
3.9
3.8
3.7
3.6
Abbildung 11.3: Zur Konstruktion von Isochronen aus einzelnen Entwicklunswegen
und Isochronen für eine Metalliziät von Z = 0.001 und Alter von 4 bis 8 Mrd. Jahre
(Quelle: BASTI-Datenbank; Cassisi, Pietrinferni, Salaris).
Bestimmung der Rötung des Haufens, welche die Hauptreihe künstlich verschiebt.
Nach Bestimmung der Entfernung und Berechnung theoretischer Isochronen
(Abb. 11.3) – erhalten aus vielen Einzel-Entwicklungswegen von Sternmodellen der
entsprechenden Zusammensetzung und unterschiedlicher Masse – vergleicht man
einfach die Helligkeit des Turn-Offs der Isochronen mit der beobachteten und erhält
so das Alter der Isochrone. Diese sollte dann auch das CMD insgesamt gut reproduzieren, was aber nicht immer der Fall ist wegen der mangelhaften Farbtransformationen. Das sieht man auch in Abb. 11.4, wo aus der Isochrone ein Alter von
ca. 12 Mrd. Jahren bestimmt wurde (typische Ungenauigkeit dieser Methode ist
±1 − 2 Mrd. Jahre). Der Riesenast ist etwas wärmer als die Modelle. Außerdem
sieht man, dass alle Äste des CMD außer der Turn-Off Region wenig bis gar nicht
altersabhängig sind.
Von dieser Methode gibt es Abwandlungen: man kann z.B. statt der altersabhängigen absoluten TO-Helligkeit den Unterschied zwischen TO- und HB-Helligkeit verwenden, da letztere kaum vom Alter abhängt. Das erspart die Bestimmung einer
Entfernung! Oder man verwendet die Farbe des TO, wenn keine Entfernung bekannt
ist, was allerdings wegen der Unsicherheiten der theoretischen Modelle (Konvektionstheorie!) und der Farbtransformationen höchst unsicher ist. Oder man verwendet
eine Kombination aus verschiedenen Altersindikatoren, oder versucht die am besten
passende Isochrone unter Variation von Alter, Entfernung, Rötung und Zusammensetzung zu bestimmen.
Aus Isochronenbestimmungen galaktischer Kugelsternhaufen konnten die Alter
derselben sehr genau bestimmt werden. Mittlerweile stimmen auch unterschiedliche
Autoren in den Ergebnissen weitgehend überein. Danach sind die KSH unserer
Milchstraße maximal 1-2 Milliarden Jahre nach dem Urknall entstanden. (Vor 1996
schien es, als ob die die KSH deutlich älter als das Universum sein könnten.)
11.1.3
Weiße Zwerge
Weiße Zwerge haben die Eigenschaft, dass sie entlang wohldefinierter Kühlkurven
im HRD schwächer und kühler werden. Allerdings verlangsamt sich die Geschwindigkeit zusehend, so dass auch große Altersunterschiede nur noch kleine Änderungen
86
Abbildung 11.4: Beispiel für einen Kugelsternhaufen (IC 4499; [Fe/H]=-1.54; E(B −
V ) = 0.221) und darüber gelegte Isochronen von D. Vandenberg mit Altern von 8
bis 18 Mrd. Jahren (in Schritten von 2 Mrd. Jahren).
hervorrufen, sobald die Sterne etliche Milliarden Jahre alt sind. Dennoch kann man
das Alter einer Population von Weißen Zwergen dadurch bestimmen, dass man den
kühlsten Punkt der Entwicklungswege sucht, an dem überhaupt noch Weiße Zwerge
zu finden sind. Noch leuchtschwächere Punkte wurden einfach aus Mangel an Zeit
nicht erreicht. Abbildung 11.6 zeigt beispielhafte Kühlkurven.
Komplikationen sind
1. die Objekte sind sehr lichtschwach, deswegen kann das Ende der Kühlkurve
auch mangels Entdeckung vorliegen;
2. die Kühlgeschwindigkeit hängt von den genauen physikalischen Effekten im
Stern ab, z.B. Freisetzen latenter Wärme bei der Kristallisation der einzelnen
Elemente;
3. die Kühlkurven hängen von der Zusammensetzung der Weißen Zwerge ab
(Masse der H/He-Hülle);
4. daher sind Weiße Zwerge in Kugelsternhaufen wieder besser geeignet, diese
sind aber viel weiter entfernt als die Weißen Zwerge in der Sonnenumgebung.
Abbildung 11.7 zeigt die Verteilung von Weißen Zwergen in der galaktischen
Scheibe als Funktion der Helligkeit. Durch Vergleich mit theoretischen Erwartungen
wird hier ein Alter dieser Sterne und damit der Scheibe von 9.5 Milliarden Jahren
festgelegt. Auch andere Untersuchungen derselben Art resultieren in Altern von
8-11 Mrd. Jahren.
In Abb. 11.8 ist ein sehr neues Ergebnis dargestellt: die zunehmende Entdeckung
von Weißen Zwergen in Kugelsternhaufen, meist mit dem Hubble Space Teleskop.
Hier ist die Vollständigkeit der Daten noch wichtiger als für Feldsterne, weil die Alter
höher liegen, und die Objekte weiter weg sind. Im gezeigten Fall von NGC6791 liegt
das WD-Alter zwischen 10 und 12 Mrd. Jahren, was auch gut mit dem TO-Alter
übereinstimmt.
87
Abbildung 11.5: Alter von 55 Kugelsternhaufen als Funktion der Metallgehalts
(oben), hier ausgedrückt als [Fe/H] := log (Fe/H)⋆ − log (Fe/H)⊙ , bzw. als Funktion
des galaktozentrischen Radius (unten). Die Ergebnisse wurden aus der IsochronenMethode erhalten (aus Salaris & Weiss 2001)
.
Abbildung 11.6: Kühlalter als Funktion der Leuchtkraft für Modelle kühlender Weißer Zwerge. Oben ist eine detaillierte Rechnung gegen ein einfacheres Kühlmodell
(“Mestel law”) gezeigt, unten der Einfluss der WD-Masse.
88
Abbildung 11.7: Leuchtkraftfunktion (Zahl der Objekte pro Helligkeitsintervall; aufgeführt über den jeweiligen Messpunkten) für Weiße Zwerge in der näheren galaktischen Scheibe. Die Zahl nimmt erwartungsgemäß mit abnehmender Helligkeit zu
(Verlangsamung der Kühlung) und bricht ab, wenn das maximale Alter erreicht ist.
Im Vergleich theoretische Kurven mit Alter von 7 bis 15 Mrd. Jahren.
Abbildung 11.8: Weiße Zwerge im Kugelsternhaufen NGC6791 und Kühlungskurven für Alter von 2, 4, . . . 10 Mrd. Jahren. Dieselben Isochronen sind auch für die
Hauptreihensterne eingezeichnet.
89
11.2
Entfernungsmessungen
Die direkte Methode zur Entfernungsbestimmung ist die Parallaxen-Messung, also
die scheinbare Bewegung eines Objektes am Himmels aufgrund der Bewegung der
Erde um die Sonne. Sie ist sehr genau, kann aber nur in der nächsten Umgebung
angewandt werden. Selbst mit dem astrometrischen Satelliten Hipparcos, der das
CMD in Abb. 1.2 lieferte, erreicht man nur Entfernungen von wenigen kpc.2 Der
2014 gestartete Gaia Satellit wird allerdings genaue Entfernungen zu Millionen von
Sternen, auch im Halo der Milchstraße liefern.
Entfernungsbestimmungen in der Astrophysik beruhen auf zwei grundlegenden
Methoden:
Standardkerzen: es werden Objekte verwendet, deren absolute Helligkeit man sehr
genau kennt, und die am besten universell ist. Dies können Einzelsterne genauso wie ganze Sternsysteme oder Gruppen von Objekten sein. Aus der gemessenen
scheinbaren Helligkeit folgt dann die Entfernung. Zur ersten Gruppe gehören Cepheiden, RR Lyrae Sterne, Supernovae Typ Ia, zur zweiten die Spitze des RoteRiesen-Astes oder die Helligkeitsverteilungsfunktion von Planetarischen Nebeln und
Kugelsternhaufen-Systemen.
Entfernungsleitern: darunter ist zu verstehen, dass man ein jeweils weiter reichendes Entfernungs-Objekt an einem näher befindlichen eicht. Der Grund, warum
man nicht nur das eine benutzt, das am weitesten reicht (Supernovae Ia) ist, dass
es in der Nähe sehr selten, bzw. gar nicht vorkommt. Eine übliche Leiter ist
Parallaxe – Cepheiden – Riesenastspitze/Planetarische Nebel – SN Ia
wobei es auch noch andere Stufen geben kann, und außerdem der erste Schritt,
nämlich Parallaxen von Cepheiden leider nicht sehr genau ist. Die Eichung geschieht z.B. so, dass man Cepheiden-Entfernungen zu nahen Galaxien bestimmt,
und dann deren Riesenastspitze misst. Mit der bekannten Cepheiden-Bestimmung
kann man dann die absolute Riesenast-Helligkeit kalibrieren, wenn man annimmt,
dass Cepheiden und Riesen nicht in unterschiedlicher Entfernung stehen, was meist
wegen der geringen räumlichen Ausdehnung einer Galaxie im Verhältnis zu ihrer
Entfernung eine sehr gute Näherung ist.
Die ideale Standardkerze (die es noch nicht gibt) zeichnet sich durch folgende
Eigenschaften aus:
• sie ist hell, und damit auch in großer Entfernung genau zu vermessen;
• sie ist leicht zu identifizieren;
• sie stellt kein einmaliges Ereignis dar (Wiederholungsmessungen!);
• sie ist lokal kalibriert;
• ihre Eigenschaften sind theoretisch verstanden.
Im Folgenden werden zwei wichtige Entfernungsindikatoren näher besprochen.
11.2.1
Cepheiden
Henrietta Leavitt (Abb. 11.9) entdeckte in der Zeit von 1890–1910, dass die Periode von veränderlichen Sternen vom Typ δ Cephei (Cepheiden) linear mit ihrer
absoluten Helligkeit zusammenhängt. Da die Perioden sich im Bereich weniger Tage
bewegt und die Amplitude bis eine Magnitude reicht (Abb. 11.10), sind sie leicht zu
entdecken und zu vermessen. Ihr Entwicklungszustand wurde schon in Kapitel 7.2
besprochen.
2 Zur
Erinnerung: 1 parsec (pc) ist die Entfernung, unter der die Erdbahn einen Winkel von
1 Bogensekunde einschließt; 1 pc = 3.26 Lichtjahre = 3.08 · 1018 cm
90
Abbildung 11.9: die sogenannten Harvard-Women, eine Gruppe von weiblichen
Astronomen; aufgenommen um 1890. Henrietta Leavitt ist die sechste Dame von
links.
Mit ihrer absoluten Helligkeit von Mv ≈ −4 sind sie bis in den Virgo-Haufen zu
finden, der in einer Entfernung von fast 20 Mpc steht. Insbesondere im HST Key
Project Hubble-Constant haben sie eine große Rolle gespielt. Die damit bestimmte
Hubble-Konstante beträgt danach H0 = 72 ± 8 km/(s Mpc).
Moderne Cepheiden-Perioden-Leuchtkraft-Beziehungen sind ähnlich dieser von
Feast und Catchpole (Periode P in Tagen):
Mv = −2.81 log P − (1.43 ± 0.1)
(11.1)
Die Eichung von Nullpunkt und Steigung hat eine lange Geschichte (Abb. 11.11).
Unsicherheiten bestehen in der Frage, ob die Metallizität einen Einfluss auf die
Beziehung hat. Da Cepheiden außerdem den endlich breiten Instabilitätsstreifen
mehrfach kreuzen, gibt es eine “Farb-Abhängigkeit”, die aber bekannt ist. Am genauesten scheinen Cepheiden im Infraroten Standardkerzen zu sein, wie eine sehr
aktuelle Bestimmung in Abb. 11.12 zeigt.
Abbildung 11.10: Beispiel für die sehr regelmäßige Lichtkurve eines Cepheiden
(links) und die Entdeckungs-Abbildung der PL-Relation von H. Leavitt (rechts).
11.2.2
Spitze des Riesenastes
Wie Abbildungen 5.10 und 7.1 schon zeigten, ist die Leuchtkraft der Spitze des Riesenastes (TRGB) für massearme Sterne in hervorragender Näherung eine Konstante.
Höhere Massen erreichen niedrigere Helligkeiten, so dass die Maximalhelligkeit nicht
verändert wird. Gleichung (10.1) zeigt auch, dass die Abhängigkeit von der Metallizität gering ist. Daher bietet sich die TRGB-Helligkeit als Standardkerze an: sie
ist hell, theoretisch gut verstanden, und sehr konstant. Allerdings ist die Entwicklungsgeschwindigkeit in dieser Phase relativ hoch, so dass nur wenige Sterne dort
zu finden sind. Deswegen ist die Spitze in Kugelsternhaufen nur wenig ausgeprägt,
obwohl diese Systeme 105 bis 106 Sterne beherbergen.
In externen Galaxien ist dies aber anders. Dort sind auch am TRGB genügend
Sterne vorhanden, sie befinden sich alle in etwa derselben Entfernung und damit
91
Abbildung 11.11: Zeitliche Entwicklung der Kalibrierungen von Nullpunkt und Steigung der Cepheiden-Perioden-Leuchtkraftbeziehung. Man beachte, dass jeder neuer
Wert, vor allem des Nullpunktes, das Universum größer oder kleiner macht.
Abbildung 11.12: Eine der neuesten Cepheiden-Perioden-Leuchtkraftbeziehungen,
erhalten aus Messungen an einem 8.2m-Teleskop (VLT) der ESO im Infraroten.
92
Abbildung 11.13: Die Riesenastspitze der S0-Galaxie NGC5128 (Cen A), aufgenommen in den V und I Filtern des Hubble Space Teleskopes. Eingzeichnet sind
auch 10 Mrd. Jahre Isochronen mit Zusammensetzung von 2 bis 158% der solaren
Metallizität sowie die 50 und 90% Niveaus der gezählten Sterne.
ist die TRGB relativ leicht zu finden. Um etwaige Abhängigkeiten von der Zusammensetzung zu umgehen, wird wieder bevorzugt im roten bis nahe infraroten
Licht beobachtet. Abbildung 11.13 zeigt ein Beispiel; die Entfernung wurde hier
mit (m − M ) = 27.98 mag bestimmt. Man beachte auch den weiten Bereich der
Metallizität in dieser S0-Galaxie.
Die Entfernungsmethode der TRGB-Helligkeit reicht etwa genauso weit wie die
mit Cepheiden, ist aber besonders geeignet für Systeme, die nicht in Einzelsterne
aufgelöst werden können. Eine gewisse Schwierigkeit besteht darin, dass zwischen
der theoretischen Helligkeit und der empirisch kalibrierten ein Unterschied von etwa
0.1 mag besteht.
Zum Schluss sei noch erwähnt, dass Supernovae vom Typ Ia eine große Rolle
spielen, da man sie bis in kosmologische Entfernungen entdecken kann (z & 1)
und das Volumen in dieser Entfernung so groß ist, dass sie auch zahlreich sind. Sie
dienen als Standardkerzen, weil ihre Maximalhelligkeit im Ausbruch universell zu
sein scheint (-19.2 mag). Es gibt zwar Abweichungen, die kann man aber über eine
Farbkorrektur berücksichtigen. Auch theoretische Modelle bestätigen zunehmend,
dass SN Ia Standardkerzen sind.
93