7 Multivibratoren - antriebstechnik.fh

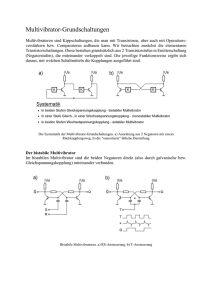
Flip - Flops
7-1
7 Multivibratoren
Multivibratoren sind mitgekoppelte Digitalschaltungen. Ihre Ausgangsspannung springt nur zwischen zwei festen Werten hin und her. Multivibratoren (Kippschaltungen) werden in bistabile, monostabile und
astabile Multivibratoren eingeteilt.
Monostabile Multivibratoren generieren nach einem Triggerimpuls am
Ausgang einen einzelnen Impuls mit einer definierten Impulsdauer. Man
bezeichnet diese Multivibratoren als Mono-Flops.
Bistabile Multivibratoren halten ihren Ausgangszustand (High, Low) so
lange fest, bis sie durch externe Triggersignale zum Umschalten
gezwungen werden. Dieser Zustand bleibt dann bestehen, bis erneut
eine Triggersignalkonfiguration den Multivibrator zum Verändern seines
Zustandes am Ausgang anregt. Typische bistabile Multivibratoren sind
Flip-Flops und Schmitt-Trigger.
Astabile Multivibratoren haben keinen stabilen Zustand am Ausgang. Es
wird kein externes Triggersignal am Eingang des Multivibrators benötigt.
Sie besitzen zwei quasistabile Zustände (High, Low) zwischen denen die
Ausgangsspannung hin und her oszilliert. Man bezeichnet astabile
Multivibratoren auch als Oszillatoren, die mit digitalen Grundschaltungen
realisiert werden.
Die prinzipielle Funktionsweise eines Multivibrators kann mit Hilfe einer
Serienschaltung von zwei Invertern, die über zwei Koppelnetzwerke K1
und K2 miteinander verbunden sind, erklärt werden.
1
K1
u
e1
1
u
a2
K2
Die Steigung der Schaltcharakteristik (siehe Abschnitt 4.4, 4.5 und 6.2)
und damit die Spannungsverstärkung im instabilen Bereich von Invertern
7-2
Multivibratoren
ist >1. Schaltet man zwei Inverter in Serie (ohne Koppelnetzwerke), so
wird die Eingangsspannung ue1 durch beide Inverterstufen verstärkt und
tritt ohne Phasendrehung (Mitkopplung) am Ausgang des zweiten
Inverters auf (ua2 >> ue1). Damit wird eine regenerative Wirkung auf
das Eingangssignal ue1 erreicht.
Die eigentliche Funktion eines Multivibrators wird durch die Art der
Koppelnetzwerke K1, K2 festgelegt. Bestehen beide Netzwerke aus
Serienwiderständen oder Durchverbindungen, dann erhält man einen
bistabilen Multivibrator. Wenn eines der beiden Netzwerke eine
Serienkapazität enthält, werden Gleichspannungen nicht mehr verstärkt.
Nur Spannungsänderungen, deren zeitlicher Verlauf durch die
Ladezeitkonstanten der Serienkondensatoren festgelegt ist, können
verstärkt werden. Diese zeitliche Vorgabe kann als interne Triggerung
interpretiert werden. Monostabile Multivibratoren haben ein kapazitives
Koppelnetzwerk. Astabile besitzen zwei kapazitive Netzwerke.
7.1 Flip - Flops
Die einfachste Form eines bistabilen Multivibrators kann durch die
Serienschaltung von zwei Invertern mit einer Rückkopplung des
Ausganges des zweiten Inverters auf den Eingang des ersten Inverters
(Mitkopplung) erreicht werden (K1, K2 sind Durchverbindungen).
I
1
I
2
1
Q
1
Q
Zur Verdeutlichung der Funktion wird die Rückkopplung des Ausganges
von Inverter 2 auf den Eingang von I1 unterbrochen.
Flip - Flops
7-3
Q
I1
1
I2
Q
1
U
U
I
O
Am Eingang des ersten Inverters wird die Eingangsspannung UI
angelegt. Am Ausgang des zweiten Inverters resultiert dann die
Spannung UO. Um die Schaltcharakteristik nicht verändern zu müssen
wurde angenommen, daß die Eingangswiderstände der Inverter
hochohmig sind. Damit erhält man folgende Schaltcharakteristik der in
Serie geschalteten Inverter:
U0=UI
UO
C
UOH
stabil
instabil
B
UOL
A
stabil
UI
Die eingezeichnete Gerade entspricht UO = UI und entspricht der geschlossenen Rückkopplung (Mitkopplung). Bei einer Spannungsverstärkung >1 und Mitkopplung findet der bistabile Multivibrator bei B
keinen stabilen Arbeitspunkt. Die Richtung der kleinsten Spannungsänderung bei B legt fest, ob der Multivibrator in A oder C seinen stabilen
Zustand findet.
7-4
Multivibratoren
UO
C
UOH
B
UOL
A
UI
In A und C ist die Spannungsverstärkung der Schaltung sehr gering
(Sättigung). Daher behält der bistabile Multivibrator, wenn er einen
Zustand einmal erreicht hat (A oder C), diesen bei, d. h. er speichert
diesen Zustand. Für einen praktischen Betrieb benötigt der bistabile
Multivibrator ein Triggernetzwerk, das die Einstellung eines definierten
Zustandes, der gespeichert werden soll, erlaubt.
7.1.1 Das RS-Flip-Flop
Wenn man an Stelle der Inverter zwei NOR-Gatter mit zwei Eingängen
rückkoppelt, erhält man ein RS-Flip-Flop. Es besitzt die komplementären
Ausgänge Q und Q und die beiden Triggereingänge S (Set) und R
(Reset)
R
1
Q
R
S
S
1
Q
Q
Q
Legt man die folgenden komplementären Eingangszustände fest, so erhält man:
Q ( t n +1 ) = S + Q ( t n )
Q( tn +1 ) = R + Q ( tn )
Flip - Flops
7-5
S = 1, R = 0
Q = S+Q = 1+Q = 0
Q = R+Q = 0+Q = 1
Q wird auf 1 gesetzt (Setzen)
S = 0, R = 1
Q = S+Q = 0+Q = 1
Q = R+Q = 1+Q = 0
Q wird auf 0 gesetzt (Rücksetzen)
Macht man R = S = 0, so bleibt der Ausgangszustand erhalten (Speichern).
Für R = S = 1 werden beide Ausgänge gleichzeitig 0. Der Ausgangszustand ist jedoch nicht mehr definiert, wenn R und S
anschließend gleichzeitig Null werden. Deshalb ist R = S = 1 in der
Regel nicht zulässig (verboten).
Wahrheitstabelle:
R(tn+1)
S(tn+1)
Q(tn)
Q(tn+1)
0
0
0
1
1
0
1
1
0
1
0
1
0
1
0
1
0
1
1
1
0
0
-
Speichern
Setzen
Rücksetzen
Verboten
Übergangsfunktion des RS-Flip-Flop
Q (t n + 1) = R( t n + 1) Q (t n ) + S (t n + 1)
7-6
Multivibratoren
Nachfolgend ist ein RS-Flip-Flop in CMOS Technologie dargestellt.
V
CC
NOR1
NOR2
Q Q
S
S
1
0
0
R
1
Q ( tn +1)
Q( tn +1)
0
VCC
0
VCC
VCC
2
VCC
Q tn
Q tn
0
Qtn
0
Qtn
R
0
1
0
Wie bereits in der Einführung angedeutet, kann ein RS-Flip-Flop auch
mit zwei mitgekoppelten NAND Gattern realisiert werden. Es ist zu
beachten, daß die Triggereingänge jetzt durch die negierten R- und SFunktionen gebildet werden.
S
Q
R
Q
S
R
Q
1
0
1
0
1
1
0
0
Q
1
0
--
C: Clock
S
S
Q
Q( tn +1 ) = S ⋅ C + R ⋅ C ⋅ Q( tn )
C
R
R
Q
Flip - Flops
7-7
7.1.2 Das JK-Flip-Flop
Die Nachteile des undefinierten Zustandes bei R = S = 1 können durch
zwei zusätzliche AND Gatter und entsprechende Rückkopplungen vermieden werden. Der zusätzliche Clock-Eingang (C) ermöglicht die Synchronisation der Ausgangszustände mit dem Clock-Signal.
J
&
S
Q
&
R
Q
Q = J ⋅C ⋅Q + Q
C
Q = K ⋅C ⋅Q + Q
K
J
Q
C
K
Q
J
K
Q
0
0
Q
0
1
0
1
0
1
1
1
Q
Eine Version aus nur NAND-Gattern ist nachfolgend dargestellt.
J
&
&
Q
&
&
Q
C
K
Die Eingänge J und K werden Synchroneingänge genannt. Die ersten
drei Reihen der Wahrheitstabelle stimmen mit dem RS-Flip-Flop überein.
Jedoch, wenn J und K gleichzeitig im High Zustand sind, wird der
Ausgang nach dem Clock-Impuls invertiert. Ist der Clock-Impuls länger
als die Gatter-Verzögerungszeit, dann pendelt (toggle) der Ausgang zwischen Low und High. Da moderne Technologien meist kleine Gatterverzögerungszeiten verglichen mit dem Clock-Impuls aufweisen, ist dies ein
erheblicher Nachteil.
7-8
Multivibratoren
C
t
J
t
K
t
Q
t
toggeln
7.1.3 Das Master-Slave-JK-Flip-Flop
Durch die Kaskadierung von zwei JK-Flip-Flops (Master-Slave) kann
dieser Nachteil vermieden werden.
Master
Slave
PRESET
J
C
&
&
&
&
Q
&
&
&
&
Q
K
1
C
CLEAR
u
C
Clock:
ta tb
tc td
t
t a:
t b:
tc:
t d:
M-S getrennt
M neu aktiv.
J/K getrennt
S übernimmt
Ein positiver Clock-Impuls aktiviert den Master. Er wird in invertierter
Form dem Slave zugeführt. Betrachtet man den Clock-Impulsverlauf, so
Flip - Flops
7-9
erkennt man, daß zum Zeitpunkt ta das Slave- vom Master-Flip-Flop
isoliert wird. Das Slave-FF behält seinen bisherigen Zustand bei. Im
Zeitpunkt tb wird das Master FF-aktiviert. Es verändert in Abhängigkeit
von J, K und Q seinen Zustand. Bei tc wird das Master-NAND-FF von
den Eingängen J,K und Q isoliert. Es behält diesen Ausgangszustand
unabhängig von den Eingängen bei. Im Zeitpunkt td wird die Information
in das Slave -FF übernommen. Es stellt sich der neue Ausgangszustand
Q ein. Der Clock-Impuls muß länger als die Verzögerungszeit des
Master-FF sein. Es existieren keine weiteren Einschränkungen für die
Pulsbreite des Clocks, wenn die J- und K- Pegel in diesem Zeitintervall
konstant sind.
Mit dem PRESET und CLEAR Eingang kann das FF unabhängig vom
Clock-Impuls gesetzt oder rückgesetzt werden. Diese Eingänge dominieren die Clock- oder Synchron-Eingänge.
7.1.4 Das Delay Flip-Flop
Der Zustand des D-Flip-Flop nach dem Clock-Impuls ist gleich dem
Eingangszustand (D) vor dem Clock-Impuls. Es liefert eine Verzögerung,
die sicherstellt, daß der Ausgangszustand sich nicht ändert, bis ein
Clock-Impuls am Flip-Flop anliegt. Man kann das D-Flip-Flop aus einem
RS-FF, einem Inverter und zwei AND Gatter aufbauen.
D
&
S
C
RSFF
1
C
D
Q
&
R
&
&
Q
R
Q0
&
S
&
Q
7-10
Multivibratoren
Das nachfolgende Impulsdiagramm verdeutlicht die Funktionsweise des
D-Flip-Flops.
D
t
C
t
Q
t
set
reset
7.2 Der CMOS Schmitt - Trigger
Der Schmitt-Trigger verwandelt ein verrauschtes oder sich langsam
änderndes Signal in ein digitales Signal. Die prinzipielle Schaltcharakteristik ist nachfolgend dargestellt:
UI
UO
U OH
U OL
U T- U
T+
UI
U
IH
U
IL
U
O
U
OH
U
OL
U
T+
U
Tt
t
Der CMOS Schmitt - Trigger
7-11
Bei der Spannung UT+ schaltet der Schmitt-Trigger von Low auf High.
Bei einer Eingangsspannung von UT- von High auf Low. Ein in CMOS
Technologie realisierter invertierender Schmitt-Trigger besteht aus drei
invertierenden Stufen: einem Schmitt-Trigger-Schaltkreis, Buffer und
Treiber.
Schmitt-Trigger-Schaltkreis
Buffer
V
CC
Treiber
VCC
P1
P2
P3
V
UI
Q
Q
N2
N1
N3
U0
V
CC
UT+=USn+UDSn1
UT-=I UDSp1 I - I USp I
UI = O V: Die beiden p-Kanal-Transistoren P1 und P2 sind leitend. Sie
führen aber einen vernachlässigbar kleinen Drainstrom, weil die beiden
n-Kanal-Transistoren N1 und N2 gesperrt sind. Damit ist Vx = VCC, P3
ist gesperrt und ist N3 leitend. Er wirkt als Source-Folger. Nach den zwei
Inverterstufen ist das Ausgangssignal UO = UOH = VCC. Weil N3
leitend ist sinkt die Drainspannung von N1 auf VCC-USn.
UI = USn: Wenn die Eingangsspannung Usn erreicht, wird N1 leitend
und die Drainspannung von N1 fällt.
UI = UT+: Wenn die Eingangsspannung die obere Triggerschwelle erreicht, wird N2 leitend.
UI = UT+ = UGS2 + UDSN1 = USn + UDSN1
7-12
Multivibratoren
Da N1 und N2 leitend sind, fällt Vx auf 0V, N3 sperrt und P3 wird
leitend. Dadurch nimmt die Drainspannung von P2 ab und sperrt den
Transistor. Der Ausgang des Schmitt-Triggers nimmt den Zustand UO =
UOL = 0V ein.
Beim Übergang von UI = VCC auf UI = 0V treten ähnliche Abläufe im
oberen Teil der Schaltung (Transistoren P1, P2 und P3) auf. Bei UI =
VCC sind die Transistoren P1 und P2 gesperrt. N1 und N2 sind leitend.
Wegen Vx = 0V ist N3 gesperrt und P3 leitend. Die Ausgangsspannung
am Schmitt-Trigger ist 0V. Das Sourcepotential von P1 ist VCC. Wenn
die Eingangsspannung auf VCC - |USp| abfällt, wird P1 leitend. Erreicht
UI die untere Triggerschwelle:
UT- = | USDP1 | - | USp |
so wird P2 leitend. Wenn P1 und P2 leitend sind, steigt Vx auf VCC an
und die Transistoren N3 und P3 werden gesperrt. Die Ausgangsspannung am Schmitt-Trigger ist VCC.
Für einen symmetrischen CMOS Entwurf (Kn1/Kn3 = Kp1/Kp3 = k2 und
USn = |USp| = US) ergibt sich für die Hysteresis des Schmitt-Triggers:
UH = UT+ - UT- = [(1-k) VCC + 2k US] / (1 + k)
Die Hysterese des CMOS-Schmitt-Triggers ist von der Versorgungsspannung abhängig. Das nachfolgende Diagramm verdeutlicht dies.
U
T+
U T-
/V/
U
T+
4
3
U T-
2
1
2
3
4
5
6
VCC / V
Der monostabile Multivibrator (Mono-Flop)
7-13
7.3 Der monostabile Multivibrator (Mono-Flop)
Ein monostabiler Multivibrator (Kippschaltung) besitzt nur einen stabilen
Zustand. Der zweite Zustand ist nur für eine bestimmte Zeit (abhängig
von der Dimensionierung) stabil. Nach Ablauf dieser Zeit kippt die
Schaltung wieder von alleine in den stabilen Zustand zurück. Ein monostabiler Multivibrator kann mit zwei NOR-Gattern aufgebaut werden. Mit
dem Eingang R am ersten Gatter wird der monostabile Multivibrator
getriggert.
R
UR
Q C
1
U
Q
R
VCC
Q
1
Up
U
Q
Für t < to fließt kein Strom durch den Widerstand R. Damit ist up(t < to) =
VCC. Die Ausgangsspannung am zweiten Gatter ist 0V. Damit sind
beide Eingänge des ersten Gatters auf LOW und die
Ausgangsspannung des ersten Gatters beträgt UQ(t<to) = VCC. Die
Spannung über dem Kondensator ist dann 0V. Mit Hilfe eines
Triggerimpulses (UR > US) bei t = t o geht die Spannung von VCC auf
den LOW Pegel über. Während des Spannungssprunges fällt über dem
Kondensator keine Spannung ab. Damit ergibt sich die Spannung am
Ausgang des ersten Gatters im Zeitpunkt t=to zu UQ(t=to) =
[RON/(R+RON)] VCC. Ist der Ausgangswiderstand des ersten Gatters
im LOW Zustand RON sehr viel kleiner als R, so ist die
Ausgangsspannung UQ(t=to) annähernd gleich 0V. Der Kondensator
wird über R geladen und die Spannung up steigt exponentiell an:
up(t>to) = VCC (1 - exp-[(t-to)/([R+RON] C)]
Wenn Up die Schwellenspannung Us erreicht, schaltet das zweite Gatter
auf LOW um. Da der Triggerimpuls nicht mehr anliegt, geht der Ausgang
des ersten Gatters auf HIGH. Die Impulsbreite T ergibt sich zu:
T = [(R+RON) C] ln[VCC/(VCC-US)]
7-14
Multivibratoren
Mit US=VCC/2 und R>>RON ergibt sich: T = 0,69 R C.
Logikpegel für nachfolgendes Impulsdiagramm:
R=1
R=0
Q=1
Q=0
VCC = 5 V
UR =
UR =
UQ =
UQ =
5V
0V
5V
0V
Impulsdiagramm:
U /V/
R
5 t
UQ /V/
5 t
VCC+US
U /V/
p
5 U
S
5V
t
U /V/
Q
5 t
Die Eingangsspannung triggert unabhängig von der Länge des
Triggerimpulses einen Ausgangsimpuls mit einer definierten
Impulsbreite, wenn der Triggerimpuls kleiner als der Ausgangsimpuls ist.
Der astabile Multivibrator
7-15
7.4 Der astabile Multivibrator
Die einfachste Form eines astabilen Multivibrators ergibt sich durch die
Hintereinanderschaltung von einer ungeraden Anzahl von Invertern (n)
und der Rückkopplung des Ausganges des letzten Inverters auf den
Eingang des ersten. Die Frequenz des Ausgangssignales ergibt sich aus
der Verzögerungszeit eines Gatters tpd:
f = 0.5 / (n tpd)
1
1
0
1
1
1
0
1
1
1
0
tpd
Da jedoch die Verzögerungszeit eines CMOS - Gatters von der Temperatur, Versorgungsspannung und kapazitiven Belastung abhängt, ist
diese Anordnung für stabile Oszillatoren nicht geeignet.
Ein einfacher und relativ stabiler Oszillator kann mit zwei NOR - CMOSGattern realisiert werden.
=1
=1
u
O1
u O2
R
C
uX = 0V
7-16
Multivibratoren
Der zeitliche Verlauf der Spannungen am Ausgang des ersten Gatters
uO1, der Spannung am Ausgang des zweiten Gatters uO2 und der
Spannung ux ist nachfolgend dargestellt. Es wurde bei den nachfolgenden Betrachtungen vorausgesetzt, daß die Verzögerungszeiten der
Gatter gleich und die Ausgangswiderstände relativ klein sind.
US: Schaltspannung
u /V/
O1
5 t
t pd
uO2/V/
5-
t
u /V/
x
V +U
CC S
VCC U
S
t
U -V
S CC
t
t2 3
t1
t0
t4
t5
t6
Das zweite NOR-Gatter agiert als Inverter. Damit sind die Spannungen
uO1 und uO2 komplementär zueinander. Angenommen ux(to) befindet
sich unterhalb des Wertes der Schaltspannung US des ersten Gatters.
Der Ausgang des ersten Gatters befindet sich auf HIGH und der des
zweiten auf LOW. ux steigt exponentiell an, da der Kondensator über R
geladen wird. Erreicht ux zum Zeitpunkt t1 den Wert der Schaltspannung
Der astabile Multivibrator
7-17
US, so schaltet nach einer Gatterverzögerungszeit von tpd das erste
Gatter von HIGH auf LOW (Zeitpunkt t2) um. Nach einer weiteren
Gatterverzögerungszeit tpd geht dann das zweite Gatter am Ausgang
von LOW nach HIGH (Zeitpunkt t3). Da der Spannungsabfall über dem
Kondensator gleich der Schaltspannung US ist, nimmt die Spannung ux
nach dem Umschalten des zweiten Gatters den Wert US+VCC an. Die
Spannung ux nimmt exponentiell ab, weil sich der Ausgang des ersten
Gatters auf LOW befindet:
ux(t) =(US + VCC) exp (-t/RC)
T1 ergibt sich aus dieser Gleichung wenn ux(T1) = US gesetzt wird.
Im Zeitpunkt t4 erreicht ux den Wert der Schaltspannung US. Nach der
Gatterverzögerungszeit tpd schaltet das erste Gatter von LOW auf HIGH
um. Nach einer weiteren Gatterverzögerungszeit das zweite Gatter auf
LOW. Da über dem Kondensator im Umschaltzeitpunkt die Spannung
VCC - US abfällt, geht die Spannung ux im Zeitpunkt t6 auf den Wert
US-VCC. Sie würde auf den Wert VCC ansteigen. Deshalb gilt:
ux(t) = VCC - (2VCC - US) exp(-t/RC)
T2 ergibt sich aus dieser Gleichung, wenn ux(T2) = US gesetzt wird. Die
Frequenz des Oszillators berechnet sich zu:
f = 1/(T1+T2)
Mit US = VCC/2 ist T1=T2 und f=1/2.2RC.