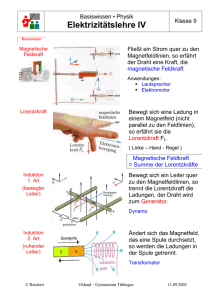
Auf geladene Teilchen, die sich im Magnetfeld bewegen, wirkt die
Werbung

2 Elektrodynamik Der Hall-Effekt M7 Auf geladene Teilchen, die sich im Magnetfeld bewegen, wirkt die Lorentzkraft. Wird ein flächenhafter stromdurchflossener Leiter senkrecht zur Geschwindigkeit der Elektronen von einem Magnetfeld durchsetzt, kann man zwischen den Punkten A und B (Skizze) eine Spannung nachweisen. Benannt ist der Effekt nach dem amerikanischen Physiker Edwin Herbert Hall (1855–1938), der ihn 1879 entdeckte. B UH d – A – – – – – – – – – B b – – – – – + l Aufgabe 1 Erläutern Sie, wie die Richtung der Kraft auf die Elektronen mithilfe der Rechte-Hand-Regel (b S. 86) ermittelt werden kann. Diese Spannung wird als Hall-Spannung bezeichnet. Das Zustandekommen lässt sich mithilfe der Lorentzkraft (b S. 94) deuten: Infolge ihrer Bewegung im Magnetfeld werden die Elektronen im skizzierten Fall nach unten abgelenkt. Es kommt im Punkt B zu einer Vergrößerung und im Punkt A zu einer Verringerung der Elektronenanzahl, demzufolge zu einer Spannung zwischen diesen beiden Punkten. Aufgrund der Ladungsverschiebung bildet sich zwischen den Flächen, an denen sich die Anschlüsse A und B befinden, ein elektrisches Feld der UH Stärke EH = } heraus. Die Verschiebung der Ladungsträger durch die b Lorentzkraft erfolgt so lange, bis Lorentzkraft und Feldkraft im elektrischen Feld gleich groß sind, also gilt: U v ist die Driftgeschwindigkeit der Ladungsträger. Aufgabe 2 Schätzen Sie ab, wie lange ein Elektron braucht, um vom Lichtschalter zur Lampe zu gelangen. Erläutern Sie, warum dennoch die Lampe praktisch sofort nach Betätigung des Schalters leuchtet. H e·v·B = e· } b Damit erhält man für die Hall-Spannung: UH = v · B · b (1) Diese Gleichung kann man nutzen, um die Driftgeschwindigkeit von Elektronen in Metallen abzuschätzen. In einem Experiment wurden für ein dünnes Kupferblech folgende Werte bestimmt: B = 1,25 T; b = 20 mm und UH = 0,024 mV Durch Umstellen der Gleichung (1) nach v erhält man: U H v=} B·b Mit den gegebenen Werten ergibt sich: –5 2,4 · 10 V m = 0,96 mm = 0,96 · 10–3 } v = }} } s s –2 1,25 T · 2 · 10 m Das stimmt gut mit dem in der Literatur häufig genannten Wert von mm 1} überein. s 96 9783835531307_s_082_115_K2_3.indd 96 25.02.2010 22:03:03 Uhr