Bewegung von Ladungsträgern in elektrischen und magnetischen

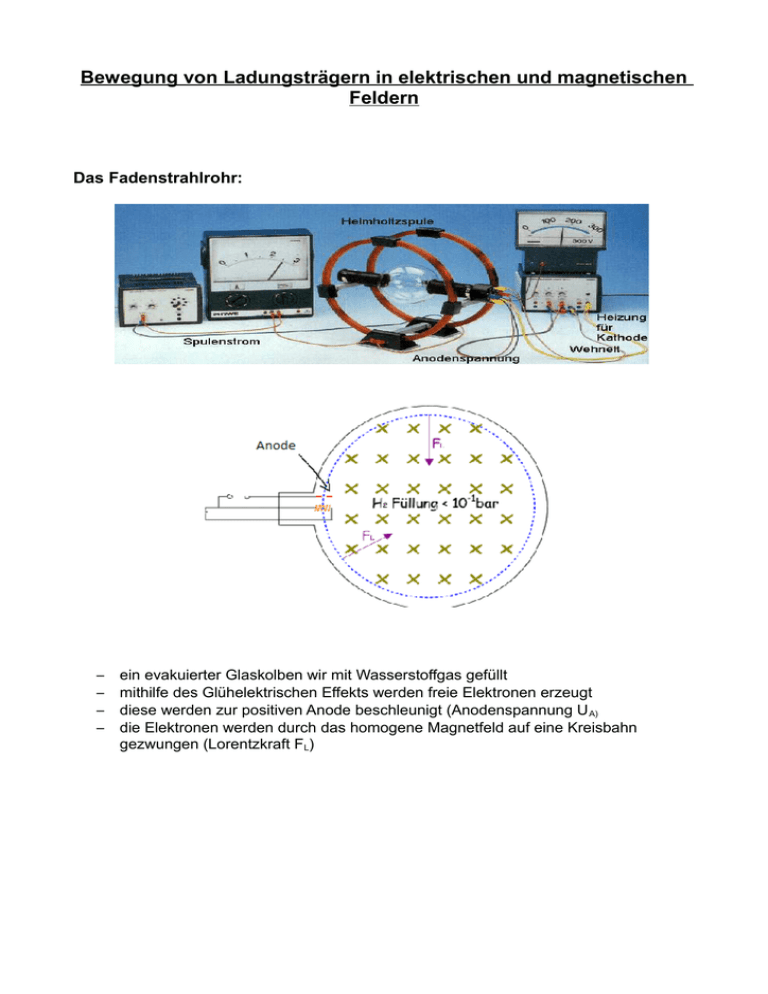
Bewegung von Ladungsträgern in elektrischen und magnetischen
Feldern
Das Fadenstrahlrohr:
–
–
–
–
ein evakuierter Glaskolben wir mit Wasserstoffgas gefüllt
mithilfe des Glühelektrischen Effekts werden freie Elektronen erzeugt
diese werden zur positiven Anode beschleunigt (Anodenspannung U A)
die Elektronen werden durch das homogene Magnetfeld auf eine Kreisbahn
gezwungen (Lorentzkraft FL)
Bestimmung der spezifischen Ladung des Elektrons:
Da die Lorentzkraft hier die Zentripetalkraft für das Elektron aufbringt wird dieser Ansatz
gewählt
Daraus folgt:
(1)
Die Bestimmung der Geschwindigkeit erfolgt über die kinetische Energie
E el = Ekiin
√
V=
(2∗e∗U )
( m)
Durch einsetzen in (1) und quadrieren ergibt sich:
e2
=
m2
2∗e∗U
( B 2∗r 2∗m)
Nun kann man die spezifische Ladung der Elektronen berechnen, da die
Beschleunigungsspannung, wie auch der Radius und die magnetische Feldstärke bekannt
sind.
Da durch die Millikan-Versuch die Elementarladung schon bekannt war, kann man auch
die Elektronenmasse berechnen.
Auch der Radius lässt sich gut in Abhängigkeit der verstellbaren Größen darstellen.
r=
(m∗v)
( e∗B)
Wien-Filter / Wiensches Geschwindigkeitsfilter
–
–
–
–
Elektronen mit der Geschwindigkeit vel werden in den Wien-Filter geleitet
darin wirkt zum einen die Lorentzkraft ( FL ) und die elektrische Kraft (Fel)
entgegengesetzt auf das Elektronen
ist das Elektron zu schnell wird es stärker vom Magnetfeld beeinflusst
ist das Elektron zu langsam wird es stärker vom elektrischen Feld beeinflusst
Damit ein Elektron sich geradlinig durch den Wien-Filter bewegt muss folgendes gelten:
FL = Fel
q∗v∗B=q∗E
E
B
Anwendung des Wien-Filters bei der Massenspektographie:
v=
Herleitung der Elektronenmasse:
m=
(e∗B∗r)
v
Nun sind alle Werte bekannt um die Elektronenmasse zu berechnen.
Hall-Effekt
–
–
–
–
–
Elektronen bewegen sich mit der Geschwindigkeit v durch einen Leiter
dieser wird von einem Magnetfeld durchsetzt
die Lorentzkraft wirkt auf die Elektronen, wodurch sie sich nach oben bewegen
(siehe Abbildung)
dadurch ist eine Spannung UH an den beiden Polen messbar
→ die Hall-Spannung
irgendwann können sich die Elektronen ungehindert fortbewegen, da sich das
Magnetfeld und das elektrische Feld gegenseitig aufheben
Dann gilt:
F el = FL
e∗E =e∗v∗B
U
e∗( H )=e∗v∗B
b
UH = v*b*B
Die Hall Sonde nutzt diesen Effekt um die Magnetfeldstärke zu ermitteln, indem sie die
Hall-Spannung misst und so auf die Magnetfeldstärke schließen kann.
UH
B=
(v∗b)