Allgemeiner Fall - Jagd auf Zahlen und Figuren

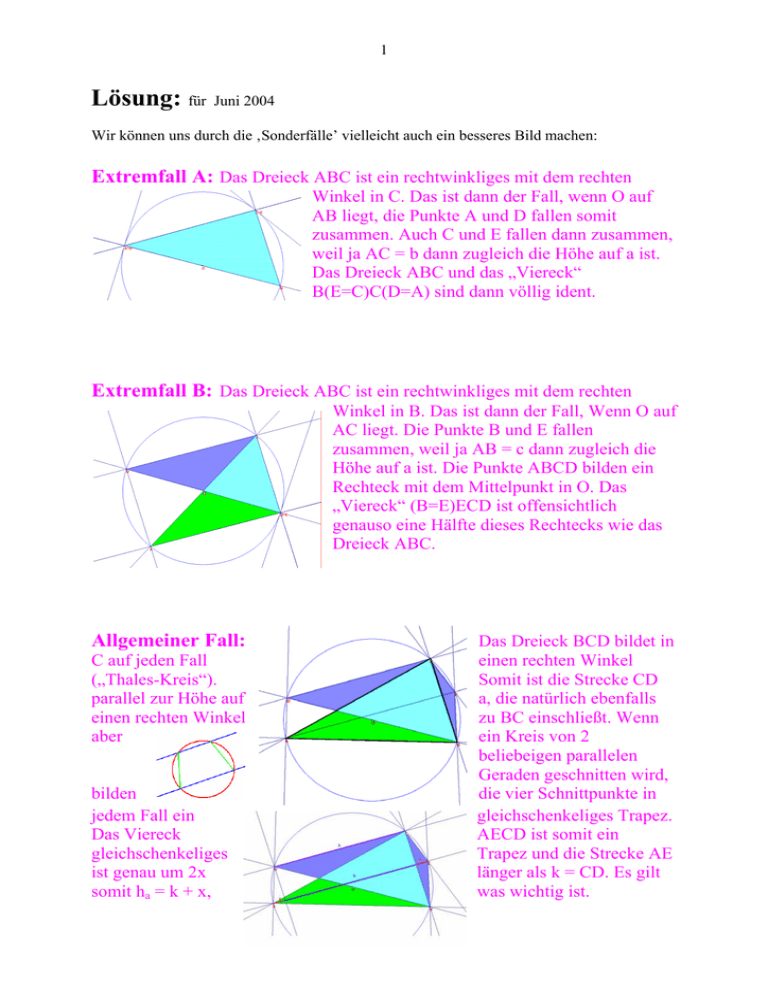
1
Lösung: für
Juni 2004
Wir können uns durch die ‚Sonderfälle’ vielleicht auch ein besseres Bild machen:
Extremfall A: Das Dreieck ABC ist ein rechtwinkliges mit dem rechten
Winkel in C. Das ist dann der Fall, wenn O auf
AB liegt, die Punkte A und D fallen somit
zusammen. Auch C und E fallen dann zusammen,
weil ja AC = b dann zugleich die Höhe auf a ist.
Das Dreieck ABC und das „Viereck“
B(E=C)C(D=A) sind dann völlig ident.
Extremfall B: Das Dreieck ABC ist ein rechtwinkliges mit dem rechten
Winkel in B. Das ist dann der Fall, Wenn O auf
AC liegt. Die Punkte B und E fallen
zusammen, weil ja AB = c dann zugleich die
Höhe auf a ist. Die Punkte ABCD bilden ein
Rechteck mit dem Mittelpunkt in O. Das
„Viereck“ (B=E)ECD ist offensichtlich
genauso eine Hälfte dieses Rechtecks wie das
Dreieck ABC.
Allgemeiner Fall:
C auf jeden Fall
(„Thales-Kreis“).
parallel zur Höhe auf
einen rechten Winkel
aber
bilden
jedem Fall ein
Das Viereck
gleichschenkeliges
ist genau um 2x
somit ha = k + x,
Das Dreieck BCD bildet in
einen rechten Winkel
Somit ist die Strecke CD
a, die natürlich ebenfalls
zu BC einschließt. Wenn
ein Kreis von 2
beliebeigen parallelen
Geraden geschnitten wird,
die vier Schnittpunkte in
gleichschenkeliges Trapez.
AECD ist somit ein
Trapez und die Strecke AE
länger als k = CD. Es gilt
was wichtig ist.
2
Unser Dreieck ABC hat einen Flächeninhalt A1 mit
A1 =
a * ha a * (k + x)
.
=
2
2
Im Rechteck BECD steckt ein rechtwinkliges Dreieck BCD mit der Hypotenuse
BD = 2*R und den Katheten a und k. Sein Flächeninhalt A2 beträgt: A2 =
a*k
.
2
Vom Rechteck BECD ist nach Abzug des Dreiecks BCD nun noch ein Dreieck
BEC übriggeblieben. Dieses hat den Flächeninhalt A3 mit: A3 =
a*x
.
2
Nun ist offensichtlich, dass der Flächeninhalt des Rechtecks BECD =
A2 + A3 =
a * k a * x a * (k + x)
+
=
= A1 gleich ist dem des Dreiecks ABC.
2
2
2
Dieser Lösungsvorschlag stammt von Hr. Wolfgang Gutenbrunner !