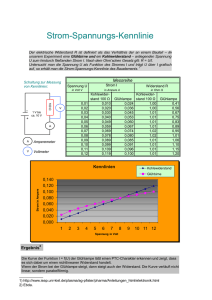
PW1_Messen_Messfehle..

PW1 – Messen und Messfehler
Andreas Allacher 0501793
Tobias Krieger 0447809
Betreuer: Dr. Wilhelm Markowitsch
17. und 25.Okt 2006
Anfängerpraktikum 1 - PW1
Allacher & Krieger
1. GRUNDLAGEN ...................................................................................................................................... 3
1.1 MESSEN UND FEHLER ............................................................................................................................ 3
1.2 FEHLERARTEN ........................................................................................................................................ 4
1.2.1 STATISTISCHE FEHLER ..................................................................................................................... 4
1.2.2 SYSTEMATISCHE FEHLER ................................................................................................................. 4
1.3 FEHLERAUSWERTUNG - ÜBERBLICK................................................................................................... 5
2 AUSWERTUNG ....................................................................................................................................... 7
2.1 MESSAUFGABE TEIL 1 – MECHANIK ................................................................................................... 7
2.1.1 QUERSCHNITTSBESTIMMUNG .............................................................................................................. 7
2.1.2 WINKELNONIUS .................................................................................................................................. 12
2.1.3 DICHTEBESTIMMUNG ......................................................................................................................... 13
2.1.4 ERDBESCHLEUNIGUNG ....................................................................................................................... 16
2.2 MESSAUFGABEN TEIL 2 – ELEKTRISCHE MESSUNGEN .................................................................. 20
2.2.1 GENAUIGKEIT ELEKTRISCHER MESSUNGEN ..................................................................................... 20
2.2.2 MESSUNGEN MIT GLEICHSPANNUNG ................................................................................................ 20
2.2.3 SPANNUNGSTEILER BEI WECHSELSTROM ......................................................................................... 32
2.3 MESSAUFGABEN TEIL 3....................................................................................................................... 36
2.3.1 U0 UND RI EINER REALEN STROMQUELLE ......................................................................................... 36
2.3.2 BELASTETER SPANNUNGSTEILER ...................................................................................................... 39
4. FORMELN ............................................................................................................................................. 44
Seite 2
Anfängerpraktikum 1 - PW1
Allacher & Krieger
1. Grundlagen
1.1 Messen und Fehler
Eine Hauptaufgabe der Physik ist es, über experimentelle Versuche Vorgänge unserer
Umwelt nachzustellen, zu beobachten, die Informationen zu erfassen und aus den Daten die
richtigen Schlüsse zu ziehen. Dieses Nachstellen dient unter anderem zum Untermauern (oder
zum Widerlegen) von bestehenden Theorien aber auch für die Folgerung für neue Theorien.
Die Untersuchung eines Phänomens erfolgt oft leichter durch Zerlegung eines großen
Prozesses in einige, möglichst unabhängige kleine, die wir in einer kontrollierbaren
Umgebung schließlich besser beurteilen können. Diese kontrollierbare Umgebung nennen wir
meist Laborbedingung. In diesem Raum sind die meisten äußeren Faktoren wie z.B.
Temperatur, Luftbewegung,...bekannt und dadurch ist der Einfluss auf den Versuch
abschätzbar.
Die Nachstellung eines Vorganges sollte möglichst getreu dem Original erfolgen um die
Auswirkungen in Relation zum Auslösenden Moment zu kennen. Ist der Einfluss und die
dadurch ausgelöste Wirkung bekannt, können wir Zusammenhänge bilden und erfassen.
Um die richtigen Schlüsse zu ziehen, brauchen wir die richtigen Informationen. Wir sollten
wissen, was wir erreichen wollen und darauf vorbereitet sein. Die resultierenden
Informationen müssen erfasst und geordnet werden. In einigen Fällen (z.B. als Bestätigung
einer Theorie) entsprechen die Ergebnisse den Erwartungswerten. In anderen Fällen müssen
die Werte erst in Korrelation zueinander gebracht werden um die richtigen Schlüsse zu
ziehen.
In diesem gesamten Ablauf der Informationsgewinnung müssen Fakten nachgestellt, erfasst
und verarbeitet werden. Es werden dadurch Daten gewonnen. Einzelne Daten sind ohne
Aussage. Jedoch viele Daten die in einem konkreten Zusammenhang stehen, können eine
Aussagekraft haben. Der Zusammenhang ist jedoch nur gegeben, wenn die Daten richtig und
möglichst vollständig erfasst werden. In einigen Fällen können auch bereits kleine
Abweichung der Daten, große Auswirkungen im Ergebnis haben.
Irren ist menschlich. Irren ist normal. Wir sollten uns diesem Fakt bewusst sein. Fehler
entstehen und werden gemacht. Kein noch so genaues Experiment ist nicht mit
Abweichungen belastet. Ein Fehler stehlt kein so großes Problem dar, wenn er bekannt ist und
möglichst klein gehalten wird. Der Fehler kann an mehreren Stellen passieren. Bereits in der
Grundidee, beim Versuchsaufbau, beim Ablauf, bei der Erfassung oder bei der Auswertung.
Oder in allen. Entsteht der Fehler bereits am Anfang, so ist das Ende äußerst ungewiss.
In vielen der kleinen Schritte die wir machen müssen um ein Ergebnis zu erzielen, müssen wir
messen. Längen, Zeit, Temperatur, Druck, Spannung, Strom, Kraft, Auslenkungen,.... Viele
Möglichkeiten um Fehler zu machen. Wir sprechen dabei von Messfehler. Messfehler sind
Ungenauigkeiten die entweder auf zufällige Einflüsse zurückgehen – wir sprechen dann auch
von statistischen Fehlern, oder aber deren Ursache in der Ungenauigkeit der Messinstrumente,
des Durchführenden und/oder der Messbedingungen liegen. Dabei sprechen wir von
systematischen Fehlern.
Seite 3
Anfängerpraktikum 1 - PW1
Allacher & Krieger
1.2 Fehlerarten
Die unterschiedlichen Fehlerarten treten meist miteinander aus. Durch eine genaue
Auswertung der Messergebnisse lassen sich Rückschlüsse auf die möglichen Fehlerquellen
ziehen. Um ein möglichst aussagekräftigen Ergebnis zu erhalten, sollte die Messung unter
gleichen Bedingungen mehrmals durchgeführt und dabei ein genaues Messprotokoll erstellt
werden. Mehrer Messungen werden zu Messreihen. Ein konkretes Auswerten der Messreihen
zeigt uns die Richtigkeit und die Präzession der Messung. Jede Messung ist ein Eingriff in das
zu messende System und beeinflusst dieses. Messen wir z.B. die Leerlaufspannung einer
Batterie mithilfe eines Voltmeters, so fließt ein kleiner aber doch vorhandener Strom und wir
messen nur noch eine Klemmspannung. Wer misst, misst Mist. Wir werden nie ein ideales
Messsystem haben!
1.2.1 Statistische Fehler
Ihre Ursache liegt im Dunkeln. Jede Messung die wiederholt wird, hat eine (leichte)
Abweichungen von der vorhergegangen Messung. Es fließen verschieden Störgrößen in die
Messung ein welche wir kaum beeinflussen können. Die Auswirkung eines statischen Fehlers
zeigt sich in Abweichungen in beide Richtungen. Je größer der statische Fehler ist, umso
entfernter werden die Messergebnisse vom Mittelwert aller Messungen liegen. Der statistische
Fehler kann präzise oder unpräzise sein. Je näher die einzelnen (wiederholten) Messungen an
dem Mittelwert liegen, desto präziser ist die Messung.
1.2.2 Systematische Fehler
Landen auf fruchtbaren Boden wenn wir z.B. Messgeräte mit hoher Toleranz verwenden. Das
bedeutet, zeigt das verwendete Messgerät zu ungenau bzw. einfach falsch an, so fließt dieser
Fehler in die Messung ein. Auch der Messdurchführende kann einen Fehler verursachen. Sei
es durch leichte Ablesefehler, z.B. bei ungenauer Zeitmessung oder ungenaues Ablesen eines
Messgerätes. Ebenfalls eine mögliche Ursache liegt darin, wenn sich die Messbedingungen
ändern. Der Systematische Fehler zeigt sich vor allem durch die Abweichung von einem
Sollwert (Erwartungswert) in eine bestimmte Richtung. Auch der Mittelwert einer Messreihe
wird nicht dem Sollwert entsprechen. Weicht der Messwert stark von dem Sollwert ab, so ist
das Messergebnis unrichtig.
Seite 4
Anfängerpraktikum 1 - PW1
Allacher & Krieger
1.3 Fehlerauswertung - Überblick
Die Auswertung von Messreihen ist die Aufgabe der Fehlerrechnung. Anhand der
Messergebnisse wollen wir auf den wahren Wert der gemessen Größe schließen und auch die
Zuverlässigkeit unserer Messung überprüfen.
Wir bilden den arithmetischen Mittelwert einer Messreihe durch das Summieren der einzelnen
Messwerte und dividieren dieses Ergebnis durch die Anzahl der Messungen.
1 N
x = ! xi
N i=1
Der Absolute Fehler ist die Differenz von Erwartungswert und Messwert.
! a = E rwartet " M essung
Der Relative Fehler ist der Quotient aus der Abweichung und Erwartungswert mal 100.
!r =
"m
•100%
x
Die Standardabweichung ist ein Maß für die statistische Abweichung der Messwerte um den
Mittelwert.
!=
1 N
(x i " x ) 2
#
N " 1 i=1
Haben wir in einer Grundgesamtheit von Messergebnissen mehrere gleiche Werte, so können
wir gleiche Werte nach ihrer Häufigkeit zusammenfassen. Wir können diese zu einem
Histogramm zusammenfassen. Meistens liegen die meisten kleinen Abweichungen nahe am
Mittelwert, und stärkere Abweichungen weiter außen.
Seite 5
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Eine Verteilungsfunktion F(x) steht für die Wahrscheinlichkeit einen Messwert zu beobachten
der kleiner oder gleich x ist. Dafür muss die Summe der Wahrscheinlichkeitsfunktionen
normiert sein. Im allgemeinen Fall verteilen sich die Messfehler anhand der Gauß’schen
Normalverteilung.
(x $x 0 )
1
$
2" 2 dx
! (x)dx =
e
" 2#
2
$%
& ! (x)dx = 1
+%
Dabei erwarten wir, dass rund 68% der Messwerte innerhalb des Bereiches der einfachen
Standardabweichung, 95% der Messwerte innerhalb eines Bereiches der doppelten
Standardabweichung und 99,7% der Messwerte innerhalb des Bereiches der dreifachen
Standardabweichung liegen.
Bei einer Messung entstehen die Fehler meist an mehreren Stellen. Wir müssen beachten, dass
ein Fehler in einem Teil der Messung sich in einen anderen Teil ebenfalls auswirkt. Dies
passiert z.B. leicht bei indirekten Messmethoden. Wir sprechen dann von der
Fehlerfortpflanzung.
2
2
2
k
# "f &
# "f &
# "f &
! = % ( ! 12 + .... + % ( ! k2 = ) % ( ! i2
$ "x1 '
$ "x k '
i=1 $ "x i '
2
y
Die Bildung einer Ausgleichsgeraden erfolgt durch Lineare Regression.
y = ax + b
n
# n 2 n
&
N = n% ! x i " ! x i ! x i (
$ i=1
'
i=1
i=1
a=
n
n
,
1) n
(n
x
y
)
"
x
!
!
i i
i ! yi .
+
N * i=1
i=1
i=1
-
b=
n
n
,
1)n 2 n
x
y
"
x
!
!
i ! i
i ! xi yi .
+
N * i=1 i=1
i=1
i=1
-
Alle sonstigen Formeln werden entweder in den einzelnen Abschnitten behandelt oder sind in
Kapitel 4 aufgegliedert.
Seite 6
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2 Auswertung
2.1 Messaufgabe Teil 1 – Mechanik
2.1.1 Querschnittsbestimmung
Bei den ersten Versuchen üben wir den Umgang mit verschiedenen mechanischen
Messinstrumenten. Es soll der Querschnitt eines dünnen Drahtes ermittelt werden. Dabei
achten wir besonders auf möglichen Fehlerquellen und beurteilen unsere Messergebnisse und
den Einfluss von Messfehlern.
Bei allen drei folgenden Messgeräten wird die Genauigkeit der Ablesung über einen so
genannten „Nonius“ unterstützt. Der Nonius steht immer in einem bestimmten
Teilungsverhältnis zur Hauptskala (9/10,19/20,39/40,...). Je nach Teilungsverhältnis befinden
sich dann auf der Noniusskala z.B. bei 19/20, 20 Teilstriche im Abstand von 0,95mm. Durch
das Verhältnis stimmt genau ein Noniusstrich mit genau einem Teilstrich der Hauptskala
überein. Beträgt der Nonius z.B. 39/20, so ist eine Ablesung auf 0.05mm möglich.
Die Ablesegenauigkeit welche durch den Nonius des Messgerätes bestimmt wird, bestimmt
ebenfalls die Abweichung des Messgerätes. Ist die berechnete Standartabweichung kleiner als
die Abweichung des Messgerätes, so nehmen wir die Abweichung des Messgerätes. Ist jedoch
die Standartabweichung größer als die Abweichung des Messgerätes, wird unsere ermittelte
Standartabweichung angegeben.
Verwendete Abkürzungen
Zeichen
Xyz...
<xyz...>
S
Bedeutung
Wert
Mittelwert
Standardabweichung
sm
∆xyz...
H
G
Standardabweichung des Mittelwerts
Abweichung des Wertes uim Mittelwertes
Absolute Häufigkeit
Relative Häufigkeit / Gewichtung
σ2
Varianz
εA
Absoluter Fehler
εR
Relativer Fehler
I
Messung 1,2,3,…
Seite 7
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.1.1.1 Schublehre
Die von uns verwendete Schublehre hat eine Noniusangabe von 39/20. Somit ist eine
theoretische Ablesegenauigkeit von 0,05 mm gegeben. Wir wiederholen unsere Messung
sechs Mal, dabei wechseln wir uns bei jeder Messung ab. Liegt ein Wert bei einer Ablesung
zwischen zwei Skaleneinheiten, haben wir diesen Wert auf die dritte Kommastelle genau
angegeben (+/- 0,005mm).
Messwerte
I
1
2
3
4
5
6
Summen
di [mm]
0,200
0,250
0,300
0,275
0,325
0,300
1,650
Δ di [mm]
-0,075
-0,025
0,025
0,000
0,050
0,025
0,000
Δ d2i [mm]
0,006
0,001
0,001
0,000
0,003
0,001
0,010
s [mm]
0,045
εA[mm]
0,045
εR [%]
16,364
Auswertung der Daten
<d> [mm]
0,275
Ergebnis laut Messauswertung:
d=0,275 ±0,045 mm
Da jedoch die Genauigkeit des Messgerätes bei ±0,05mm liegt, gilt die Abweichung der
Schublehre. Daraus folgt das Ergebnis:
d=0,275 ±0,05 mm
Häufigkeitsverteilung
J
1
2
3
4
5
Summen
di [mm]
0,2
0,25
0,275
0,3
0,325
1,35
hi
1
1
1
2
1
6
gi [mm]
0,167
0,167
0,167
0,333
0,167
1,000
digi [mm]
0,033
0,042
0,046
0,100
0,054
0,275
Δ d[mm]
-0,0750
-0,0250
0,0000
0,0250
0,0500
Δ d2 gi [mm2]
0,0009
0,0001
0,0000
0,0002
0,0004
0,002
Seite 8
Anfängerpraktikum 1 - PW1
Allacher & Krieger
<d> [mm]
s [mm]
sm [mm]
0,275
0,046
0,021
Ergebnis anhand der Gewichtung nach Durchmesserklassen:
d=0,275 ±0,046 mm
Auch hier ist die Abweichung der Schublehre anzunehmen, d.h.
d=0,275 ±0,05 mm.
2.1.1.2 Mikrometerschraube
Die Mikrometerschraube ist bei richtiger Anwendung genauer als eine Schublehre. Bei
richtiger Anwendung sollte eine Ablesegenauigkeit von bis zu 0,01 mm möglich sein. Falls
eine Ablesung zwischen zwei Skaleneinheiten liegt, nehmen wir die goldene Mitte von 0.005
mm für die letzte Stelle an.
Messwerte
I
1
2
3
4
5
6
Summen
di [mm]
0,2300
0,2300
0,2350
0,2290
0,2300
0,2250
1,3790
Δ d2 [mm*10-4]
0,0000
0,0000
0,2500
0,0100
0,0000
0,2500
0,5100
Δ di [mm]
0,00000
0,00000
0,00500
-0,00100
0,00000
-0,00500
-0,00100
Auswertung der Daten:
<d> [mm]
0,2300
S [mm]
0,0030
sm [mm]
0,0010
εA[mm]
0,0030
εR
0,0130
Anhand unserer Werte kommen wir zu folgenden Ergebnis:
d=0,23 ±0,003 mm
Die kleinste mögliche Skalenteilung des Mikrometers ist jedoch 1/100 und somit größer als
die von uns Ermittelte. Wir geben daher die Genauigkeit des Mikrometers an:
d=0,23 ±0,01 mm
Seite 9
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Häufigkeitsverteilung:
J
1
2
3
4
Summen
di [mm]
0,225
0,229
0,23
0,235
0,919
hi
1
1
3
1
6
gi [mm]
0,167
0,167
0,500
0,167
1,000
<d> [mm]
0,23
digi [mm]
0,038
0,038
0,115
0,039
0,230
s [mm]
0,003
Δ d[mm]
-0,0050
-0,0010
0,0000
0,0050
Δ d2 gi [mm2]
0,000004
0,000000
0,000000
0,000004
0,000008
sm [mm]
0,002
Wir erhalten anhand der Gewichtung der Durchmesserklassen das Ergebnis:
d=0,23 ±0,003 mm
Weil unsere Standardabweichung geringer als die kleinste Einteilung des Mikrometers ist,
nehmen wir wieder die Genauigkeit des Mikrometers an:
d=0,23 ±0,01 mm
2.1.1.3 Mikroskop
Das Mikroskop wird als Längenmessgerät verwendet. Im ersten Schritt muss der im Okular
eingeblendete Maßstab durch einen Normalmaßstab kalibriert werden. Unser Normalmaßstab
hat eine Teilung von 200 Strichen auf 2 mm. 40 Teilstriche des Okularmaßstabes bei einer
400fachen Vergrößerung entsprechen 0,1mm, somit ist der Abstand zwischen zwei
Teilstrichen des Okularmaßstabes 0,0025mm.
Das Mikroskop ist zwar wesentlich genauer bei richtiger Bedienung, jedoch auch dadurch
offener für mögliche Fehlerquellen. Ist es falsch eingestellt, z.B. ist dass betrachtete Objekt
unscharf, so verfälscht die Unschärfe aufgrund der enormen Vergrößerung das Messergebnis
beträchtlich.
Messergebnisse
I
1
2
3
4
5
6
Summen
di [mm]
0,2250
0,2325
0,2225
0,2325
0,2300
0,2300
1,3725
Δ di [mm]
-0,0038
0,0038
-0,0063
0,0038
0,0013
0,0013
0,0000
Δ d2i [mm*104]
0,1406
0,1406
0,3906
0,1406
0,0156
0,0156
0,8438
Seite 10
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Auswertung der Daten:
<d> [mm]
0,2288
s [mm]
0,0041
sm [mm]
0,0017
εA[mm]
0,0041
εR [%]
0,0179
Bei diesem Messverfahren ist die Standardabweichung größer als die kleinste Einteilung des
Maßstabes, darum geben wir hier den absoluten Fehler an:
d=0,2288 ±0,0041mm
Häufigkeitsverteilung
j
1
2
3
4
Summen
di [mm]
0,2225
0,225
0,23
0,2325
0,91
hi
1
1
2
2
6
gi [mm]
0,167
0,167
0,333
0,333
1,000
<d> [mm]
0,2288
digi [mm]
0,037
0,038
0,077
0,078
0,229
s [mm]
0,0043
Δ d[mm]
-0,0063
-0,0038
0,0013
0,0038
Δ d2 gi [mm2]
0,000007
0,000002
0,000001
0,000005
0,000014
sm [mm]
0,0022
Unsere Auswertung ergibt somit:
d=0,2288 ±0,0043mm
2.1.1.4 Messgruppen
Da dasselbe Werkstück mit unterschiedlichen Messgeräten vermessen wurde, haben wir nun
die Möglichkeit eine Gewichtung der verschiedenen Messmethoden vorzunehmen.
I
smi
[mm]
smi2 *10-2
[mm2]
1
0,0183
2
0,0012
3
gi
<d>
[mm]
0,0333
30,0000
0,0001
6718,6240
0,0017
0,0003
0,0212
0,0338
gidi
Δ d2
Δd2gi
0,2750
8,2500
0,0020521
0,0616
0,2300
1545,2835
0,0000001
0,0006
3555,5556
0,2288
813,3333
0,0000009
0,0032
10304,1796
0,7338
2366,8669
0,0020531
0,0654
<d>g [mm]
0,2297
sgm [mm]
0,001454262
Das gewogene Mittel beträgt rund d=0,23mm mit einer Genauigkeit von ±0,0015 mm.
Seite 11
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.1.2 Winkelnonius
Die Winkeln eines schiefwinkligen Dreiecks sind mithilfe einer Winkellehre zu vermessen.
Der angegebene Winkelnonius beträgt 5´ (in Grad 0,0833°). Die Summe aller Winkel beträgt
180°.
Bei dieser Übung ergibt sich der Gesamtwinkel aus der Summer der gemessen Einzelwinkel.
Deshalb fließen die Fehler jeder Messung ebenfalls in die Gesamtrechnung ein. Es kommt zu
einer Fehlerfortpflanzung. Die Abweichung der Gesamtmessung errechnen wir durch die
Wurzel der Summe der Fehlerquadrate der Einzelmessungen.
sg =
n
!s
k =1
2
k
Der Absolutfehler ergibt sich durch:
! A = 180 " (# + $ + % )
Winkel α
i
1
2
3
4
5
6
Summe
α
24,92
25,75
26,85
26,85
26,67
26,75
157,79
Δ α2
1,90
0,30
0,30
0,30
0,14
0,20
3,15
Δα
-1,38
-0,55
0,55
0,55
0,37
0,45
0,00
Auswertung der Messdaten
<α> [°]
26,30
s [°]
0,79
sm
0,32
εA[°]
0,79
εR
0,030
Der erste Winkel beträgt 26,30° mit einer Abweichung von 0,79°.
Winkel β
i
1
2
3
4
5
6
Summe
β
58,50
58,42
58,58
58,50
58,83
58,58
351,41
Δβ
-0,07
-0,15
0,01
-0,07
0,26
0,01
0,00
Δβ2
0,00
0,02
0,00
0,00
0,07
0,00
0,10
Seite 12
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Auswertung der Messdaten
<β> [°]
58,57
s [°]
0,14
sm
0,06
εA[°]
0,14
εR
0,242
Der Winkel β ist laut unseren Messungen 58,57 ±0,14°.
Winkel γ
i
1
2
3
4
5
6
Summe
γ
93,25
93,50
93,50
93,42
93,43
93,50
560,60
Δγ2
0,03
0,00
0,00
0,00
0,00
0,00
0,05
Δγ
-0,18
0,07
0,07
-0,01
0,00
0,07
0,00
Auswertung der Messdaten
< γ > [°]
93,43
s [°]
0,10
sm
0,04
εA[°]
0,10
εR
0,001
Der dritte Winkel des Dreieckes beträgt nach unseren Messungen 93,43 ±0,1°.
Die Summe unserer drei Winkel beträgt 178,3°. Damit ist unser absoluter Fehler 1,7°.
Die Standardabweichung welche wir mithilfe der Fehlerfortpflanzung bestimmt haben, ist
s=0,81°.
2.1.3 Dichtebestimmung
In dieser Übung bestimmen wir die Dichte eines Probekörpers dessen Grundfläche, Volumen
und Masse unbekannt sind.
Die Grundfläche wird über Massevergleich ermittelt. Wir schneiden uns zwei
Vergleichskörper zurecht. Einen dessen Fläche (1dm2) wir kennen, und einen dessen Fläche
der des Probekörpers entspricht. Von beiden je drei Stück. Wir ermitteln die Masse der
Probekörper mithilfe einer Feinwaage und stellen folgende Relation auf:
A2 m2
m
=
! A2 = 2 A1
A1 m1
m1
Die Genauigkeit der Feinwaage liegt bei 0,1mg. Die Masse des Probekörpers ist 83,3132g.
Seite 13
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Das Volumen des Körpers wird durch
V = A2 d
bestimmt. Wir messen die Materialstärke d mit einer Mikrometerschraube die eine
Genauigkeit von 0,01mm besitzt.
Durch die verschiedenen Einflussfaktoren entstehen mehrere Messunsicherheiten. Über die
Fehlerfortpflanzung ermitteln wir die relativen Fehler von Fläche, Volumen und Dichte.
2
" !m % " !m 2 %
!A2
= $ 1' + $
'
A2
# m1 & # m2 &
2
" !A % " !d %
!V
= $ 1' +
V
# A1 & # d &
2
!(
" !V % " !m %
=
+
# V & # m&
(
2
2
2
Messwerte der Materialstärke
i
1
2
3
4
5
6
d [mm]
2,45
2,445
2,435
2,46
2,46
2,46
14,71
Δ di
-0,0017
-0,0067
-0,0167
0,0083
0,0083
0,0083
0,0000
Δ d2i
0,0000
0,0000
0,0003
0,0001
0,0001
0,0001
0,0005
Auswertung Materialstärke
<d> [mm]
2,4517
s [mm]
0,0103
sm [mm]
0,0042
εA[mm]
0,0103
εR
0,4201
Das untersuchte Material hat eine mittlere Höhe (Stärke) von h=2,45 ±0,01mm.
Seite 14
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Messergebnisse Masse 1
i
1dm3 [g]
Δ di
Δ d2i
1
2
3
0,5896
0,5843
0,5946
1,7685
0,0001
-0,0052
0,0051
0,0000
0,0000
0,0000
0,0000
0,0001
Auswertung Masse 1
<m> [g]
0,5895
s [g]
0,0052
sm [g]
0,0030
εA[g]
0,0052
εR
0,0088
Das Messergebnis der Wägung des Körpers mit bekannter Fläche von 1dm3 ist anhand unserer
Rechnung
m1= 0,5895 ±0,0052g.
Messergebnisse Masse 2
I
1
2
3
Xdm3 [g]
0,2484
0,2473
0,2532
0,7489
delta di
-0,0012
-0,0023
0,0036
0,0000
delta d2i
0,0000
0,0000
0,0000
0,0000
Auswertung Masse2
<m> [g]
0,2496
s [g]
0,0031
sm [g]
0,0018
εA[g]
0,0031
εR
0,0124
Die Masse des Körpers mit unbekannter Fläche ist
m2= 0,2496 ±0,0031g.
Berechnung der Dichte
Der relative Fehler der Flächen kann nun anhand der oben angegeben Formel berechnet
werden.
!A2
= 1,5232%
A2
Seite 15
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Die Fläche des Probekörpers über den Massenvergleich berechnet ergibt:
A=0,4235 ±0,006dm2.
In Folge ergibt sich der relative Fehler des Volumens durch
!V
= 1,5801%
V
Da nun Fläche und Höhe des Probekörpers bekannt sind, errechnen wir das Volumen
V=0,10382 ±0,00016 dm3.
Der relative Fehler der Waage ist aufgrund deren Genauigkeit von 0,1mg sehr gering, nämlich
0,00012% und macht sich dadurch kaum im relativen Fehler der Dichte bemerkbar.
Wir bestimmen den relativen Fehler der Dichtebestimmung durch
!"
= 1,5801% .
"
Schließlich und endlich berechnen wir die Dichte des Probekörpers.
!=
m
= 8,011 ± 0,13kg /dm 3
V
2.1.4 Erdbeschleunigung
Der Versuch zielt darauf, die Erdbeschleunigung durch die Schwingungsdauer eines
Mathematischen Pendels zu bestimmen. Bei der Durchführung nehmen wir einmal eine
Messreihe mit der Schwingungsdauer jeweils einer Schwingung auf, und darauf eine
Messreihe mit der Schwingungsdauer von 15 Schwingungen. Wir beobachten dabei, wie hoch
der Einfluss des statistischen Fehlers ist. Als wahren Wert für die Gravitation nehmen wir
g=9,81m/s2 an.
g=
4! 2 l
T2
Durch die Fehlerfortpflanzung ergibt sich die Standardabweichung
2
2
' 4( 2 $ 2 ' 8( 2l $
!g = %% 2 "" !l + %% 3 "" !T 2
& T #
& T #
Die Länge des Pendels ist vom Aufhängepunkt bis zum Schwerpunkt l=0,655m. Wir gehen
des Weiteren von einem Ablesefehler von rund 0,002m aus.
Seite 16
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Wir tauschen am Schluss die Messergebnisse von Länge und Schwingungsdauer mit den
anderen Übungsgruppen aus, und ermitteln die lineare Regression mit Hilfe von Origin.
Messwerte für 1 Schwingung
I
1
2
3
4
5
6
7
8
9
10
1 Schwing
[s]
1,74
1,70
1,49
1,64
1,63
1,64
1,68
1,66
1,71
1,66
16,55
Δs2
0,01
0,00
0,03
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,04
Δsi
0,08
0,04
-0,17
-0,02
-0,03
-0,02
0,02
0,00
0,05
0,00
-0,09
Auswertung bei einer Schwingung
<t> [sec]
1,6550
s [sec]
0,0718
sm
0,0227
Δg [sec]
Δgrel [%]
0,819
8,68
Die mittlere Periode ist
T=1,655 ±0,0718 sek.
Der Abweichung anhand der Fehlerfortpflanzung ergibt
Δg=0,819m/s2.
Die Erdbeschleunigung ist also laut unserer ersten Messreihe
=9,441 ± 0,819m/s2.
Unsere Abweichung vom Literaturwert beträgt:
ε= 0,369m/s2.
Seite 17
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Messergebnisse bei 15 Schwingungen
I
1
2
3
4
5
6
7
8
9
10
15 Schwing [s]
23,70
23,78
24,50
24,59
24,59
24,74
24,63
23,30
24,62
23,81
242,26
Δs2
0,28
0,20
0,08
0,13
0,13
0,26
0,16
0,86
0,16
0,17
2,43
Δs
-0,53
-0,45
0,27
0,36
0,36
0,51
0,40
-0,93
0,39
-0,42
0,54
Auswertung für 15 Schwingungen
<t> [sec]
24,2260
s [sec]
0,5287
sm
0,1672
Δg [sec]
Δgrel [%]
0,434
4,38
Eine Schwingung dauert damit
T=1,615 ±0,035m/s2.
Durch Anwendung der Fehlerfortpflanzung erhalten wir die Abweichung von
Δg=0,434m/s2.
Die berechnete Erdbeschleunigung ist damit
g=9,913 ± 0,434m/s2.
Die Abweichung vom Literaturwert beträgt jetzt:
ε= -0,103m/s2.
Seite 18
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Lineare Regression
Die unterschiedlichen Werte der Pendellänge und Schwingungsdauer sowie ihre
Abweichungen werden in Origin ausgewertet um eine Ausgleichsgerade zu errechnen.
Aus dem B-Wert (Diagramm) kann somit auch g ermittelt werden. Der Anstieg zwischen L
und T² besteht aus dem reziproken Wert von g und zusätzlichen Konstanten. Dies Konstanten
muss man aus der Steigung rausbekommen und außerdem muss man vom reziproken auf den
normalen Wert wechseln. Daraus folgt, dass man den B-Wert folgendermaßen korrigieren
muss:
4" 2
4" 2
4" 2
T = B!l =
!l # B =
#g=
= 10,16ms$2
g
g
B
2
Seite 19
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.2 Messaufgaben Teil 2 – Elektrische Messungen
2.2.1 Genauigkeit elektrischer Messungen
Um die Genauigkeit elektrischer Messungen feststellen zu können, soll der Widerstand
mittels Strom- und Spannungsmessung ermittelt werden (mittels Ohm’schem Gesetz).
Hierzu werden analoge und digitale Vielfachmessgeräte (Multimeter) eingesetzt. Sie sind auf
mehrere Spannungs- und Strommessbereiche umschaltbar.
Es ist wichtig, dass der Messbereich so gewählt wird, dass das Messgerät nicht überlastet.
Die Messungenauigkeit des analogen Geräts über einen prozentuellen Wert des
Skalenendwerts gegeben ist. Hier sieht man auch, dass es wichtig ist, den Bereichs-Endwert
möglichst nahe an dem gemessenen Wert zu haben, weil es ansonsten einen viel größeren
Fehler gibt. Jedoch sollte man den Bereich am Anfang möglichst hoch wählen, um eine
Überlastung zu vermeiden und schaltet dann schrittweise auf einen genaueren Bereich.
Bei Digitalmessgeräten gibt es zur Anzeige ein digitales Display und der Messfehler hängt
hauptsächlich von der Auflösung dieses Displays ab.
Ein Messgerät zur Spannungsmessung muss parallel zur Spannungsquelle oder Widerstand
geschaltet werden und zwar aufgrund der Kirchhoff’schen Regeln und des Ohm’schen
Gesetzes (welche später noch ausführlicher erklärt werden) und auch wegen des hohen
Innenwiderstandes von Spannungsmessgeräten (es würde fast die komplette Spannung bereits
an dem Messgerät abfallen und kaum welche mehr durch den Stromkreis laufen).
Ein Messgerät zur Strommessung muss in Serie mit dem Stromkreis eingefügt werden, auch
aufgrund der Kirchhoff’schen Regeln und des Ohm’schen Gesetzes und um einen
Kurzschluss aufgrund des niedrigen Innenwiderstands zu vermeiden.
2.2.2 Messungen mit Gleichspannung
2.2.2.1 Grundlagen: Ohm’sches Gesetz, Leistung, Kirchhoff’sche Regeln
Zur Bestimmung des Widerstands wird das Ohm’sche Gesetz verwendet. Es wird die
Spannung U und die Stromstärke I ermittelt und daraus mittels des Ohm’schen Gesetzes der
Widerstand R. Wobei der Widerstand R auch durch einen Verbraucher wie eine Lampe
gegeben sein kann. Es ist vollkommen egal, was den Widerstand verursacht, weswegen
Schaltbilder häufig den Verbraucher einfach als Widerstandssymbol kennzeichnen:
I
U
R
Seite 20
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Das Ohm’sche Gesetz besagt folgendes:
I=
U
R
Wenn man die Formel auf R umformt und U in Volt (V) und I in Ampere (A) einsetzt so
erhält man R in Ohm (Ω).
Die verbrauchte Leistung in einem Gleichstromkreis ergibt sich zu:
P = IU
Wird U in V und I in A eingesetzt so erhält man P in Watt (W).
Wenn zwei oder mehrere geschlossene Stromkreise (Maschen) durch Knotenpunkte
verbunden sind (parallel geschaltete Verbraucher), teilt sich der Strom auf:
I
I1
U
R1
I2
R2
Seite 21
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Es gilt hier das erste Kirchhoff’sche Gesetz – Knotenregel:
In einem Knotenpunkt ist die Summe aller Ströme gleich Null, wobei alle einfließenden
Ströme mit positiven Vorzeichen sind und die ausfließenden mit negativem Vorzeichen:
!I
k
=0
k
Wenn in einem Stromkreis mehrere Verbraucher und Spannungsquellen in Serie geschaltet
werden, dann werden diese alle vom gleichen Strom (I) durchflossen. Es liegt jedoch an
jedem Verbraucher eine andere Spannung an, diese bezeichnet man als Spannungsabfall am
jeweiligen Verbraucherwiderstand:
I
U1
R1
+
-
R2
U2
IR1
IR2
+
-
R3
IR3
Es gilt das zweite Kirchhoff’sche Gesetz – Maschenregel:
Die Summe über alle Quellenspannungen und alle Spannungsabfälle an den
Verbraucherwiderständen ist in einer geschlossenen Masche (Stromkreis) gleich Null.
Quellenspannungen sind stets vom Plus- zum Minuspol gerichtet, die technische
Stromrichtung verläuft vom Plus zum Minuspol und die einzelnen Spannungsabfälle haben
dieselbe Richtung wie die Stromstärke:
!U + ! I R
k
k
k
=0
k
Der einfachste Fall ist ein Spannungsteiler (Potentiometer):
Hier gibt es einen Stromkreis mit einer Spannungsquelle und zwei Widerständen:
Seite 22
Anfängerpraktikum 1 - PW1
Allacher & Krieger
I
R1
U1
U
R2
U2
Aufgrund des zweiten Kirchhoff’schen Gesetzes folgt:
I=
U1 U 2
=
R1 R2
und
U1 =
UR1
( R1 + R2 )
Aus dem zweiten Kirchhoff’schen Gesetz folgt außerdem, dass in Serie geschaltete
Widerstände einen Gesamtwiderstand ergeben, dessen Wert gleich der Summe der
Einzelwiderstände ist:
Rg = ! Ri
i=1
Durch Anwendung der Kirchhoff’schen Gesetze lässt sich auch der Gesamtwiderstand für
parallel geschaltete Widerstände bestimmen und zwar ist der Reziprokwert des
Gesamtwiderstands gleich der Summe der einzelnen Widerstandsreziprokwerte:
1
1
=!
Rg
k Rk
Zur Spannungsmessung wird das Messgerät parallel zum Widerstand R und zur
Strommessung in Serie zum Widerstand R geschaltet. Bei der Spannungsmessung
(Parallelschaltung) entsteht ein neuer Knotenpunkt und es fließt ein (minimaler) Strom ab.
Bei hohem Innenwiderstand des Messgeräts fließt wenig Strom ab, wenn er genügend hoch ist
kann dieser vernachlässigt werden.
Bei der Strommessung fällt eine (minimale) Spannung ab, da das Messgerät ein weiterer
Verbraucher ist. Dieser Spannungsabfall ist bei niedrigem Innenwiderstand klein und kann
bei entsprechend niedrigem Widerstand vernachlässigt werden.
Zur Bestimmung eines unbekannten Widerstands werden Strom und Spannung mittels zweier
Messgeräte gleichzeitig gemessen. Hier kann entweder „spannungsrichtig“ (es wird nur die
Spannung gemessen die am Widerstand tatsächlich anliegt) oder „stromrichtig“ (es wird nur
der Strom gemessen der am Widerstand tatsächlich anliegt) gemessen werden.
Seite 23
Anfängerpraktikum 1 - PW1
Allacher & Krieger
A
U
A
V
a) „spannungsrichtig“
R
U
V
R
b) „stromrichtig“
In Schaltung a) wird die Spannung am Widerstand richtig gemessen, jedoch fließt ein Teil des
mittels des Amperemeters (in der Zeichnung A; Messgerät für I) gemessenen Stroms noch
über das parallel geschaltete Spannungsmessgerät (in der Zeichnung V; wird auch als
Voltmeter bezeichnet) ab. Wird dieser Teilstrom bei der Berechnung des Widerstands R nicht
berücksichtigt, so könnte dies zu einem systematischen Fehler bei dem zu bestimmenden
Wert von R führen. Dieser Teilstrom ist dann zu vernachlässigen, wenn der Innenwiderstand
des Voltmeters groß gegen R ist.
In Schaltung b) wird der Strom durch R richtig gemessen, jedoch misst das Voltmeter den
Spannungsabfall der in Serie geschalteten Verbraucher (Widerstand und Amperemeter). Der
Spannungsabfall des Amperemeters ist nur dann vernachlässigbar, wenn der Innenwiderstand
klein gegen R ist.
Die Innenwiderstände der Messgeräte hängen vom gewählten Messbereich ab.
Diese sind für die Spannungsbereiche direkt in Ω angegeben, müssen sie bei den
Strommessbereichen meist aus dem Spannungsabfall beim Messendwert berechnet werden.
2.2.2.2 Widerstand und Leistung einer Glühlampe („stromrichtig“ und „spannungsrichtig“)
2.2.2.2.1 Beschreibung
Der Ohm’sche Widerstand und die Leistung einer Glühlampe soll ermittelt werden. Dies soll
sowohl mit einer „spannungsrichtigen“ und einer „stromrichtigen“ Schaltung geschehen. Das
Analoginstrument soll als Voltmeter im 30V-Bereich verwendet werden. Das Digitalgerät soll
als Amperemeter verwendet werden und dieses wählt sich den besten Bereich selbst aus.
Für beide Messungen ist die Innenwiderstandskorrektur durchzuführen und der Fehler des
errechneten Innenwidertands auf Grund der Messungenauigkeit der Instrumente zu
bestimmen. Außerdem soll festgestellt werden, ob die Innenwiderstandskorrektur, verglichen
mit dem Messfehler, wesentlich oder vernachlässigbar ist.
Für die Innenwiderstandkorrektur ergeben sich folgende Formeln:
a) „spannungsrichtig“:
Man muss den Strom korrigieren und zwar um jenen Strom der durch das Messgerät
fließt.
Dies bedeutet die gemessene Spannung durch den Innenwiderstand des Voltmeters
ergibt den Wert um welchen der Strom korrigiert werden muss.
Seite 24
Anfängerpraktikum 1 - PW1
Allacher & Krieger
I Korr =
UV
RI (v )
IKorr ...... Strom durch das Voltmeter (zu korrigierender Strom)
UV ........ am Voltmeter gemessene Spannung
RI(V)...... Innenwiderstand des Voltmeters
Aufgrund des erstens Kirchhoff’schen Gesetzes muss die Summe aller Ströme gleich
Null sein, daraus folgt:
IWid = I Gem ! I Korr
IWid ....... durch den Widerstand fließender Strom
IGem ...... gemessener Strom
IKorr ...... Strom durch das Voltmeter (zu korrigierender Strom)
b) „stromrichtig“:
RI ( A) =
U Max
I Max
RI(A)...... Innenwiderstand des Amperemeters
UMax ..... maximaler Spannungsabfall beim Bereichsendwert
IMax....... Maximale Stromstärke des Bereichs (Bereichsendwert)
U A = RI ( A) ! I Gem
UA ........ abgefallene Spannung am Amperemeter
IGem ...... gemessener Strom
RI(A)...... Innenwiderstand des Amperemeters
UWid = U Gem ! U A
UWid ..... am Widerstand abfallende
UGem ..... gemessene Spannung
UA ........ am Amperemeter abfallende Spannung
2.2.2.2.2 Messungen und Berechnungen
Geräte: Unigor 1n (analog): Spannung im 30V-Bereich: Innenwiderstand RI = 100kΩ
Fehler: 1,0 % vom Bereichsendwert
FLUKE 183 (digital): Strom im 50mA-Bereich:
von 5mA bis 5A: 0,3V max. Spannungsabfall
Genauigkeit: ± 0,2 % + 4 Zählimpulse
oI............ ohne Innenwiderstandkorrektur
mI........... mit Innenwiderstandkorrektur
Seite 25
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Fehlerfortpflanzung:
Ohmsches Gesetz, relativer Fehler:
2
'R
& 'U # & 'I #
= $
! +$ !
R
% U " % I "
2
Standardabweichung:
' ' (U $ 2 ' (I $ 2 $
"!R
(R = % %
+
% & U "# %& I "# "
&
#
Leistung, relativer Fehler:
2
'P
& 'U # & 'I #
= $
! +$ !
P
% U " % I "
2
Standardabweichung:
' ' (U $ 2 ' (I $ 2 $
"! P
(P = % %
+
% & U "# %& I "# "
&
#
Korrekturstrom, relativer Fehler:
& 'UV
'I Korr
= $$
I Korr
% UV
2
# & 'RI (V ) #
!
!! + $
$ R
!
" % I (V ) "
2
Standardabweichung:
(I Korr
'
%
=%
%
&
' (U V
%%
& UV
2
$ ' (RI (V ) $
"
"" + %
%
"
# & RI (V ) #
2
$
"
" ! I Korr
"
#
Korrigierter Strom, Standardabweichung:
2
!IWid = !I Gem + !I Korr
2
Korrekturspannung, relativer Fehler:
!U A !I Gem
=
!U
I Gem
Seite 26
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Standardabweichung:
!U A =
!I Gem
" !U
I Gem
Korrigierte Spannung, Standardabweichung:
2
!U Wid = !U Gem + !U A
2
Messergebnisse
Art
Spannungsrichtig
rel. Fehler (in %)
Standardabw.
Stromrichtig
rel. Fehler (in %)
Standardabw.
Korr. (U oder I)
0,24
1,78
0,004270
0,0009018
0,20
0,000002
U [V]
24
1,25
0,3
24
1,25
0,3
Korr. Wert
15
0,21
0,0312
23,9999991
1,25
0,3
I [mA]
15,24
0,202624672
0,03088
15,03
0,202661344
0,03046
Korr.: U oder I?
[Einheit]
I [mA]
I [mA]
I [mA]
U [V]
U [V]
U [V]
R (oI) [Ω]
1574,80
1,27
19,94
1596,81
1,27
20,22
R (mI) [Ω]
1600
2,17
34,79
1596,81
1,27
20,22
P (oI) [mW]
365,76
1,27
4,63
360,72
1,27
4,57
P (mI)
[mW]
360
2,17
7,83
360,72
1,27
4,57
Diskussion (bzw. für die nächsten Beispiele):
Die Innenwiderstandskorrektur ist bei der stromrichtigen Schaltung mit digitalem
Amperemeter prinzipiell vernachlässigbar, kaum eine Änderung des Wertes und der
statistische Fehler ändert sich noch weniger. Bei der „spannungsrichtigen“ Schaltung mit
analogem Voltmeter macht es einen größeren Unterschied, ob die Innenwiderstandskorrektur
angewandt wird oder nicht. Dies liegt aber hauptsächlich an dem analogen Messgerät, da der
Innenwiderstand nicht so hoch ist, wie beim digitalen Messgerät. Außerdem kommt es
aufgrund der Fehlerfortpflanzung zu einer Erhöhung des Fehlers nach der
Innenwiderstandskorrektur.
Es wurde festgestellt, dass wenn man eine „stromrichtige“ Messung durchführt, die
Innenwiderstandkorrektur vernachlässigt werden kann. Dies hängt mehr mit dem digitalem
Messgerät zusammen als mit der Art der Messung.
Da der Strom jedoch bereits ziemlich niedrig ist, ist es nicht so wichtig diesen so extrem
genau zu messen und deswegen wäre es sinnvoller „spannungsrichtig“ zu messen und dafür
jedoch das digitale Messgerät als Voltmeter zu verwenden und das analoge Messgerät für die
Strommessung.
Dies wird bei den kommenden Messungen wo Strom und Spannung zur selben Zeit gemessen
werden so angewandt (also „spannungsrichtig“ mit digitalem Messgerät als Voltmeter und
analogem Messgerät als Amperemeter).
Seite 27
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.2.2.3 Bestimmung eines Metallfilmwiderstandes
Es wird aufgrund dessen, was bei der Diskussion im vorigen Beispiel erwähnt wurde, das
analoge Messgerät als Amperemeter und das digitale als Voltmeter verwendet. Aus diesem
Grund verwenden wir für den Versuchsaufbau eine spannungsrichtige Schaltung.
Formeln für Fehlerfortpflanzung beim vorigen Beispiel nachschauen, das analoge Messgerät
wurde im 12mA-Bereich verwendet und das digitale ermittelt den Bereich automatisch (und
kam somit auf den 50V-Bereich).
Die Innenwiderstandkorrektur kann aufgrund dieser Kombination vernachlässigt werden.
Art
Spannungsrichtig
rel. Fehler (in %)
Standardabw.
U [V]
23,970
0,112
0,027
I [mA]
4,050
2,963
0,120
R [Ω]
5918,519
2,965
175,488
2.2.2.4 Spannungsteiler
Es ist ein Spannungsteiler aus einem bekannten und dem unbekannten Widerstand
(Metallfilmwiderstand aus 2.2.2.3) aufzubauen.
Durch Messung der Teilspannungen soll der unbekannte Widerstand ermittelt werden.
Außerdem soll noch der Messfehler ermittelt werden, wenn der bekannte Widerstand
vernachlässigbar klein ist.
I
R1
U1
U
R2
U2
R1 ........... unbekannter Widerstand
U2 ........... Spannungsabfall am unbekanntem Widerstand
R2 ........... bekannter Widerstand
U2 ........... Spannungsabfall am bekanntem Widerstand
Die Teilspannungen werden beide mit dem digitalem Messgerät FLUKE 183 nach der Reihe
ermittelt (zuerst U1 danach U2). Der Bereich wird wieder automatisch ermittelt (für beide
Teilspannungen wurde hier der 50V-Bereich ermittelt).
Der unbekannte Widerstand R1 lässt sich folgendermaßen ermitteln:
Zuerst wird der Strom I der Schaltung berechnet:
Seite 28
Anfängerpraktikum 1 - PW1
Allacher & Krieger
I=
U2
R2
Damit kann der Widerstand R1 ermittelt werden:
R1 =
U1
I
Daraus folgt für den Widerstand R1:
R1 =
U1 ! R2
U2
Fehlerfortpflanzung:
Relativer Fehler von I:
2
2 #
&
'I $ & 'U 2 # & 'R2 # !
! +$
!
= $ $$
I
$ % U 2 !" $% R2 !" !!
%
"
Standardabweichung von I:
'
%
(I = %
%
&
2
2
' (U 2 $ ' (R2 $ $"
%%
"" + %%
"" " ! I
& U 2 # & R2 # "#
Relativer Fehler für R1:
2
2
& 'U1 # & 'U 2 # & 'R2 #
'R1
!! + $$
!! + $$
!!
= $$
R1
% U1 " % U 2 " % R2 "
2
Standardabweichung von R1:
'
%
(R1 = %
%
&
2
2
2
' (U1 $ ' (U 2 $ ' (R2 $ $"
%%
"" + %%
"" + %%
"" " ! R1
U
U
R
& 1 # & 2 # & 2 # "#
Da R2 mit einem vernachlässigbar kleinen Fehler behaftet sein soll:
Relativer Fehler von I:
!I !U 2
=
I
U2
Standardabweichung von I:
' (U 2 $
"" ! I
(I = %%
U
2
&
#
Seite 29
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Relativer Fehler für R1:
2
& 'U1 # & 'U 2 #
'R1
!! + $$
!!
= $$
R1
% U1 " % U 2 "
2
Standardabweichung von R1:
'
%
(R1 = %
%
&
2
2
' (U1 $ ' (U 2 $ $"
%%
"" + %%
"" " ! R1
U
U
& 1 # & 2 # "#
Messergebnisse
Art
Spannungsrichtig
rel. Fehler (in %)
Standardabw.
U1 [V]
13,450
0,144
0,019
U2 [V]
10,550
0,165
0,017
R2 [Ω]
4700
I [mA]
2,245
0,165
0,000
R1 [Ω]
5991,943
0,145
8,706
2.2.2.5 Gesamtwiderstand - Seriell, Parallel
Es ist der Gesamtwiderstand sowohl einer Serienschaltung als auch einer Parallelschaltung zu
aus bekanntem und unbekanntem Widerstand zu messen. Und zu überprüfen ob der Wert des
Gesamtwiderstands innerhalb der Fehlergrenzen mit dem errechnetem Wert aus den
Einzelwiderständen übereinstimmt. Hierzu soll der Fehler des bekannten Widerstands (R2)
vernachlässigt werden.
a) Serienschaltung:
Hier wird 2.2.2.4 fortgesetzt indem der Gesamtwiderstand gemessen wird
(Spannungsmessung mit FLUKE 183 – Bereich automatisch gewählt; je 50V-Bereich
ermittelt - und Strommessung mit Unigor 1n – 3mA-Bereich) und der
Gesamtwiderstand auch rechnerisch ermittelt wird.
Hierzu wird
Rg = ! Ri
i=1
verwendet. Daraus folgt für das Beispiel:
Rg = R1 + R2
Da der Fehler von R2 zu vernachlässigen ist, ist der Fehler des errechneten
Gesamtwiderstands gleich dem Fehler von R1.
Seite 30
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Für den Fehler des gemessenen Gesamtwiderstands gilt:
Relativer Fehler für Rg:
'Rg
Rg
& 'U g
= $
$ U
% g
2
# & 'U 2 #
! +$
!
! $ U !
2
%
"
"
2
Standardabweichung von Rg:
'
%
(Rg = %
%
&
' (U g
%
% U
& g
2
2
$ ' (U 2 $ $"
" +%
" !R
" % U " "" 1
2
&
#
#
#
Messergebnisse
Art
U1
[V]
U2
[V]
Ug
[V]
R2
[Ω]
I1
[mA]
Ig
[mA]
R1 [Ω]
Rg [Ω]
Rg [Ω]
(errechnet)
Spannungsrichtig
13,450
10,550
24,000
4700
2,245
2,250
5991,943
10666,667
10691,943
rel. Fehler (in %)
0,144
0,165
0,112
0,165
0,013
0,145
1,338
0,145
Standardabw.
0,019
0,017
0,027
0,000
0,030
8,706
142,720
8,706
b) Parallelschaltung:
Die Schaltung sieht jetzt folgendermaßen aus:
I
I1
U
R1
I2
R2
R2 ist bereits bekannt und der Fehler vernachlässigbar klein.
R1 und Rg wird mittels des Ohm’schen Gesetzes ermittelt. Die Formeln für die
Fehlerfortpflanzung dafür wurden bereits in 2.2.2.2.2 ermittelt. Die Messung von U
und I erfolgt mittels derselben Gerätkonfiguration wie sie bei 2.2.2.3 verwendet wurde
(und auch die Bereichswahl ist dieselbe).
Der errechnete Gesamtwiderstand wird ermittelt mittels:
1
1
=!
Rg
k Rk
Seite 31
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Daraus folgt:
Rg =
R1 ! R2
R1 + R2
Fehlerfortpflanzung für Rg für vernachlässigbar kleinen Fehler von R2:
2
( R1 %
## " !R1
!Rg = &&
' R1 + R2 $
Messergebnisse
Art
Spannungsrichtig
rel. Fehler (in %)
Standardabw.
Ug
[V]
Ig
[mA]
U1
[V]
I1
[mA]
9,15
1,31
Rg [Ω]
2620,77
1,32
24,00
0,11
4,05
2,96
R1 [Ω]
5925,93
2,97
23,98
0,11
0,03
0,12
34,50
0,03
0,12
175,71
R2 [Ω]
4700,00
Rg [Ω]
(errechnet)
2621,12
2,08
54,65
2.2.3 Spannungsteiler bei Wechselstrom
2.2.3.1 Grundlagen zur Bestimmung elektrischer Wechselstromwiderstände
Zusätzlich zum Ohm’schen Widerstand kann es beim Wechselstrom auch kapazitiven und
induktiven Widerstand geben. Der kapazitive Widerstand entsteht z.B. durch das elektrische
Feld eines Kondensators und der induktive durch das magnetische Feld einer Spule.
Für Wechselstromwiderstände ist das ohm’sche Gesetz nicht direkt anwendbar, denn:
1) hängen die Widerstandswerte von der Frequenz des Wechselstroms ab.
2) kommt es an induktiven und kapazitiven Widerständen zu einer Phasenverschiebung
zwischen Strom und Spannung (keine gleichzeitigen Maxima und Minima).
Zur Berechnung verwendet man deswegen einen mathematischen Trick und zwar verwendet
man die komplexen Zahlen für die Widerstände.
Der ohm’sche Widerstand wird als Realteil der komplexen Zahlen und der kapazitive und
induktive der Imaginärteil aufgefasst. Dies ist aufgrund der Euler-Relation zwischen Sinus,
Cosinus und der eulerschen Zahl e möglich.
Diese komplexen Widerstände werden als Impedanz bezeichnet und diese werden
üblicherweise mit dem Buchstaben Z symbolisiert (zur Unterscheidung vom ohm’schen
Widerstand R).
In der Elektrizitätslehre wird j für die imaginäre Einheit (und nicht i) verwendet um eine
Verwechslung mit dem Strom zu vermeiden; j = ! 1
Seite 32
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Für den kapazitiven Widerstand gilt:
Zc =
"j
wobei
# !C
Zc =
1
" !C
C ..........Kapazität in Farad [F]
ω ..........Kreisfrequenz (ω=2πf)
Für den induktiven Widerstand gilt:
Z L = j!L wobei
Z L = !L
L...........Induktivität in Henry [H]
Verwendet man die komplexe Darstellung für kapazitive und induktive Widerstände, so
gelten für die komplexen Impedanzen das Ohm’sche Gesetz und die Kirchhoff’schen Regeln
in gewohnter Form.
Die verwendete Wechselspannung wird mittels eines Transformators aus dem Stromnetz
erzeugt und hat daher dieselbe Frequenz wie die Netzwechselspannung (50Hz).
2.2.3.2 Kapazität C aus Spannungsteiler ermitteln
Es soll die Kapazität C mittels Spannungsteiler ermittelt werden.
Hierzu wird folgende Schaltung verwendet:
I
R
UR
U
C
UC
Es wird der Spannungsabfall an den beiden Teilwiderständen gemessen, jedes Mal mit
FLUKE 183.
Aus dem rein ohm’schen Widerstand R lässt sich die Stromstärke I ermitteln.
Damit kann man mittels des ohm’schen Gesetzes und der Impedanz der Kapazität (hier wird
nur der Betrag
Zc =
1
" !C
benötigt, da man die Kapazität haben will) die Kapazität C ermittelt werden.
Seite 33
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Es ergibt sich:
C=
I
UC "!
Der Fehler von der Kreisfrequenz und des bekannten Widerstands ist vernachlässigbar.
Dadurch ist der relative Fehler von I gleich dem relativen Fehler vom Spannungsabfall UR des
ohm’schen Widerstands.
Der relative Fehler von C:
2
'C
& 'I # & 'U C
= $ ! + $$
C
% I " % UC
#
!!
"
2
Die Standardabweichung von C:
2
'
% ' (I $ '% (U C
(C = % % " + %
% & I # & UC
&
$
""
#
2
$
"
"" ! C s
#
Messergebnisse
Art
Ohm mit Rx
Kapazität
Ug [V]
27,21
27,24
U1 [V]
11,96
8,69
U2 [V]
15,23
25,79
Seite 34
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.2.3.3 Grafischer Zusammenhang zwischen Wechselstromspannungen
Ersetzt man die Kapazität beim Spannungsteiler durch den in 2.2.2.3 bestimmten Widerstand
Rx, so erhält man einen rein ohm’schen Spannungsteiler im Wechselstromkreis.
Der Zusammenhang der Teilspannungen U1 und U2 mit der Gesamtspannung U ist für beide
Fälle darzustellen – R in Serie mit Rx und R in Serie mit ZC grafisch darzustellen.
Seite 35
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.3 Messaufgaben Teil 3
2.3.1 U0 und Ri einer realen Stromquelle
2.3.1.1 Grundlagen
Schaltet man an den Klemmen einer Spannungsquelle einen Verbraucher, so erhält man den
einfachsten Stromkreis, den Grundstromkreis. Die reale Spannungsquelle stellt man im
Ersatzschaltbild durch die Serienschaltung einer idealen Spannungsquelle (Quellenspannung)
U0 und einem Innenwiderstand RI dar.
Die Größe des Innenwiderstandes hängt von der speziellen Art und dem Aufbau der
Spannungsquelle ab.
Schaltungsbild:
K+
I
U0
U
Ui
Ra
Ri
K+, K-.......Anschlussklemmen
U0..............Quellenspannung
U...............Klemmenspannung
Ri ..............Innenwiderstand
Ra ..............Belastungswiderstand
I ................Stromstärke
KUnter Anwendung des Ohm’schen Gesetzes und der Kirchhoff’schen Regeln ergibt sich für
die Klemmenspannung:
U = U 0 ! IRi
Man sieht dass die Klemmenspannung bei Belastung stets kleiner ist als die Quellenspannung.
An den Klemmen liegt nur dann die Quellenspannung an, wenn kein Strom fließt (I = 0A).
Daraus folgt für den Innenwiderstand
Ri =
U0 !U
I
Seite 36
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.3.1.2 Durchführung
Es soll die Strom-Spannungskennlinie (Belastungskennlinie) einer Batterie gemessen werden.
Der Innenwiderstand und die Quellenspannung (sind durch die Strom-Spannungskennlinie)
sind zu bestimmen.
Hierzu wird die Leerlaufspannung gemessen, der Belastungskreis bleibt dabei offen.
Daraufhin sollen verschiedene Klemmenspannungen und Ströme I mit Digitalmultimetern
gleichzeitig gemessen werden:
Hierzu wird ein einstellbarer Widerstand verwendet. Durch verstellen des Widerstandes kann
man verschieden Ströme und Klemmenspannungen messen. Diese kann man dann zum
Ermitteln des Innenwiderstands und der Belastungslinie verwenden.
Da sich die Batterie bei Belastung sollen die Werte schnell gemessen werden und der
Stromkreis daraufhin sofort wieder unterbrochen, da man ansonsten verfälschte Ergebnisse
erhält. Nach den Belastungen soll jeweils wieder die Leerlaufspannung gemessen werden.
Solange sich der Innenwiderstand der Batterie nicht ändert, ergibt sich ein linearer
Zusammenhang zwischen Stromstärke und Spannung. Aus diesem Anstieg der (U,I) –
Geraden kann man den Innenwiderstand Ri bestimmen.
Die Extrapolation der Geraden auf I=0 liefert meist nicht die ursprünglich gemessene
Leerlaufspannung, da die Leerlaufspannung einer Batterie durch die Belastung sinkt
(Änderung des chemischen Gleichgewichts an den Elektroden). Nach genügend langer
Wartezeit kann sich wieder der ursprüngliche Wert einstellen.
Seite 37
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.3.1.4 Messungen und Diagramme
Messung
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
U0 [V]
1,62
1,62
1,62
1,62
1,62
1,62
1,62
1,62
1,62
1,62
1,62
1,62
1,619
1,619
1,618
U [V]
1,618
1,618
1,617
1,614
1,613
1,611
1,607
1,595
1,58
1,575
1,568
1,556
1,548
1,537
1,517
I [µA]
397,7
529
789
1536
1890
2470
3556
3853
15660
19410
25600
37820
50030
73200
139700
Aus der Strom-/Spannungskennlinie (des linearen Verlaufs) ergibt sich ein Innenwiderstand
von
Ri = 3,54 Ω
Seite 38
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.3.2 Belasteter Spannungsteiler
2.3.2.1 Grundlagen
Von einer vorgegebenen Spannung U soll nur ein Teil UL zum Betrieb irgendwelcher
Verbraucher (Lastwiderstände RL) herangezogen werden.
Dazu bedient man sich folgender Schaltung:
I
R-R1
RL
U
R1
I1
UL
IL
Die Spannung U fällt an einem Widerstand R ab, der als Regelwiderstand ausgebildet ist,
sodass ein variabler Teilwiderstand R1 abgegriffen werden kann.
Der Gesamtstrom I verzweigt sich an der Abgreifstelle in einen Teil, der über den
Teilwiderstand R1 fließt und einen Teil, der über den Lastwiderstand RL fließt. Nach dem 1.
Kirchhoff’schen Gesetz gilt also:
I = I1 + I L
Für jeden dieser Ströme gilt das Ohm’sche Gesetz, sodass weiters folgt:
U ! UL UL UL
=
+
R ! R1
R1 RL
Durch Umformung erfolgt daraus:
UL
R1 RL
=
U
RL R + R1 ( R ! R1 )
Kürzt man durch R², so ergibt sich mit den dimensionslosen Bezeichnungen
r1 =
R1
R
und
rL =
RL
R
das Spannungsverhältnis:
Seite 39
Anfängerpraktikum 1 - PW1
Allacher & Krieger
UL
r1rL
=
U rL + r1 (1! r1 )
Das heißt, das Verhältnis der Teilspannung zur Gesamtspannung ist durch das Verhältnis der
Widerstände gegeben.
2.3.2.2 Aufgabe
Für die beigegebenen Lastwiderstände A, B, C ist die Funktion
UL
U
in Abhängigkeit von r1 für mindestens 10 verschiedene Werte von r1 zu ermitteln und
graphisch darzustellen.
Für einen r1 - Wert der möglichst der größten Abweichung vom linearen (unbelasteten)
Verlauf) entspricht ist mit
UL
r1rL
=
U rL + r1 (1! r1 )
der jeweilige Lastwiderstand zu bestimmen. Der Gesamtwiderstand des Potentiometers ist am
Potentiometer angegeben.
Und außerdem ist folgende Frage zu beantworten: Bei welchem r1 tritt die größte
Abweichung vom linearen Verlauf auf,
a) im Grenzfall sehr großer Lastwiderstände
b) im Grenzfall sehr großer Lastwiderstände?
2.3.2.3 Durchführung
U und UL werden mit 2 Voltmetern gemessen. Das Verhältnis r1 ist am Drehpotentiometer
unmittelbar abzulesen (die erste Stelle hinter dem Komma im kleinen Sichtfenster oben –
Anzeige springt nach jeder vollen Umdrehung um 1 weiter), die nächsten beiden Stellen an
der drehbaren Skala.
Zum Errechnen von RL wird die Formel wie folgt umgeformt:
RL =
r1 ! (1 " r1 ) ! U L U
!R
r1 " U L U
Seite 40
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.3.2.4 Messungen und Diagramme
Belasteter Spannungsteiler mit Lastwiderstand A
R [Ω]
UL/U
0,0058
0,1019
0,1911
0,2781
0,3634
0,4520
0,5439
0,6428
0,7491
0,8702
1,0000
r1
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
UL
0,0469
0,824
1,546
2,25
2,94
3,657
4,4
5,2
6,06
7,04
8,09
RL berechnet über r1 mit größter
r1
UL/U
RL
Abweichung von linearen Verlauf
0,7
0,6428
23585,31
10000
U
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
Belasteter Spannungsteiler mit Lastwiderstand B
R [Ω]
10000
RL berechnet über r1 mit größter
Abweichung von linearen Verlauf
UL/U
0,0061
0,0962
0,1763
0,2511
0,3248
0,4017
0,4858
0,5817
0,6922
0,8307
1,0000
r1
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
UL
0,0495
0,778
1,426
2,031
2,628
3,25
3,93
4,706
5,6
6,72
8,09
r1
0,7
UL/U
0,5817
RL
10326,6458
U
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
Seite 41
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Belasteter Spannungsteiler mit Lastwiderstand C
R [Ω]
10000
RL berechnet über r1 mit größter
Abweichung von linearen Verlauf
UL/U
0,0006
0,0870
0,1519
0,2099
0,2658
0,3260
0,4054
0,4850
0,5984
0,7602
1,0000
r1
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
UL
0,0048
0,704
1,229
1,698
2,15
2,637
3,28
3,924
4,841
6,15
8,09
r1
0,7
UL/U
0,4850
RL
4738,59
U
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
8,09
Spannungsverlaufsdiagramm mit Lastwiderstand A,B und C
Seite 42
Anfängerpraktikum 1 - PW1
Allacher & Krieger
2.3.2.5 Diskussion
Bezüglich der Frage: Bei welchem r1 tritt die größte Abweichung vom linearen Verlauf auf,
a) im Grenzfall sehr großer Lastwiderstände
b) im Grenzfall sehr großer Lastwiderstände?
Die größte Abweichung vom linearen Verlauf tritt, wie sich durch die Diagramme der 3
Widerstände zeigt, tritt für jeweils in etwa bei einem r1 = 0,8 auf.
Seite 43
Anfängerpraktikum 1 - PW1
Allacher & Krieger
4. Formeln
Arithmetischer Mittelwert
x=
1 N
!x
N i=1 i
Mittlere quadratische Abweichung
1 N
! =
(x i " x ) 2
#
N " 1 i=1
2
Standardabweichung
1 N
(x i " x ) 2
#
N " 1 i=1
!=
Standardabweichung des Mittelwertes
!m =
!
N
Fehlerverteilung von Gauß
(x $x 0 )
1
$
2" 2 dx
e
" 2#
2
! (x)dx =
$%
& ! (x)dx = 1
+%
Absoluter Fehler
! a = E rwartet " M essung
Relativer Fehler
!r =
"m
•100%
x
Relative Häufigkeit
gi =
H
hi
Gewichtung auf unterschiedliche Maßklassen
Seite 44
Anfängerpraktikum 1 - PW1
Allacher & Krieger
l=
1 N
l h + l h + .... + lk hk
li = 1 1 2 2
!
N i=1
h1 + h2 + ... + hk
! k2 =
1 N
# (l " l )2
N " 1 i=1 i
Gewichtung bei verschiedenen Messmethoden
g1 : g2 : ...: g j =
1
1
1
:
: ....:
! m1 ! m 2
! mj
k
xg =
"x g
j
j =1
k
"g
j =1
j
j
k
! gm =
" (x
j =1
j
# x g )2 g j
k
(k # 1) " g j
j =1
Gauß’sche Fehlerfortpflanzung
2
2
2
k
# "f &
# "f &
# "f &
! = % ( ! 12 + .... + % ( ! k2 = ) % ( ! i2
$ "x1 '
$ "x k '
i=1 $ "x i '
2
y
Relativer Fehler eines Produktes nach Gauß’schem Fehlerfortpflanzung
2
" !1 %
"! k %
"! y %
$ ' = $ ' + ... + $ '
# y&
# x1 &
# xk &
2
2
Lineare Funktion:
y = ax + b
n
n
# n
&
N = n % ! x i2 " ! x i ! x i (
$ i=1
'
i=1
i=1
a=
n
n
,
1) n
(n
x
y
)
"
x
yi .
!
!
!
i i
i
+
N * i=1
i=1
i=1
-
b=
n
n
,
1)n 2 n
x
y
"
x
!
!
i ! i
i ! xi yi .
+
N * i=1 i=1
i=1
i=1
-
Seite 45
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Standardabweichung der Einzelmessungen um den Messpunkt
v i = y i ! (ax i + b)
n
#v
" y2 =
2
i
i=1
n!2
Standardabweichung für den Anstieg und Achsenabschnitt
!a = !y
n
N
k
!b = !y
"x
2
i
i=1
N
Dichte
m
V
!=
Schwingungsdauer
T = 2!
l
g
Erdbeschleunigung
4! 2 l
g= 2
T
Ohm’sche Gesetz
I=
U
R
Leistung im Gleichstromnetzwerk
P = IU
Kirchhoff’sche Maschenregel
!U + ! I R
k
k
k
=0
k
Kirchhoff’sche Knotenregel
!I
k
=0
k
Seite 46
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Spannungsteiler
U1 U 2
=
R1 R2
UR1
U1 =
(R1 + R2 )
Belasteter Spannungsteiler
I=
U ! UL UL UL
=
+
R ! R1
R1 RL
Spannungsverhältnis
UL
r1rL
=
U rL + r1 (1! r1 )
Serienschaltung von Widerständen
Rg = ! Ri
i=1
Parallelschaltung von Widerständen
1
1
=!
Rg
k Rk
Kapazitiver Widerstand (Farad) im Wechselstromkreis
!i
"C
1
Zc =
"C
Zc =
Induktiver Widerstand (Henry) im Wechselstromkreis
Z L = j!L
Z L = !L
Serienschaltung von R und C im Wechselstromkreis
Z = R!
2
j
"C
Z = R2 +
1
("C) 2
Serienschaltung von R und L im Wechselstromkreis
Seite 47
Anfängerpraktikum 1 - PW1
Allacher & Krieger
Z = R ! j"L
Z = R 2 ! ("L) 2
2
Klemmspannung
U K = U 0 ! IRi
Seite 48