Vorbereitung für 4. Klassenarbeit – Dreiecke

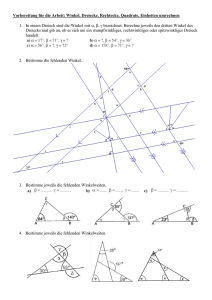
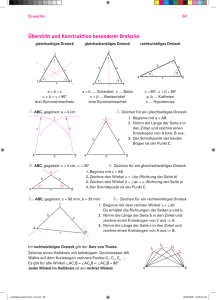
Vorbereitung für die Arbeit: Winkel, Dreiecke, Rechtecke, Quadrate, Einheiten umrechnen
1. In einem Dreieck sind die Winkel mit , , bezeichnet. Berechne jeweils den dritten Winkel des
Dreiecks und gib an, ob es sich um ein stumpfwinkliges, rechtwinkliges oder spitzwinkliges Dreieck
handelt.
2. Bestimme die fehlenden Winkel.
3. Bestimme jeweils die fehlenden Winkelweiten.
4. Bestimme jeweils die fehlenden Winkelweiten.
5. Bestimme folgende Winkel.
6. Benenne die Dreiecke nach Winkeln und nach Seiten.
allgemein
gleichschenklig
gleichseitig
spitzwinklig
13; 17
2; 7; 8; 11; 15; 16; 20
4; 9: 14
rechtwinklig
6; 12; 18
1
stumpfwinklig
5; 10; 19
3
7. Zeichne ein Dreieck mit den folgenden Eigenschaften.
a. Rechtwinklig und gleichschenklig
b. stumpfwinklig und allgemein
8. Wahr oder falsch? Begründe.
a. Ein stumpfwinkliges Dreieck hat zwei spitze Winkel.
Wahr, weil wenn man den stumpfen Winkel (>90˚) von 180˚ abzieht bleibt nur genug übrigh um
zwie stumpfe winkel zu formen.
b. Wenn ein Dreieck allgemein ist, so ist es spitzwinklig.
Falsch, allgemein bedeutet alle 3 Seiten haben verschiedene Längen. Das beeinflusst aber nicht
die Winkel.
c. Wenn ein Dreieck gleichschenklig ist, so ist es stumpfwinklig.
Falsch, da der Winkel zwischen den Schenkeln auch stumpf oder recht sein kann.
d. Wenn ein Dreieck gleichschenklig ist, so ist es auch gleichseitig.
Falsch, es kann gleichseitig sein, muss es aber nicht.
e. Wenn ein Dreieck rechtwinklig ist, so ist es nicht stumpfwinklig.
Wahr, das ein rechter Winkel 90˚ ist und nur 90˚ für die anderen 2 Winkel übrig bleibt.
9. Zeichne folgende Dreiecke im Koordinatensystem. Bestimme die Dreiecksformen nach Seiten und
Winkel.
a. A(-2|-3); B(2|-3); C(1|1)
b. A(-1|4); B(-1|-2); C(5|-2)
Spitzwinklig, allgemein
c. A(-3|4); B(0|2); C(5|5)
Stumpfwinklig, allgemein
10. Konstruiere die folgenden Dreiecke.
rechtwinklig, gleichschenklig
11. Zeichne eine Strecke
die 8 cm lang ist. Konstruiere die Mittelsenkrechte durch den Mittelpunkt
M.
12. Zeichne einen Winkel α = 50˚. Konstruiere die
Winkelhalbierende dieses Winkels.
13. Zeichne das Dreieck mit den Ecken A(6/5), B(1/1) und C(2/7) und konstruiere den Umkreis.
14. Zeichne das Dreieck mit den Ecken A(7/5), B(1/1)
und C(3/6) und konstruiere den Inkreis.
15. Zeichne das Dreieck mit den Ecken A(6/3), B(1/1)
und C(3/7) und zeichne alle Seitenhalbierenden ein.
Bestimme den Schwerpunkt des Dreiecks.
16. Zeichne das Dreieck mit den Ecken A(6/7),
B(1/2) und C(7/1) und zeichne alle Höhen ein.
Bestimme den Höhenschnittpunkt.
17. Berechne die Flächeninhalte der Dreiecke. Berechne den
Umfang des Dreiecks in Teil d.
18. Zeichne eine Skizze und berechne den Flächeninhalt und den Umfang des Rechtecks mit den Seiten
a = 19,5 m und b = 12 m.
19. Zeichne eine Skizze und berechne den Flächeninhalt und den Umfang des Quadrates mit der
Seitenlänge a = 4,7 m.
20. Herr Meier will die Giebelseite seines Hauses mit Platten
verkleiden. Wie groß ist die zu verkleidende Fläche, wenn die
beiden Fenster jewils eine Länge von 2,2 m und eine Höhe von 1,2
m haben?
21. Berechne die Flächeninhalte der aus Rechtecken und rechtwinkligen Dreiecken zusammengesetzten
Figuren. (Maße in m.)
a.
b.
c.