tutor08

Institut für Informatik
Lehrstuhl für Informatik 15
Computer Graphik & Visualisierung
Diskrete Strukturen I
Wintersemester 2006/2007
Tutorübung 8
Seite 1 von 3
Prof. R. Westermann, J. Schneider, J. Georgii, S. Pott
TU München, 11.12.2006
Tutorübung zu Diskrete Strukturen I (Blatt 8)
Aufgabe A [* Punkte] Satz von Cayley
Spannbäume:
Im Folgenden möchten wir uns mit der Frage beschäftigen, wieviele verschiedene Spannbäume ein
beliebiger Graph G hat. Dazu stellen wir am Beispiel des K3 fest, dass man sich entscheiden muss,
ob man isomorphe Spannbäume, die aber unterschiedliche Knotennamen haben unterscheidet oder
nicht. Wir beschränken uns der Einfachheit halber hier auf das Zählen von markierten Bäumen, wir
unterscheiden also isomorphe Bäume durch ihre Knotenmarkierungen.
Prüfercode:
Desweiteren führen wir als kompakte Schreibweise für Bäume den Prüfercode (Heinz Prüfer) ein. Der
Prüfercode eines Baumes T = (V, E) mit |V | = n ist die Zeichenkette der Länge n − 2, die folgender
Algorithmus konstruiert:
Eingabe: Baum T = (V, E)
Ausgabe: Wort t1 t2 . . . tn−2 über dem Alphabet {1, . . . , n}
i := 1
while |V | > 2 do
Bestimme Blatt v mit kleinster Markierung
ti := Nachbar von v im Baum T
Entferne v aus V und die entsprechende inzidente Kante {v, ti } aus E
i := i+1
end
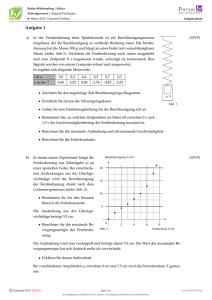
1
5
3
4
6
2
7
Abbildung 1. Beispielbaum.
a) Generieren Sie den Prüfercode für den obigen Baum.
b) Argumentieren Sie, warum der obige Algorithmus korrekt funktioniert und wieso der Prüfercode
zu einem gegebenen Spannbaum mit gegebenen Knotenindices eindeutig bestimmt ist.
Satz von Cayley:
Für n ≥ 2 Knoten gibt es genau nn−2 markierte Bäume.
c) Finden Sie einen Algorithmus, der aus einem Prüfercode wieder den Baum rekonstruiert.
d) Beweisen Sie den Satz von Cayley!
Hinweis: Zeigen Sie dazu, dass es eine Bijektion zwischen der Menge der Püfercodes und der Menge
aller markierten Spannbäume gibt. Zählen Sie dann die Menge aller Prüfercodes zu |V | = n.
Seite 2 von 3
Lösungen:
Aufgabe A [* Punkte] Satz von Cayley
Prüfercode:
a) Der zugehörige Prüfercode ist 33446.
b) Zunächst zeigen wir folgende Lemmata:
Lemma 1:
Jeder Baum T = (V, E) mit |V | ≥ 2 hat mindestens zwei Blätter.
Beweis
T enthält nach Definition keine Kreis. Also starten wir mit einer beliebigen Kante und konstruieren einen Pfad, indem wir an beiden Knoten der ursprünglichen Kante weitere Kanten
einfügen, “bis es nicht mehr weitergeht”, d.h. bis wir einen Startpunkt a und einen Endpunkt b
mit deg( a) = deg(b) = 1 gefunden haben. a, b sind offensichtlich Blätter.
Lemma 2
Ist T = (V, E) ein Baum und a ein Blatt, dann ist auch T ′ := T [V \{ a}] (knoteninduzierter Teilgraph) ein Baum.
Beweis
T ′ ist kreisfrei, da T kreisfrei war, und keine neuen Kanten hinzugefügt wurden. T ′ ist auch
zusammenhängend, da T zusammenhängend war. Da deg( a) = 1 hat a also folglich nur einen
Nachbarn c in T. c muss aber noch “am Baum T ′ hängen”, denn zu jedem Knoten x in T gab es
ja auch einen Pfad zu c.
Prüfercode: Nach Lemma 1 und 2 gibt es also in jedem Schritt des Algorithmus mindestens 2
Blätter, und in jedem Schritt ist der Restgraph noch ein Baum. Da der Algorithmus immer nur
das Blatt mit kleinster Markierung entfernt, und die Markierungen paarweise verschieden sind,
ist die Konstruktion des Prüfercodes zu gegebenem Spannbaum eindeutig. Da der Algorithmus
in jedem Schritt genau ein Blatt entfernt oder terminiert, muss er nach endlicher Zeit terminieren. Die Länge n − 2 ergibt sich aus der Beobachtung, dass jedes entfernte Blatt bis auf die letzten
zwei (Terminierung bei |V | = 2) genau eine Ziffer des Codes generiert.
Satz von Cayley:
c) Mit b) ist die Abbildung der Menge der Spannbäume auf die Menge der Prüfercodes eine (totale)
Funktion. Im Folgenden zeigen wir die Injektivität dieser Abbildung, indem wir eine eindeutige Umkehrabbildung von Prüfercodes auf Bäume konstruieren. Die Surjektivität folgt dann aus
der Tatsache, dass die Umkehrabbildung wiederum eine totale Funktion ist. Zeige also: Zu jedem Prüfercode gibt es einen eindeutigen Spannbaum. Beweis: Wiederum durch Konstruktion.
Eingabe: Prüfercode, also Wort t1 t2 t3 . . . tn−2 über dem Alphabet [n]
Ausgabe: Baum T = ([n], E)
S := ⊘
for i from 1 to n-2 do
Wähle kleinsten Knoten si ∈ [n]\ S, der nicht in ti . . . tn−2 vorkommt
Füge die Kante ei := {si , ti } in den Graphen ein
S := S ∪ {si }
end
Füge die Kante en−1 := [n]\ S in den Graphen ein
Seite 3 von 3
d) Betrachte den obigen Algorithmus. Für n = 2 wird die for-Schleife nie durchlaufen. In der
letzten Zeile des Algorithmus wird folglich korrekterweise {1, 2} als einzige Kante in den Baum
eingefügt. Für n > 2: Im Prüfercode kommen gerade die Blätter des Baumes nicht vor1 , daher
muss die kleinste nicht im Prüfercode vorkommende Zahl gleichzeitig das kleinste Blatt des
Baumes sein. Das rechtfertigt die Wahl von s1 und der Kante {s1 , t1 }. In der Konstruktion des
Prüfercodes wurde das kleinste Blatt nach Festlegung von t1 gestrichen. Im Algorithmus wird
dies dadurch realisiert, dass s1 in die Menge S aufgenommen wird und somit im nächsten Schritt
für die Wahl des kleinsten Blattes des Baums mit Prüfercode t2 . . . tn−2 nicht mehr in Betracht
gezogen wird.
Als Folgerung aus der Bijektion zwischen Prüfercodes und markierten Spannbäumen folgt nun sofort
dass die Menge aller Prüfercodes und die Menge aller Spannbäume zu einem Graphen mit n Knoten die gleiche Mächtigkeit haben. Somit gibt es nn−2 Prüfercodes und auch ebenso viele markierte
Spannbäume.
1
Genauer: Es kommt jeder Knoten v genau deg( v) − 1-mal vor.