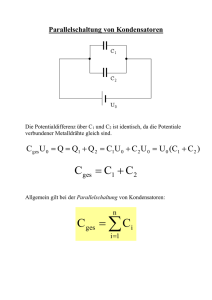
Parallelschaltung von Kondensatoren

Parallelschaltung von Kondensatoren
Einleitung:
Bei einer Parallelschaltung von Kondensatoren ist die Gesamtkapazität gleich der Summe der
Einzelkapazitäten. Cges = C, + C2 + C3 …
Die Teilströme verhalten sich proportional zu der jeweiligen Kapazität, ihre Summe ergibt den
Gesamtstrom IC ges. Die Spannung UC ist bei einer Parallelschaltung von
allen Kondensatoren gleich.
Versuch:
Es ist durch Strom- und Spannungsmessungen und unter Zugrundelegung der Annahme, dass der
Blindwiderstand eines Kondensators Xc = 1/wC ist, nach zuweisen, dass bei einer Parallelschaltung
von Kondensatoren die Gesamtkapazität gleich der Summe der Einzelkapazitäten ist.
Versuchsablauf:
Versuch nach Schaltung aufbauen und Funktionsgenerator anschließen und folgende Spannung
einstellen:
Ueff = 3 V (Sinus);
•
•
•
•
f = 1 kHz
Gesamtstrom Icges und Teilströme Ic1, Ic 2, Ic3 mit einem Multimeter messen und Werte in
Tabelle eintragen.
Blindwiderstände XC ges, XC1, X C2, X C3 mit der Formel XC = Uc/ IC berechnen.
Einzelkapazitäten und Gesamtkapazität mit der Formel C = 1 / w * Xc ermitteln.
Im Versuch ermittelte Gesamtkapazität Cges rechnerisch überprüfen.
Schaltung:
Tabelle:
Teil- und Gesamtstrom [mA]
Messpunkte
A-B (ICges )
C-D(IC1) E-I (I C2) G-H (I C ges)
35,415
4,705
10,07
20,64
Kondensatorspannung [V]
Messpunkte
D-I (UC 1)
F-I (UC 2)
H-I (UC 3)
3,17
3,17
3,17
Berechnung der Blindwiderstände:
X C1 =
X C3 =
U C1
I C1
UC3
IC3
=
3 ,17 V
= 673 , 75 Ω
4 , 705 mA
=
3 ,17 V
= 153 , 6 Ω
20 , 64 mA
X C2 =
X Cges =
UC2
IC2
UC
ges
I Cges
=
3 ,17 V
= 314 ,8 Ω
10 , 07 mA
=
3 ,17 V
= 89 , 5 Ω
35 , 41 mA
Berechnung der Kapazitäten:
C1 =
1
1
=
= 0 , 236 µ F
2π ⋅ f ⋅ X C
2 π ⋅ 1000 Hz ⋅ 673 , 75 Ω
C2 =
1
1
=
= 0 , 505 µ F
2π ⋅ f ⋅ X C 2
2 π ⋅ 1000 Hz ⋅ 314 ,8 Ω
C3 =
1
1
=
= 1 µF
2π ⋅ f ⋅ X C 3
2 π ⋅ 1000 Hz ⋅ 153 , 6 Ω
C ges =
1
1
=
= 1, 77 µ F
2 π ⋅ f ⋅ X Cges
2 π ⋅ 1000 Hz ⋅ 89 ,5 Ω
Rechnerische Überprüfung der Gesamtkapazität:
Cges = C1 + C2 + C3 = 0,236µF + 0,505µF + 1µF = 1,77µF
Erfolgstest Kondensator
1. Durch welches Bauteil wird beim Anlegen der Speisespannung der Strom begrenzt ?
Der Strom wird durch den Vorwiderstand Rv begrenzt .
2. Laden Sie den Kondensator auf . Beschreiben Sie die Zeigerbewegung des Amperemeters beim
Laden ?
Die Zeigerbewegung vollzieht sich zuerst schnell und wird danach langsamer .
3. Überbrücken Sie während eines Ladevorganges den Widerstand kurzzeitig . Der Kondensator ist
dann aufgeladen . Beschreiben Sie die Bewegung des Zeigers nach der Umschaltung in die
Entladestellung?
Der Zeiger des Messgerätes geht gleichmäßig gegen Null.
4. Wie verhalten sich Lade- und Entladestrom zueinander ?
Der Ladestrom erreicht schlagartig seinen Maximalwert . Der Entladestrom sinkt allmählich
ähnlich wie eine e-Funktion .
5. In welcher Schalterstellung wird der Kondensator geladen bzw. entladen ?
Schalterstellung 1 entspricht dem Ladevorgang .
Schalterstellung 2 entspricht dem Entladevorgang .
6. Beschreiben Sie die Bewegung des Instrumentenzeigers an der Kondensatorspannung in
Richtung auf den Wert der Speisespannung beim Laden des Kondensators ?
Beim Laden des Kondensators bewegt sich der Zeiger des Messinstrumentes gleichmäßig .
7. Schließen Sie den Widerstand kurzzeitig durch Überbrücken . Der Kondensator ist nun voll
geladen . Heben Sie den Kurzschluß auf und schalten Sie auf die Entladestellung des Schalters .
Beschreiben Sie die Zeigerbewegung während des Entladevorganges ?
Beim Entladen des Kondensators bewegt sich der Zeiger des Messinstrumentes gleichmäßig .
8.Wie ist die Polarität der Spannung am Kondensator beim Laden und Entladen ?
Die Polarität des Kondensator ist gleich der Polarität der Ladespannung .