Versuchsprotokoll 4. RC-Schaltungen - fk-wind

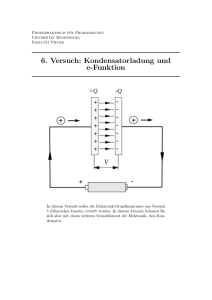
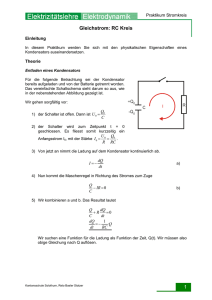
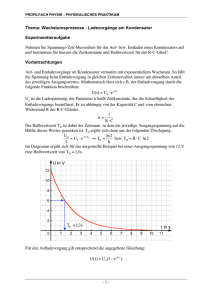
Laborversuch Elektrotechnik I
Versuch 4: RC-Schaltungen
Hochschule Bremerhaven
Prof. Dr. Oliver Zielinski / Hans Stross
Versuchsprotokoll
Datum:
Teilnehmer:
Name:
1.
2.
3.
4.
Testat
Matrikelnummer:
4. RC-Schaltungen
Für die elektronische Signalverarbeitung sind Schaltungen aus Widerständen (R) und
Kondensatoren (C) sehr wichtig. Die Schaltungen bilden so genannte dynamische
Systeme. Ein dynamisches System stellt eine Funktionseinheit dar zur Verarbeitung
und Übertragung von Signalen, wobei die Systemeingangsgrößen als Ursache und
die Systemausgangsgrößen als deren zeitliche Auswirkung zueinander in Relation
gebracht werden. Eingangs- und Ausgangssignal können nun - im Gegensatz zu
einem Widerstandsnetzwerk - unterschiedliche Verläufe aufweisen.
4.1 RC-Schaltung 1
Die Grundschaltung (Abbildung 4.1) besteht aus der Reihenschaltung von
Widerstand R und Kondensator C. Das Verhalten der Ausgangsspannung u2=uC und
des Stromes i=iC bei Laden und Entladen des Kondensators wird dabei durch
Exponentialfunktion beschrieben, die in Abbildung 4.2 dargestellt sind und in der
Vorlesung hergeleitet wurden.
Abbildung 4.1: RC-Schaltung 1
ETT1 – Labor, Versuch 4: RC-Schaltungen
Seite 1
Abbildung 4.2: Laden und Entladen in der RC-Schaltung 1
Das Produkt RC wird als Zeitkonstante T bezeichnet und hat die Dimension einer
Zeit. So ergibt sich z.B. für einen Widerstand von R=10kO und einen Kondensator
von C=1µF eine Zeitkonstante von T=0.01s.
Die Zeitkonstante lässt sich auch aus dem Bild ablesen, wenn man den Schnittpunkt
der Anfangssteigung mit dem Endwert der Spannung bestimmt. Die zugehörige Zeit
ist die Zeitkonstante T.
ETT1 – Labor, Versuch 4: RC-Schaltungen
Seite 2
4.2 RC-Schaltung 2
In dieser Schaltung sind R und C vertauscht (Abbildung 4.3). Als Resultat ist die
Schaltung für eine Gleichspannung undurchlässig (der Kondensator wirkt nach dem
anfänglichen Aufladen als Lücke) und wird z.B. auch für die Entfernung von
Gleichsignalen aus Messwerten verwendet.
Abbildung 4.3: RC-Schaltung 2
Da sich nur die Reihenfolge der Bauelement, nicht aber die Schaltung, geändert hat,
lässt sich die Spannung u2=uR für eine sprungförmige Spannung u1 zu:
u 2 = u1 − uC = u1 − u1 (1 − e
−1
T
) = u1e
−1
T
berechnen, d.h. einem exponentiellen Abfall, wobei sich die Zeitkonstante T wieder
aus dem Schnittpunkt der (negativen) Anfangssteigung mit dem Endwert der
Spannung (hier 0V) bestimmen lässt.
ETT1 – Labor, Versuch 4: RC-Schaltungen
Seite 3
4.3 Aufgaben
Ø Skizzieren Sie Eingangs- und Ausgangsspannung folgender Schaltung für eine
vorgegeben Einstellung des Potentiometers. Als Eingangsspannung u1
verwenden Sie eine Rechteckspannung aus dem Funktionsgenerator. Die
Frequenz ist dabei so zu wählen, dass die Einschwingvorgänge abgeschlossen
sind.
Bild 4.4: RC-Schaltung 1 im Versuchsaufbau.
Eingangsspannung:_____________ Frequenz:
Widerstand (Poti) R:
________________________
_____________________________________________
Wert des Kondensators C:
________________________________________
Ø Bestimmen Sie die Zeitkonstante grafisch.
T= ________________________
Ø Vergleichen Sie die Zeitkonstante mit dem rechnerischen Wert. T=RC=_______
Volts/div=______________ Time/div=___________________
ETT1 – Labor, Versuch 4: RC-Schaltungen
Seite 4
Ø Verwenden Sie nun die nachfolgende Schaltung und eine andere Einstellung des
Potentiometers.
Bild 4.5: RC-Schaltung 2 im Versuchsaufbau.
Eingangsspannung:_____________ Frequenz:
Widerstand (Poti) R:
________________________
_____________________________________________
Wert des Kondensators C:
________________________________________
Ø Bestimmen Sie die Zeitkonstante grafisch.
T= ________________________
Ø Vergleichen Sie die Zeitkonstante mit dem rechnerischen Wert. T=RC=_______
Volts/div=______________ Time/div=___________________
ETT1 – Labor, Versuch 4: RC-Schaltungen
Seite 5