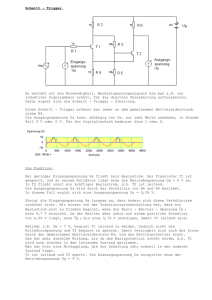
∫ ∫ ∫

Ergänzungen zu Versuch 2.7
Einfache RC-Schaltungen
RC-Glied als Integrator
Die Spannung ua(t) am Ausgang eines RC-Glieds (siehe Figur) entspricht unter bestimmten Bedingungen
dem Integral der Spannung ue(t) am Eingang.
ue(t)
C
ua(t)
Im folgenden wird die Funktionsweise der Schaltung erläutert und die Bedingung unter welcher sie arbeitet
hergeleitet.
Unter der Annahme, dass ua « ue ist, kann für die Stromstärke in R und C geschrieben werden
i(t ) =
u e (t ) − u a (t ) u e (t )
≈
R
R
Für den Kondensator gilt ferner i(t ) = C
und somit du a (t ) ≈
du a (t )
du (t ) u (t )
, damit gilt C a ≈ e ,
dt
dt
R
1
u e (t ) dt .
RC
u a (t)
Integrieren dieses Ausdrucks liefert:
∫ dua ≈
u a ( 0)
1
RC
t
∫ ue ( τ) dτ, bzw. ua (t ) = ua (0) +
0
1
RC
t
∫ u ( τ) dτ
e
0
Die Ausgangsspannung der Schaltung entspricht dem Integral der Eingangsspannung. Die obere
Integrationsgrenze des bestimmten Integrals entspricht der laufenden Zeit.
Um die Bedingung herzuleiten, unter welcher die oben hergeleitete Formel gilt, wird der Einfachheit halber
angenommen, dass die Eingangspannung sinusförmig verläuft. Bei sinusförmigem Verlauf der
Eingangspannung wird auch die Ausgangsspannung sinusförmig verlaufen.
ˆ sin(ω t ) liefert u (t ) ≈ R C du a (t ) = R CU
ˆ ω cos(ω t ) = U
ˆ cos(ω t ) . Der Vergleich
Der Ansatz u a (t ) = U
a
e
a
e
dt
ˆ ≈U
ˆ .
der Amplituden liefert die Beziehung: R C ω U
a
e
Die Annahme ua(t) « ue(t) ist dann erfüllt, wenn für die Amplituden Ûa « Ûe gilt. Dazu muss R Cω » 1,
1
1
T
bzw. R C » =
=
sein.
ω 2π f 2π
Das RC-Glied verhält sich also als Integrator, wenn die Zeitkonstante der Schaltung τ = R C viel grösser ist
als die Periodendauer T = 1/f des Eingangssignals:
τ»T
Das Verhältnis zwischen τ und T ab dem die Schaltung ihre Funktion erfüllt ist nicht eindeutig. Es muss je
nach Signalform empirisch ermittelt werden.
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
19. Juni 2004, © M. Schlup
2/6
Ergänzungen zu Versuch 2.7
RC-Glied als Integrator, Zeitkonstante τ = 1 s
1
0.5
0
-0.5
-1
4.4
4.5
4.6
4.7
Zeit in s
4.8
4.9
5
4.4
4.5
4.6
4.7
Zeit in s
4.8
4.9
5
0.05
0
-0.05
Figur Simulation: "Integriertes" Rechtecksignal bei einem Verhältnis τ/T = 1 s/0.2 s = 5. Die Flanken des
Dreiecksignals sind in Wirklichkeit Exponentialfunktionen.
RC-Glied als Integrator, Zeitkonstante τ = 1 s
1
0.5
0
-0.5
-1
4.4
4.5
4.6
4.7
Zeit in s
4.8
4.9
5
4.4
4.5
4.6
4.7
Zeit in s
4.8
4.9
5
0.02
0
-0.02
Figur Simulation: "Integriertes" Sinussignal bei einem Verhältnis τ/T = 1 s/0.2 s = 5. Man beachte, dass
bei der Integration das Ausgangssignal um eine Viertel-Periode verzögert wird.
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
19. Juni 2004, © M. Schlup
Ergänzungen zu Versuch 2.7
3/6
CR-Glied als Differentiator
Die Spannung ua(t) am Ausgang eines RC-Glieds (siehe Figur) entspricht unter bestimmten Bedingungen
der zeitlichen Ableitung der Spannung ue(t) am Eingang.
ue(t)
ua(t)
Im folgenden wird die Funktionsweise der Schaltung erläutert und die Bedingung unter welcher sie arbeitet
hergeleitet.
Für die Stromstärke in R und C kann geschrieben werden:
i(t ) = C
 du (t ) du (t ) 
d(u e (t ) − u a (t ))
du c
=C
= C e − a 
dt
dt
dt 
 dt
 du (t ) du (t ) 
du a (t ) u a (t ) du e (t )
Damit ergibt sich u a (t ) = R i(t ) = R C  e − a  , umgeformt:
+
=
dt 
dt
RC
dt
 dt
Unter der Bedingung
du e (t )
du a u a
«
gilt näherungsweise u a (t ) ≈ R C
dt
dt R C
Die Ausgangsspannung der Schaltung entspricht somit der zeitlichen Ableitung der Eingangsspannung.
Um die Bedingung herzuleiten, unter welcher die oben hergeleitete Formel gilt, wird der Einfachheit halber
angenommen, dass die Eingangspannung sinusförmig verläuft. Bei sinusförmigem Verlauf der
Eingangspannung wird auch die Ausgangsspannung sinusförmig verlaufen.
du a (t )
ˆ cos(ω t ) und somit gilt für die Bedingung
= ωU
a
dt
ˆ
ˆ « U a . Das heisst R C « 1 , bzw. mit ω = 2 π f = 2 π ergibt sich R C « T .
ωU
a
RC
ω
T
2π
Der Ansatz
ˆ sin(ω t )
u a (t ) = U
a
liefert
Das RC-Glied verhält sich also als Differentiator, wenn die Zeitkonstante der Schaltung τ = R C viel kleiner
ist als die Periodendauer T = 1/f des Eingangssignals:
τ«T
Das Verhältnis zwischen T und τ ab dem die Schaltung ihre Funktion erfüllt ist nicht eindeutig. Es muss je
nach Signalform empirisch ermittelt werden.
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
19. Juni 2004, © M. Schlup
4/6
Ergänzungen zu Versuch 2.7
CR-Glied als Differentiator, Zeitkonstante τ = 0.01 ms
2
1
0
-1
-2
2.5
3
3.5
4
4.5
5
4
4.5
5
Zeit in ms
0.1
0
-0.1
2.5
3
3.5
Zeit in ms
Figur Simulation: "Differenziertes" Sinussignal bei einem Verhältnis T/τ = 1 ms/0.01 ms = 100. Man
beachte, dass bei der Differentiation das Ausgangssignal um eine Viertel-Periode vorläuft.
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
19. Juni 2004, © M. Schlup
Ergänzungen zu Versuch 2.7
5/6
DC-Entkopplung
Der Kondensator soll allfällige Gleichspannungskomponenten der Eingangsspannung "abklemmen". Am
Ausgang der Schaltung sollten nur "Wechselanteile" der Eingangsspannung erscheinen.
ue(t)
ua(t)
Im folgenden wird die Funktionsweise der Schaltung erläutert und die Bedingung unter welcher sie arbeitet
hergeleitet.
du a (t ) u a (t ) du e (t )
Analog zum Abschnitt CR-Glied als Differentiator ergibt sich die Beziehung:
+
=
dt
RC
dt
du a (t ) du e (t )
du a u a
≈
Unter der Bedingung
»
gilt näherungsweise
dt
dt
dt R C
Diese Beziehung bedeutet für den Zusammenhang zwischen Eingangs- und Ausgangsspannung
(Überprüfung durch Bilden der Ableitung): u e (t ) ≈ U 0 + u a (t ) . Beide Spannungen unterscheiden sich nur
durch einen konstanten Term. Würde nun die Eingangsspannung nur aus einer Gleichspannung bestehen,
so würde sich der Kondensator auf diese aufladen und es würde kein Signal am Ausgang der Schaltung
erscheinen. Besteht nun die Eingangsspannung aus einer Gleich- und einer Wechselspannung, so wird
gemäss dem Superpositionsprinzip (die Schaltung ist linear!) nur der Wechselanteil am Ausgang
erscheinen, da sich ja der Kondensator unabhängig vom Wechselanteil auf den Gleichspannungsanteil
auflädt.
Um die Bedingung herzuleiten, unter welcher die oben hergeleitete Formel gilt, wird der Einfachheit halber
angenommen, dass der Wechselanteil der Eingangspannung sinusförmig verläuft. So wird auch die
Ausgangsspannung sinusförmig verlaufen.
ˆ
ˆ sin(ω t ) liefert du a (t ) = ω U
ˆ cos(ω t ) und die Bedingung wird zu ω U
ˆ » Ua .
Der Ansatz u a (t ) = U
a
a
a
RC
dt
1
1
T
=
bzw. R C » =
ω 2π f 2π
Das RC-Glied koppelt also DC-Anteile aus, wenn die Zeitkonstante der Schaltung τ = R C viel grösser ist
als die Periodendauer T = 1/f des Wechselanteils des Eingangssignals:
τ»T
Das Verhältnis zwischen τ und T ab dem die Schaltung ihre Funktion erfüllt ist nicht eindeutig. Es muss je
nach Signalform empirisch ermittelt werden.
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
19. Juni 2004, © M. Schlup
6/6
Ergänzungen zu Versuch 2.7
CR-Glied als DC-entkopplung, Zeitkonstante τ = 0.1 ms
3
2
1
0
-1
0.44
0.45
0.46
0.47
Zeit in ms
0.48
0.49
0.5
0.44
0.45
0.46
0.47
Zeit in ms
0.48
0.49
0.5
2
1
0
-1
-2
Figur Simulation: DC-Entkopplung für ein Rechtecksignal bei einem Verhältnis τ/T = 100 µs/10 µs = 10.
CR-Glied als DC-entkopplung, Zeitkonstante τ = 0.1 ms
3
2
1
0
-1
0.44
0.45
0.46
0.47
Zeit in ms
0.48
0.49
0.5
0.44
0.45
0.46
0.47
Zeit in ms
0.48
0.49
0.5
2
1
0
-1
-2
Figur Simulation: DC-Entkopplung für ein Sinussignal bei einem Verhältnis τ/T = 100 µs/10 µs = 10.
——————————————————————————————————————————————————
Zürcher Hochschule Winterthur, Departement T
19. Juni 2004, © M. Schlup