Sind von den Grössen a1, an, n, d, sn 3 Grössen gegeben, so

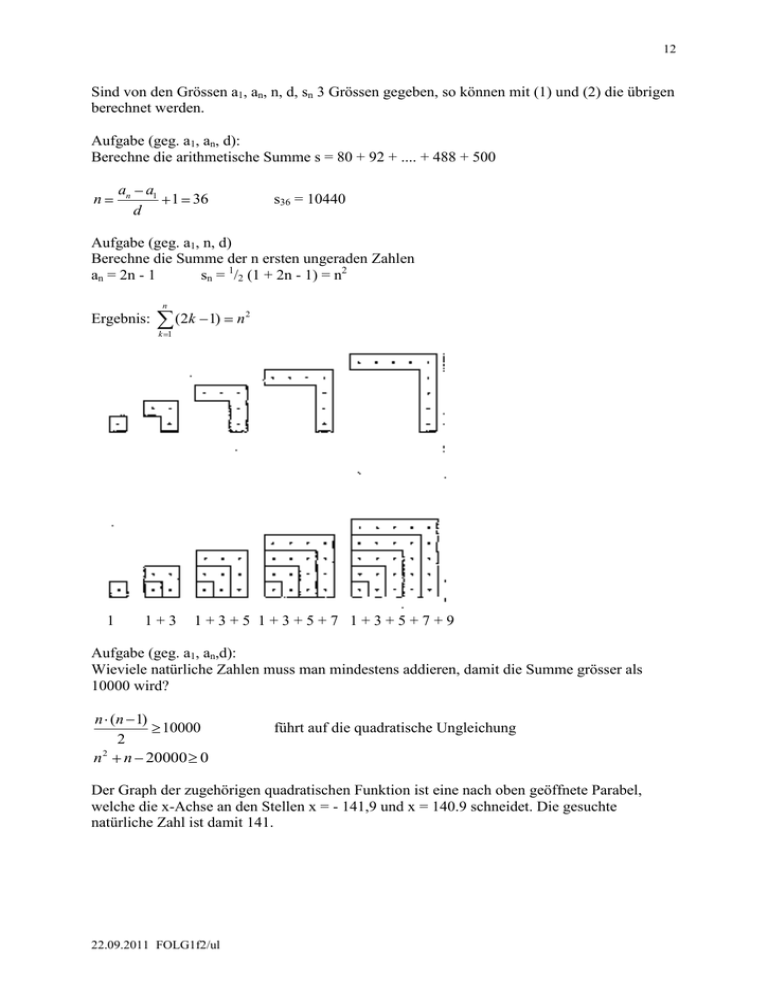
12
Sind von den Grössen a1, an, n, d, sn 3 Grössen gegeben, so können mit (1) und (2) die übrigen
berechnet werden.
Aufgabe (geg. a1, an, d):
Berechne die arithmetische Summe s = 80 + 92 + .... + 488 + 500
an a1
1 36
d
n
s36 = 10440
Aufgabe (geg. a1, n, d)
Berechne die Summe der n ersten ungeraden Zahlen
an = 2n - 1
sn = 1/2 (1 + 2n - 1) = n2
n
Ergebnis:
(2k 1)
n2
k 1
1
1+3
1+3+5 1+3+5+7 1+3+5+7+9
Aufgabe (geg. a1, an,d):
Wieviele natürliche Zahlen muss man mindestens addieren, damit die Summe grösser als
10000 wird?
n (n 1)
10000
2
n 2 n 20000 0
führt auf die quadratische Ungleichung
Der Graph der zugehörigen quadratischen Funktion ist eine nach oben geöffnete Parabel,
welche die x-Achse an den Stellen x = - 141,9 und x = 140.9 schneidet. Die gesuchte
natürliche Zahl ist damit 141.
22.09.2011 FOLG1f2/ul
13
Aufgabe:
In einer AF mit 21 Gliedern beträgt die Summe aller Glieder mit Ausschluss des ersten 710,
mit Ausschluss des letzten hingegen 650. Berechne das erste, das letzte Glied und die
Differenz d.
a21 = a1 + 20d
(1)
s21 – a1 = 710
s21 = a1 + 710
(2)
s21 – a21 = 650
s21 = a21 + 650 = a1 + 20d + 650
(3)
Gleichsetzen der rechten Seiten von (2) und (3) führt auf
a1 + 20d + 650 = a1 + 710 bzw. d = 3
Die Summe s21 kann nun wegen (2) auf zwei Arten dargestellt werden:
a a
2a 20d
2a 60
s21 21 1 21 21 1
21 1
21 (a1 30)
2
2
2
s21 = a1 + 710
Gleichsetzen der rechten Seiten ergibt 21 a1 +21 30 = a1 + 710 und schliesslich
a1 = 4 und mit (1) a21 = 64
Aufgabe (geg. a1, sn, d)::
Theater von Epidauros: In einem Theater hat die erste Reihe 40 Plätze, in jeder folgenden
Reihe gibt es 12 Plätze mehr. Insgesamt hat das Theater 7232 Plätze. Wieviele Reihen hat das
Theater?
a1 = 40
sn = 7232
sn = ½ n(a1 + a1 + (n - 1)d)
Das Theater von Epidauros
22.09.2011 FOLG1f2/ul
d = 12
3n2 + 17n - 3616 = 0
n1 = 32, n2 < 0