Analytische Geometrie

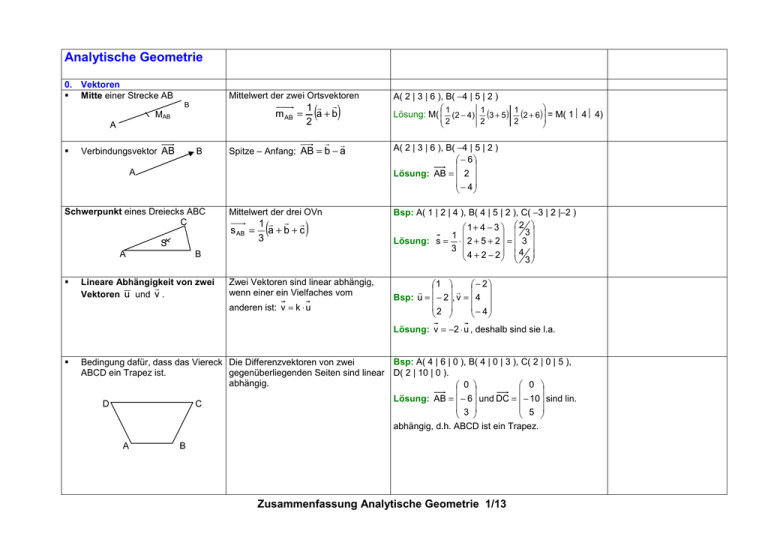
Analytische Geometrie
0. Vektoren
Mitte einer Strecke AB
m AB
MAB
A
Mittelwert der zwei Ortsvektoren
B
Verbindungsvektor AB
B
1 = a+b
2
(
)
S
A
2

1
(3 + 5 ) 1 (2 + 6 ) = M( 1 4 4)
2
2

A( 2 | 3 | 6 ), B( −4 | 5 | 2 )
 − 6


Lösung: AB =  2 
 − 4


Mittelwert der drei OVn
Bsp: A( 1 | 2 | 4 ), B( 4 | 5 | 2 ), C( −3 | 2 |−2 )
 1 + 4 − 3   2 3 

1 
Lösung: s = ⋅  2 + 5 + 2  =  3 
3 
 4 
 4 + 2 − 2   3 
s AB
1 = a+b+c
3
(
)
B
Lineare Abhängigkeit von zwei
Vektoren u und v .
1
Lösung: M(  (2 − 4)
Spitze – Anfang: AB = b − a
A
Schwerpunkt eines Dreiecks ABC
C
A( 2 | 3 | 6 ), B( −4 | 5 | 2 )
Zwei Vektoren sind linear abhängig,
wenn einer ein Vielfaches vom
anderen ist: v = k ⋅ u
1 
− 2

  
Bsp: u =  − 2 , v =  4 
2 
 − 4
 


Lösung: v = −2 ⋅ u , deshalb sind sie l.a.
Bsp: A( 4 | 6 | 0 ), B( 4 | 0 | 3 ), C( 2 | 0 | 5 ),
Bedingung dafür, dass das Viereck Die Differenzvektoren von zwei
gegenüberliegenden Seiten sind linear D( 2 | 10 | 0 ).
ABCD ein Trapez ist.
abhängig.
 0 
 0 




Lösung: AB =  − 6  und DC =  − 10  sind lin.
D
C
 3 
 5 




abhängig, d.h. ABCD ist ein Trapez.
A
B
Zusammenfassung Analytische Geometrie 1/13
1. Geraden
Gerade h durch den Punkt A in
Richtung u
X
A
u
x
a
O
Spurpunkt der Geraden g:
x = a + tu, t ∈ IR mit der x1x2Ebene.
Spurpunkt der Geraden g:
x = a + tu, t ∈ IR mit der x2x3Ebene.
Der OV x eines beliebigen
Geradenpunktes X ist die Summe aus
a und einem Vielfachen des RVs u .
1 
 
Bsp: Punkte A( 2 | 3 | 1 ), Richtung u =  2 
 − 1
 
2
 1
 
 
Lösung: g: x =  3  + t ⋅  2  , t ∈ R
 1
 − 1
 
 
.
x1 = a1 + tu1
 2
4
 
 
Im LGS * x2 = a2 + tu2 x3 = 0 setzen,
Bsp: g: x =  3  + λ − 1, λ ∈ IR
x3 = a3 + tu3
 1
 1
Gleichung lösen und Lösung in andere
 
 
Gleichungen von (*) einsetzen
Lösung: 1 + λ = 0 ergibt S1 ( -2  5  0 )
Im LGS (*) x1 = 0 setzen
 2
4 
 
 
Bsp: g: x =  3  + λ − 1, λ ∈ IR
1 
1 
 
 
Lösung:
Spurpunkt der Geraden g:
x = a + tu, t ∈ IR mit der x1x3Ebene.
Im LGS (*) x2 = 0 setzen
 2
2 
 
 
Bsp: g: x =  3  + λ − 1, λ ∈ IR
1 
1 
 
 
Lösung:
Liegt der Punkt P auf der Geraden
g: x = a + tu, t ∈ IR ?
(Punktprobe)
In der Geradengleichung statt x den
OV p des Punktes P einsetzen und
entstandenes LGS lösen.
Wenn sich kein Widerspruch ergibt,
folgt P ∈ g.
S2 ( 0  3,5  0,5 )
S3 ( 8  0  4 )
 2
2 
 
 
Bsp: P(−2 | 5 |−1), g: x =  3  + λ − 1, λ ∈ IR
1 
1 
 
 
Lösung: -2 = 2 + 2λ
5=3 − λ
-1 = 1 + λ
λ = −2, d.h. P ∈ g.
Zusammenfassung Analytische Geometrie 2/13
Gerade h durch P und parallel
zu g: x = a + tu, t ∈ IR
OV p als Stützvektor von h und RV u
von g ebenfalls als RV von h wählen:
h: x = p + t ⋅ u, t ∈ IR
g
P
h
Gerade h durch P und
orthogonal zur Ebene E: nx = d
h
E
P
Gerade g: x = a + tu, t ∈ IR als
Punkt geschrieben
Die Punkte Pt liegen auf einer
Geraden.
2. Lage von zwei Geraden
Lage von zwei Geraden
g: x = a + tu, t ∈ IR und
h: x = b + sv, s ∈ IR zueinander
OV p als Stützvektor von h und
Normalenvektor n von E als RV von h
wählen
h: x = p + λ ⋅ n, λ ∈ IR
Pt (a1 + tu1  a2 + tu2  a3 + tu3 )
 2
2 
 
 
Bsp: P(−2 | 5 |−1), g: x =  3  + λ ⋅  − 1, λ ∈ IR
1 
1 
 
 
 − 2
2 
 
 
Lösung: h: x =  5  + t ⋅  − 1, λ ∈ IR
− 1 
1 
 
 
Bsp: E1: 2 x1 + 3 x2 – 4 x3 = 12, P(−2 | 5 |−1)
Lösung:
 − 2
2 




h: x =  5  + λ ⋅  3 , λ ∈ IR
−1
 − 4




Die 3 Zeilen der Parametergleichung
nebeneinander als Koordinaten
schreiben
 2
2 
 
 
Bsp: g: x =  3  + λ ⋅  − 1, λ ∈ IR
1 
1 
 
 
Lösung: Pt( 2+2t | 3 −t | 1+t )
Pt ( a1 + tu1..a2 + tu2  a3 + tu3 )
Bsp: Pt( 4 - t | 2 + 2t | −t )
Die Koordinaten als die 3 Zeilen der
Parametergleichung schreiben und
in Vektorschreibweise aufspalten
Lösung: g: x =  2  + t ⋅  2 , t ∈ IR
1. Schritt: u, v linear abhängig?
Ja. Parallel oder identisch.
Nein. 2. Schritt: Gleichsetzen
a1 + tu1 = b1 + sv1
LGS
a2 + tu2 = b2 + sv2 lösen.
a3 + tu3 = b3 + sv3
Es gibt Lösung → SchnittP
Keine Lösung → windschief
Achtung:
LGS mit 3 Gleichungen und 2 Var. !
z.B. Teil-LGS lösen und Probe in 3 Gl.
 4
 
 −1 
 
0
 
 − 1
 
Bsp:
 2
2 
1 
0
 
 
 
 
g: x =  3  + λ − 1 ; h: x =  − 2  + µ1 
1 
1 
1 
3
 
 
 
 
Lösung:
u, v linear unabhängig, also g und h nicht parallel.
2+2λ = 1
3 - λ = -2+µ
hat keine Lösung. Damit haben
1 + λ = 1+3µ
g und h keinen Schnittpunkt, d.h. g, h windschief.
Zusammenfassung Analytische Geometrie 3/13
Mittelparallele s der parallelen
Geraden g und h
A
g
s
h
B
3. Ebenen
Parametergleichung der Ebene
u
v
E
p
O
Koordinatengleichung der
n
Ebene
E
Parametergleichung →
Koordinatengleichung
OV des Mittelpunkts M der Strecke AB
 2
2 
4 
2 
 
 
 
 
als Stützvektor und RV von g bzw. h
g: x =  3  + λ − 1 , h: x =  − 1 + λ − 1
als RV wählen.
1 
1 
3 
1 
 
 
 
 
Für g: x = a + tu, t ∈ IR und
3
2
 
 
s:
=
−
+
µ
Lösung:
x
1
 
 − 1
h: x = b + sv, s ∈ IR ist dann die Mittel2
 1
1
 
 
a + b + ru , r ∈ R
parallele s: x =
2
( )
Der Ortsvektor x eines beliebigen
Ebenenpunkts X ist die Summe aus
dem Ortsvektor p eines
Ebenenpunktes P und passenden
Vielfachen der Spannvektoren
u und v .
E: a x1 + b x2 + c x2 = d
a
 
Normalenvektor: n =  b 
c 
 
siehe GTR - Spalte
Spurpunkte der Ebene
E: ax1 + bx2 + cx3 = d
sind die Schnittpunkte von E mit
den Koordinatenachsen
2 x1 – 2 x2 – x3 = 9
Normalenform der Ebene nx = d
Parametergleichung dreizeilig
schreiben und dann die Parameter
eliminieren
oder
E: x = p + λ ⋅ u + µ ⋅ v, λ, µ ∈ IR
2 


 − 2 x = 9
−1


1 
 2
1 
 
 
 
E: x =  2  + λ1  + µ 0 , λ ∈ IR
3
1 
 2
 
 
 
Lösung: -2x1 + 3x2 + x3 = 7
Achsenabschnittsform herstellen durch E: 2x1 + 3x2 – 4x3 = 12
Division der Koordinatengleichung
durch d.
Lösung: Division durch 12 liefert
Die Koordinaten der Spurpunkte
x1 x 2 x 3
+
= 1 und damit die Spurpunkte
+
lassen sich an den entstandenen
6
4
−3
Nennern ablesen.
S1(600), S2(040), S3(00-3).
Zusammenfassung Analytische Geometrie 4/13
Drei beliebige, nicht
kollineare Punkte der
Ebene bestimmen und in
ax1 + bx2 + cx3 = 1
einsetzen, LGS lösen.
Dann möglichst
ganzzahlige Koeffizienten
a,b,c herstellen durch
Multiplikation der
entstandenen Gleichung.
4. Aufstellen von
Ebenengleichungen
Ebene E durch die drei Punkte A,
B und C
B
A
C
Zum Beispiel den Ortsvektor von P als
Stützvektor und den Richtungsvektor
Q+
von g und den Vektor QP als
Spannvektoren wählen.
+P
Ebene E, die die beiden Geraden
g und h enthält
A
h
g
Ebene E, die die beiden parallelen
Geraden g und h enthält
Q
h
g
P
Voraussetzung ist hier, dass die
Geraden sich schneiden
Zum Beispiel den Stützvektor von g
als Stützvektor von E und die
Richtungsvektoren von g und h als
Spannvektoren wählen
E
AB und AC als Richtungsvektoren
wählen
Voraussetzung ist hier, dass P nicht
auf der Geraden liegt.
Ebene E, die die Gerade g und
den Punkt P enthält
g
Zum Beispiel den Ortsvektor von A als
Stützvektor und die Vektoren
Zum Beispiel den Stützvektor p von g
als Stützvektor von E und als
Spannvektoren den Vektor PQ und
den Richtungsvektor von g wählen.
A( 3 | 2 | 0 ), B( 4 | 4 | 2 ) und C( 5 | 2 | -1 )
Lösung:
3
 1
2
 
 
 
E: x =  2  + r ⋅  2  + s ⋅  0  , r, s ∈ IR
0
 2
 − 1
 
 
 
1 
 2
 
 
g: x =  2  + λ1 , λ ∈ IR , P( 4 | 2 | 2 )
3
1 
 
 
Lösung:
 4
2
3
 
 
 
E: x =  2  + r ⋅  1  + s ⋅  0  , r, s ∈ IR
 2
 1
 − 1
 
 
 
1 
 2
1 
0 
 
 

 

Bsp: g: x =  2  + λ1  , h: x =  − 4  + µ1 
3
1 
0 
 − 2
 
 


 
Lösung:
1 
 2
 0 
 
 
 
E: x =  2  + λ1  + µ 1 , λ, µ ∈ IR
3
1 
 − 2
 
 
 
1 
2 
3
 − 2
 
 
 
 
Bsp: g: x =  2  + λ − 1 , h: x =  2  + µ1 
3
2 
1 
 − 2
 
 
 
 
Lösung:
1 
2 
 2 
 
 
 
E: x =  2  + λ − 1 + µ 0 , λ, µ ∈ IR
3
2 
 − 2
 
 
 
Zusammenfassung Analytische Geometrie 5/13
Ebene E, die die Gerade g enthält
und parallel zu h ist
h
Zum Beispiel den Stützvektor von g
als Stützvektor von E und die
Richtungsvektoren von g und h als
Spannvektoren wählen
1 
 2
1 
0 
 
 

 

Bsp: g: x =  2  + λ1  ; h: x =  − 4  + µ1 
3
1 
2 
 − 2
 
 

 

Lösung:
1 
 2
 0 
 
 
 
E: x =  2  + λ 1  + µ 1 , λ, µ ∈ IR
3
 1
 − 2
 
 
 
E hat den Richtungsvektor von g als
Normalenvektor und geht durch den
Punkt A.
1 
2 
 
 
Bsp: A( 3 | 2 | −5) , g: x =  2  + λ − 1, λ ∈ IR ,
3
2 
 
 
g
Ebene E durch A und orthogonal
zur Geraden g
g
E
+A
5. Lage von Gerade g und Ebene E
zueinander
Die Gerade g ist parallel zur
Ebene E

 3   2 
   

Lösung: E :  x −  2  ⋅  − 1 = 0
 − 5   2 

   

Der Normalenvektor von E und der
Richtungsvektor von g sind orthogonal.
g
1 
 2
 
 
Bsp: g: x =  2  + λ1  , E: x1+ 4x2 – 3x3 = 2
3
 2
 
 
 2  1 
   
Lösung:  1  ⋅  4  = 2⋅1 + 1⋅4+2⋅(-3) = 0
 2  − 3 
   
d.h. E und g sind parallel.
Symmetrieebene F der Punkte A
und B
A
F
B
F hat den Vektor AB als
Normalenvektor und geht durch den
Mittelpunkt der Strecke AB
Bsp: A( 3 | 2 | −5) , B( 5 | 4 | 1 )
Lösung:

 4   2 

  

F:  x −  3  ⋅  2  = 0 bzw. F: x1 + x2 +3x3 = 1
 − 2   6 


  

Zusammenfassung Analytische Geometrie 6/13
6. Lage von Ebenen zueinander
Parallelität zweier Ebenen
E1 und E2
E1 und E2 haben linear abhängige
Normalenvektoren
E1
Lösung:
Die Normalenvektoren sind das (-2)-fache
voneinander, die Absolutglieder das 6-fache, d.h. E1
und E2 sind parallel und verschieden.
E2
Orthogonalität zweier Ebenen E1 E1 und E2 haben orthogonale
und E2
Normalenvektoren
E2
7. Schnitt von Ebenen / Geraden
Schnittgerade zweier Ebenen E1
und E2
E1
E2
Schnittpunkt einer Geraden g
mit einer Ebene E
g
E
Bsp: E1: x1+2 x2 – 3 x3 = 2,
E2: 5 x1+2 x2 + 3 x3 = 11
 1  5
   
Lösung:  2  ⋅  2  = 0 , d.h. E1 ⊥ E2
− 3 3
   
E1
Bsp: E1: x1+2 x2 – 3 x3 = 2,
E2: -2x1 − 4 x2 + 6 x3 = 12
Aus beiden Ebenengleichungen eine
Bsp: E1: x1+2 x2 – 3 x3 = 2, (1)
Gleichung herstellen, die nur 2
E2: x1+3 x2 + x3 = −1 (2)
Variablen enthält.
Darin eine Variable durch den
Parameter λ ersetzen und die
x2 + 4x3 = −3 (3) = (2) − (1)
Lösung:
anderen Variablen ebenfalls durch λ
Für x3 = λ folgt x2 = −3 − 4λ und x1 = 8 + 11λ
ausdrücken.
Die entstandenen drei Gleichungen als
ergibt Schnittgerade
Vektorgleichung schreiben.
 8 
 11 




g: x =  − 3  + λ ⋅  − 4 
x1 = 8 + 11λ
 0 
 1 
x2 = -3 − 4λ




x3 = λ
Die drei „Zeilen“ der
Parametergleichung der Geraden in
die Koordinatengleichung der Ebene
einsetzen, entstandene Gleichung
nach dem Parameter auflösen. Dieser
in die Parametergleichung eingesetzt
liefert die Koordinaten des
Schnittpunkts.
 − 5
 − 8
 
 
Bsp: E: 2x1 + 3x2 = 9; g: x =  2  + t ⋅  1 
 4 
 − 1
 
 
Lösung:
2(−5−8t) + 3(2+t) = 9 ergibt t = −1 und den
Schnittpunkt S( 3  1 5 )
Zusammenfassung Analytische Geometrie 7/13
8. Skalarprodukt
Länge der Strecke AB
A
B
(b
Bsp: A( 3 | 1 | −5) , B( 5 | 4 | 1 )
Lösung:
AB = AB = b − a =
1
− a1
) + (b
2
2
− a2
) + (b
2
3
− a3
)
2
Bedingung dafür, dass das Viereck Die Diagonalen sind gleich lang,
ABCD ein Quadrat ist.
orthogonal und halbieren sich.
D
C
AB = AB = (5 − 3)2 + ( 4 − 1)2 + (1 − ( −5))2 = 49 = 7
Bsp: A( 1 | −2 | 1 ), B( 3 | −4 | 2 ),
C( 4 | −2 | 4 ) und D( 2 | 0| 3 ).
 3   − 1
   
Lösung: AC = 18 = BD , AC ⋅ BD =  0  ⋅  4  = 0
 3   − 1
   
5
A
und MAC=MBD= 
2
B
Gerade g steht auf dem Quadrat
ABCD senkrecht und geht durch
die Quadratmitte.
h
AC und BD orthogonal ist.
Gleichung der Gerden durch MAC mit
Richtungsvektor n aufstellen.
D
C
A
Vektor n bestimmen, der zu (z.B.)
B
Bedingung dafür, dass das Viereck Die Diagonalen schneiden sich
ABCD eine Raute ist.
rechtwinklig und halbieren sich:
D
A
AC ⋅ BD = 0 und MAC = MBD
C
B
−2
5 
2 
Bsp: A( 1 | −2 | 1 ), B( 3 | −4 | 2 ),
C( 4 | −2 | 4 ) und D( 2 | 0 | 3 ).
Lösung: 3n1 + 3n3 = 0 und –n1 + 4n2 − n3 = 0 bzw.
 1
 
n1 = −n3 , n2 = 0,25⋅(n1+n3) führt auf n =  0 
 − 1
 
 2,5 
 1
 
 
MAC( 2,5  −2  2,5 ); g: x =  − 2  + t ⋅  0 
 2,5 
 − 1
 
 
Bsp: A( 2 | 3 | 1 ), B( 5 | 7 | 1 ),
C( 5 | 11 | 4 ) und D( 2 | 7| 4 ).
Lösung:
3  − 3
   
AC ⋅ BD =  8  ⋅  0  = 0 , MAC = MBD =
3  3 
   
Zusammenfassung Analytische Geometrie 8/13
7

 7 5
2
2 

Gegeben: Gerade g und Punkte
A, B ∉ g.
Gesucht ist C ∈ g, so dass
∠ACB ein rechter Winkel ist
Allgemeiner Geradenpunkt Ct ∈ g
g
C
Bedingung: AC t ⋅ BC t = 0 ergibt
quadratische Gleichung.
Deren Lösungen in die Gleichung von
g eingesetzt liefern die Koordinaten
der Punkte C1 und C2.
B
A
Bsp:
 − 4
2 
 


A( -1 | 3 | 1 ), B( −2 | 6 | 4 ), g: x =  7  + t ⋅  − 1
0 
2 

 

Lösung: Ct ( -4+2t  7−t  2t )
 − 3 + 2t   − 2 + 2t 

 

ACt ⋅ BCt =  4 − t  ⋅  1 − t  = 9t 2 − 25 t + 14 = 0
 − 1 + 2t   − 4 + 2t 

 

mit Lösungen t1 =
7
und t2 = 2.
9
 22 22 14 
 und C2 ( 0  5  4 )
C1  −

 9 3 9 
9. Winkel
Winkel zwischen zwei Geraden
g: x = a + λ u, λ ∈ IR und
h: x = b + µ v, µ ∈ IR
Der Winkel ϕ zwischen den Geraden g
 2
2 
1 
0
 
 
 
 
und h ist gleich dem Winkel zwischen Bsp: g: x =  3  + λ − 1 , h: x =  − 2  + µ1 
den Richtungsvektoren.
1 
1 
1 
3
 
 
 
 
Da man stets den kleineren Winkel
Lösung:
bestimmen will, steht in der Formel im
Zähler der Betrag.
 2  0 
  
 − 11 
1  3 
uv
− 1+ 3
1
  
=
=
cos ϕ = =
u v
6 10
2 15
15
ϕ ≈ 75,0
Winkel zwischen zwei Ebenen E1 Der Winkel ϕ zwischen den Ebenen
und E2
E1 und E2 ist gleich dem Winkel
zwischen den Normalenvektoren der
Ebenen.
Da man stets den kleineren Winkel
bestimmen will, steht in der Formel im
Zähler der Betrag.
0
Bsp: E1: x1+2 x2 – 3 x3 = 2, E2: 2 x1+2 x2 + x3 = 7,
Lösung:
cos ϕ =
n1 ⋅ n 2
n1 ⋅ n 2
ϕ ≈ 74,5
=
 1  2 

 
 2  2 
 − 3  1 

 
14 9
=
2+4−3
0
Zusammenfassung Analytische Geometrie 9/13
3 14
=
1
14
Winkel zwischen einer Geraden
g und einer Ebene E
g
ϕ
E
Der Winkel ϕ zwischen der Geraden g
und der Ebene E errechnet sich aus
dem Winkel zwischen dem RV der
Geraden und dem NV der Ebene
0
durch cos (90 − ϕ) = sin ϕ.
Da man stets den kleineren Winkel
bestimmen will, steht in der Formel im
Zähler der Betrag.
1 
2 
 
 
Bsp: g: x =  2  + λ − 1, λ ∈ IR , E: x1+2 x2 – 3 x3 = 2
3
2 
 
 
Lösung:
sin ϕ =
10. Abstände
Abstand Punkt – Ebene
P
.
E
Abstand Punkt – Ebene mit
Lotfußpunkt
P
E
.
F
u⋅n
u⋅n
=
 2  1 
 

 − 1 2 
 2  − 3 
 

9 14
=
6
3 14
Mit Hessescher Normalenform
(HNF)
Betrag des NV der Ebene E
bestimmen
Koordinatengleichung von E in die
Form ..... = 0 bringen und durch den
Betrag des NV dividieren; man erhält
die „HNF“ von E.
Setzt man jetzt die Koordinaten von P
ein, ergibt sich betragsmäßig der
Abstand von P zu E.
HNF:
Mit Lotgerade
Bsp: E: x1+2 x2 – 2 x3 = 17,
Lotgerade aufstellen.
Lösung:
Bsp: E: x1+2 x2 – 3 x3 = 2,
=
2
0
14
; ϕ ≈ 32,3
P( −3 I 5 I 2 )
Lösung:
n = 1 + 4 + 9 = 14 ;
1
14
d(P;E) =
( x 1 + 2x 2 − 3 x 3 − 2) = 0
1
14
(− 3 + 2 ⋅ 5 − 3 ⋅ 2 − 2)
=
1
14
P( 1 I 2 I 3 )
1  1 
Lotgerade mit der Ebene E schneiden. Lotgerade: x =  2  + t 2 , t ∈ IR
Der Schnittpunkt ist der Lotfußpunkt F.
 3  − 2

  
Der Abstand ist gleich dem Betrag des Lotgerade mit E schneiden leifert den Lotfußpunkt F
Verbindungsvektors PF , also d = PF . (siehe Schnitt Ebene - Gerade): −1 + 9t = 17, also
t = 2 und damit F( 3 I 6 I -1 ).
3 − 1 
2 




d = PF =  6 − 2  =  4  = 4 + 16 + 16 = 6
 − 1− 3
 − 4




Zusammenfassung Analytische Geometrie 10/13
Abstand paralleler Ebenen
+P
E1
Beliebigen Punkt P der Ebene E1
bestimmen
Abstand von P zu E2 mit HNF
berechnen
Bsp: E1: 2 x1+2 x2 – x3 = 2,
Lösung:
P(1 I 0 I 0 ) ∈ E1;
HNF von E2 :
E2
d(P;E2) =
Abstand Punkt – Gerade
Für den allemeinen Geradenpunkt Qt
den Vektor PQ t berechnen
g
Qt
u
+P
Bedingung PQ t ⋅ u = 0 ( u ist der RV
von g ) ergibt Gleichung in t, diese
lösen
Lösung für t in Gleichung von g
eingesetzt ergibt die Koordinaten des
Lotfußpunkt Q.
Die Entfernung PQ ist der gesuchte
Abstand.
E2: 2 x1+2 x2 − x3 = 7
1
( 2x 1 + 2x 2 − x 3 − 7 ) = 0
3
1
(1 + 2 ⋅ 0 − 0 − 7) = 7
3
3
2 
3 


 
Bsp: P( 3 I 2 I −1 ), g: x =  − 1 + t ⋅ 1 , t ∈ IR
 − 2
2 


 
Lösung:
 2t 


Qt( 3+2t I –1+t I 2–2t ) ∈ g; PQ t =  − 3 + t 
 3 − 2t 


 2t   2 
 


Bed. PQ t ⋅ u = 0 liefert  − 3 + t  ⋅ 1  = 0 bzw.
 3 − 2t   − 2 
 


4t – 3 + t – 6 + 4t = 0 ⇔ t = 1 und damit Q(5 I 0 I 0 )
 2 


PQ =  − 2  = 4 + 4 + 1 = 3
 1 


Abstand paralleler Geraden
P
g
h
Beliebigen Punkt P ∈ g bestimmen,
dessen Abstand von h berechnen
( siehe Abstand Punkt – Gerade )
3 
 
2 


2 
 
 − 2


2
 
2 


6
 
 − 2


Bsp: g: x =  − 1 + λ1  , h: x = 1  + λ1 
Lösung:
P( 3 I –1 I 2 ) ∈ g; Qt(2+2λ I 1+λ I 6-2λ ) ∈ h;
 2λ − 1   2 

 

Bed. PQ t ⋅ u = 0 liefert  λ + 2  ⋅  1  = 0 bzw.
 − 2λ + 4   − 2 

 

8
4λ − 2 + λ + 2 + 4λ − 8 = 0 ⇔ λ =
9
 7 
 1 2
1
1
1125 ≈ 3,7
7 + 262 + 202 =
PQ =  26  =
9
9
 9
−
20


Zusammenfassung Analytische Geometrie 11/13
Abstand windschiefer Geraden
Für die allgemeinen Geradenpunkte
g und h mit Fußpunkten P und Q Pr ∈ g und Qt ∈ h den Vektor
Pr Q t bestimmen
h
P
g
Q
Bedingungen Pr Q t ⋅ u = 0 und
Pr Q t ⋅ v = 0 ( u, v RVn von g bzw. h )
führen zu LGS, dieses lösen.
Die Lösungen in die Gleichungen von
g bzw. h eingesetzt ergeben die
Koordinaten der Lotfußpunkte
P und Q.
Pr Q t ⋅ v
=0
Abstand windschiefer Geraden
ohne Fußpunkte
g
A
H
h
Ebene H durch h parallel zu g legen,
Koordinatengleichung von H
berechnen
Beliebigen Punkt A ∈ g bestimmen.
Der Abstand von A zur Ebene H
( HNF ! ) ist der gesuchte Abstand der
windschiefen Geraden
 1
 
 1 


5
 
2
 
6
 
0
 
 6 + 2t − 2r 


ist Pr Q t =  1 − t + 2r  und die Bed.
 5−r 


führen zum LGS
bzw.
12+4t−4r–2+2t−4r+5−r = 0
12+4t−4r−1+t−2r
=0
5 + 2t − 3r = 0
11 + 5t − 6r = 0
mit der Lösung
r=1
t = -1
Lotfußpunkte P(1 I –2 I 2), Q(3 I 2 I 6)
PQ = PQ
 2 


Lösung:
Für Pr( -1+2r I –2r I 1+r) und Qt( 5+2t I 1-t I 6 )
PQ = PQ ist der gesuchte Abstand.
Pr Q t ⋅ u = 0
 − 1
 
Bsp: : g: x =  0  + r  − 2  ; h: x =  1  + t  − 1 .
=
(3 − 1)2 + (2 + 2)2 + (6 − 2)2
= 36 = 6
 − 1
 2 
5
2


 
 
 
Bsp: g: x =  0  + r  − 2  ; h: x =  1  + t  − 1 .
 1
 1 
6
0

 

 
 
Lösung: H : x1 + 2x2 + 2x3 − 19 = 0
HNF von H:
1
( x1 + 2x2 + 2x3 − 19 ) = 0
3
Für den Punkt A(-1 I 0 I 1) ∈ g ist dann
d(A;H) =
1
(− 1 + 2 ⋅ 0 + 2 ⋅ 1 − 19 ) = 6
3
Zusammenfassung Analytische Geometrie 12/13
Bestimmung von H
3 beliebige Punkte der
Ebene H wählen, z.B.
( 5 I 1 I 6 ), ( 7 I 0 I 6 ) und
( 7 I -1 I 7 ), diese in
ax1 + bx2 + cx3 = 1 (*)
einsetzen und LGS lösen.
(Im Menü EQUA SIML (F1),
dann F2 für 3 Unbekannte
wählen);
Lösungen in (*) einsetzen
und Gleichung mit 19
multiplizieren
Flächeninhalt eines
Parallelogramms PQRS
Abstand h des Punktes S von der
Geraden (PQ) bestimmen
Inhalt A = PQ ⋅ h
S
R
h
Bsp: P( 1 | 2 | 4 ), Q( 4 | 5 | 2 ),
R( −3 | 2 | −2 ) und S( −6 | −1| 0 ).
Lösung:
Ft( 1 + 3λ  3 + 3λ  4 − 2λ ) ∈ (PQ)
 7 + 3λ   3 
  

SFt ⋅ u =  3 + 3λ  ⋅  3  = 21 + 9λ + 9 + 9λ − 8 + 4λ = 0
 4 − 2λ   − 2 
  

ergibt λ = −1 und damit F(−2  −1  6 )
P
4
 
Q
h = SF =  0  = 52 = 2 13
6
 
Inhalt A = PQ ⋅ h =
Flächeninhalt eines Trapezes
PQTS.
S
T
Abstand h des Punktes S von der
Geraden (PQ) und
Länge m der Strecke M1M2 berechnen
Inhalt A = m⋅h
Bsp: P( 1 | 2 | 4 ), Q( 4 | 5 | 2 ),
T( −4,5 | 0,5 | −1 ) und S( −6 | −1 | 0 ).
Lösung: h = d(S;(PQ)) = 2 13
( siehe Flächeninhalt Parallelogramm )
M1(−2,5  0,5  2 ), M2 (−0,25  2,75  0,5 )
 2.25 


h
M1
P
m
M2
22 ⋅ 2 ⋅ 13 ≈ 33,8
m = M1M2 =  2,25  =
 − 1,5 


Q
A = m⋅h =
99 3 11
=
8
2 2
3 11
⋅ 2 13 ≈ 25,4
2 2
Zusammenfassung Analytische Geometrie 13/13