Weltraum Grössen im Weltraum

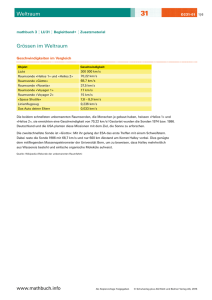
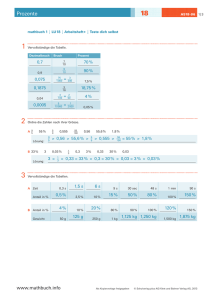
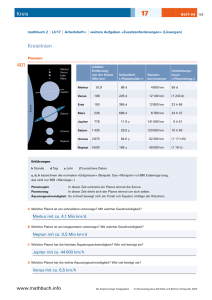
26
Weltraum
C226-01
mathbuch 3 LU 26 Begleitband Zusatzmaterial
Grössen im Weltraum
Geschwindigkeiten im Vergleich
Objekt
Geschwindigkeit
Licht
300 000 km / s
Raumsonde «Helios 1» und «Helios 2»
70,22 km / s
Raumsonde «Giotto»
68,7 km / s
Raumsonde «Rosetta»
37,5 km / s
Raumsonde «Voyager 1»
17 km / s
Raumsonde «Voyager 2»
15 km / s
«Space Shuttle»
7,8 – 8,0 km / s
Linienflugzeug
0,236 km / s
Das Auto deiner Eltern
0,033 km / s
Die beidem schnellsten unbemannten Raumsonden, die Menschen je gebaut haben, heissen «Helios 1» und
«Helios 2», sie erreichten eine Geschwindigkeit von 70,22 km / s! Gestartet wurden die Sonden 1974 bzw. 1986.
Deutschland und die USA planten diese Missionen mit dem Ziel, die Sonne zu erforschen.
Die zweitschnellste Sonde ist «Giotto»: Mit ihr gelang der ESA das erste Treffen mit einem Schweifstern.
Dabei raste die Sonde 1986 mit 68,7 km / s und nur 600 km Abstand am Komet Halley vorbei. Dies genügte
dem mitfliegenden Massenspektrometer der Universität Bern, um zu beweisen, dass Halley mehrheitlich
aus Wassereis besteht und einfache organische Moleküle aufweist.
Quelle: Wikipedia (Rekorde der unbemannten Raumfahrt)
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015
1 | 6
26
Weltraum
C226-01
mathbuch 3 LU 26 Begleitband Zusatzmaterial
Astronomische Entfernungseinheiten
Lichtgeschwindigkeit
Sie beträgt im Vakuum c = 299 792 458 m / s, das sind ca. 300 Millionen m / s.
Beispiele: Von der Sonne zur Erde braucht das Licht etwa 8 Minuten und 20 Sekunden,
vom Neptun zur Erde etwa 4 Stunden und vom Stern Proxima Centauri zur Erde etwa 4 Jahre und 3 Monate.
Im Weltraum kommt man mit der grössten Entfernungseinheit (km), die auf der Erde gilt, nicht mehr zurecht.
Darum werden für Berechnungen im Weltraum andere Einheiten verwendet:
Für Entfernungen im Sonnensystem: die Astronomische Einheit (AE)
Der mittlere Abstand zwischen Sonne und Erde wird Astronomische Einheit genannt und mit AE oder AU
(englisch: astronomical unit) abgekürzt. Die AE ist in der Astronomie ein wichtiges Entfernungsmass.
1 AE = 149 597 870 700 m, das sind ca. 150 Millionen km.
Für Entfernungen zu näheren Sternen: das Lichtjahr (Lj)
Zu den Sternen ist das Licht einige Jahre unterwegs. Um diese Distanzen beschreiben zu können,
wird die Masseinheit Lichtjahr Lj verwendet.
Ein Lichtjahr ist die Strecke, die das Licht im Vakuum innerhalb eines mittleren
Erdenjahres (365,26 Tage) durchläuft. Das sind knapp 10 Billionen Kilometer.
Für weitere Entfernungen: die Parallaxensekunde (Parsec, pc) mit Kiloparsec (kpc) und Megaparsec (Mpc)
1 Parsec entspricht 3,26 Lichtjahren.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015
2 | 6
26
Weltraum
C226-01
mathbuch 3 LU 26 Begleitband Zusatzmaterial
Die Leuchtkraft der Sterne
Am Himmel sehen wir stark und schwach leuchtende Sterne. Wie gross die Leuchtkraft eines Sterns
tatsächlich ist, lässt sich aus dieser Beobachtung nicht direkt sagen. Je stärker die Leuchtkraft ist,
desto heller erscheint uns der Stern. Je weiter ein Stern entfernt ist, desto weniger hell scheint er uns.
Von der Erde aus sieht man einen Stern mit seiner scheinbaren Helligkeit. Diese wird durch die Entfernung
und durch die interstellare Materie beeinflusst.
In der Astronomie interessiert auch die wirkliche Leuchtkraft. Die absolute Helligkeit der Himmelkörper
ist eine Hilfsgrösse in der Astronomie, um die tatsächlichen Helligkeiten, also die Leuchtkraft von Himmelsobjekten,
vergleichen zu können. Man geht von einer einheitlichen Entfernung aus und gibt dazu die entsprechende
Leuchtkraft an. Man vergleicht die Leuchtkraft der Sterne, wie wenn alle gleich weit entfernt wären.
Die einheitliche Entfernung wurde mit 10 Parsec (pc) festgelegt. Somit ist bei Sternen, die weniger als 10 pc
entfernt sind, die scheinbare Helligkeit grösser als die absolute Helligkeit.
Einheit für die Leuchtkraft der Sterne (mag)
Die Helligkeiten werden in der Einheit mag angegeben. Die lichtschwächsten Sterne haben eine Leuchtkraft
von +17 mag (etwa ein Zehntausendstel der Sonnenleuchtkraft). Die hellsten Fixsterne erreichen
absolute Helligkeiten von etwa − 9 mag. Das ist die über 100 000-fache Leuchtkraft der Sonne. Sie hat für
uns eine scheinbare Leuchtkraft von – 26 mag. Ihre absolute Leuchtkraft beträgt jedoch nur 4,83 mag.
Das bedeutet: Je kleiner die Zahl, desto heller leuchtet das Gestirn.
Quelle: Wikipedia (absolute Helligkeit)
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015
3 | 6
26
Weltraum
C226-01
mathbuch 3 LU 26 Begleitband Zusatzmaterial
Die hellsten Sterne am Nachthimmel 1
Sternname
scheinbare Helligkeit
absolute Helligkeit
Sternbild
Entfernung (Lj)
Sirius
– 1.46
1.43
Grosser Hund
8.6
Canopus
– 0.62
– 5.64
Kiel
312
Arcturus
– 0.05
– 0.31
Bootes
37
Alpha Centauri
– 0.01
4.4
Zentaur
4.4
0.03
0.58
Vega
Leier
25.3
Capella
0.08
– 0.49
Fuhrmann
Rigel
0.18
– 6.72
Orion
770
Kleiner Hund
11.4
Eridanus
145
Prokyon
0.4
2.64
Achernar
0.45
– 2.77
42
Beteigeuze
0.45
– 5.04
Orion
640
Hadar
0.61
– 5.42
Zentaur
525
Altair
0.76
2.21
Adler
16.7
Acrux
0.77
– 4.17
Kreuz
320
Aldebaran
0.87
– 0.64
Stier
65
Spica
0.98
– 3.56
Jungfrau
Antares
Pollux
Formalhaut
Becrux
Deneb
1.06
1.16
1.17
1.25
1.25
– 5.39
1.07
1.72
– 3.91
– 8.47
Skorpion
Zwillinge
Südliche Fische
Kreuz
Schwan
– 26.73
4.84
Sonne
262
604
33
25
352
3 200
1.488 · 10 – 6
1 Daten aus dem Programm «Stellarium»
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015
4 | 6
26
Weltraum
C226-01
mathbuch 3 LU 26 Begleitband Zusatzmaterial
Entfernung der Sterne bestimmen mithilfe des Daumensprungs
Das Phänomen des Daumensprungs (siehe AH 9 «Ähnlichkeit») kann zum Abschätzen von Entfernungen
genutzt werden.
Wir betrachten den aufgestellten Daumen des ausgestreckten Arms abwechselnd mit dem linken und
dem rechten Auge. Dabei scheint der Daumen vor dem weiter entfernten Hintergrund hin und her zu springen.
Grund dafür ist, dass wir den Daumen mit dem linken Auge aus einem etwas anderen Blickwinkel betrachten
als mit dem rechten Auge.
Wenn wir nun die Grösse eines entfernten Gegenstands wie zum Beispiel eines Hauses kennen, können wir
aufgrund der Länge des Daumensprungs auf die Entfernung dieses Gegenstands schliessen. Umgekehrt können
wir bei bekannter Entfernung auf die Grösse des Gegenstands schliessen. Das genaue Resultat hängt natürlich
von der individuellen Armlänge und des Augenabstandes ab. Nehmen wir für die Armlänge l = 70 cm und für den
Augenabstand b = 6 cm an. Dann folgt aus dem Strahlensatz für die Länge des Daumensprungs L D und die
gesuchte Entfernung D B:
b : l = LD : DB
LD
b
l
DB
Dasselbe Phänomen nutzen die Astronomen, um die Entfernung der Sterne zu bestimmen. Anstatt einen
Gegenstand einmal mit dem linken und dann mit dem rechten Auge zu betrachten, beobachten Astronomen
denselben Stern in den unterschiedlichen Jahreszeiten (z. B. Herbst – Frühling) durch ein Fernrohr und
messen die Abstände zu den benachbarten Sternen. Dabei stellen sie fest, dass nahe Sterne gegenüber
den weiter entfernten Sternen kleine Ellipsen am Himmel zu beschreiben scheinen.
Der Zusammenhang zwischen der Grösse der Bewegung und der Entfernung der Sterne lässt sich
folgendermassen erklären:
Im Verlauf eines Jahres kreist die Erde um die Sonne. Daher ändern wir ständig den Beobachtungsstandort
im Raum. Nahe Sterne scheinen sich folglich gegenüber den fernen Sternen zu verschieben, so wie
der Daumen vor dem weiter entfernten Hintergrund hin und her springt. Je näher der Stern, desto grösser
seine Verschiebung (der Daumen scheint umso weiter zu springen, je näher wir ihn ans Gesicht halten).
Sehr weit entfernte Sterne weisen eine so kleine scheinbare Bewegung auf, dass wir sie nicht mehr beobachten
können. Diese Hintergrundsterne zeigen also keine messbare parallaktische Verschiebung im Verlauf des Jahres.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015
5 | 6
26
Weltraum
C226-01
mathbuch 3 LU 26 Begleitband Zusatzmaterial
Die Erdbahn um die Sonne ist nahezu kreisförmig. Daher wird ein naher Stern, der sich bezüglich der Ebene
der Erdbahn (Ekliptik) genau senkrecht über der Sonne befindet, auch eine kreisförmige scheinbare Bewegung
relativ zu den Hintergrundsternen im Verlauf des Jahres vollziehen.
Stern (scheinbare Position)
scheinbare Bahn des Sterns (kreisförmig)
Stern (wahre Position)
Parallaxenwinkel
p
Sonne
Erde
Erdbahn (kreisförmig)
Die beobachtete Bewegung des nahen Sterns ist eine scheinbare Bewegung der an das Firmament
projizierten Position des Sterns aufgrund der Bewegung der Erde um die Sonne. Die wahre Position des Sterns
ändert sich ebenso wenig, wie der Daumen sich bewegt, wenn er einmal mit dem linken und einmal mit
dem rechten Auge betrachtet wird. Die Beobachtung mit dem linken bzw. dem rechten Auge entspricht dabei
den Beobachtungen an zwei Zeitpunkten im Jahr mit einem Unterschied von einem halben Jahr.
Also beispielsweise einer Beobachtung im Sommer und einer im Winter.
Die Grösse des Mondes überprüfen
Der aufgehende Vollmond erscheint uns manchmal gross und orange, manchmal ist er fast rötlich gefärbt.
Im Vergleich zum Mond, der hoch am Himmel steht, ist er deutlich grösser.
Der Mond verändert jedoch seine Grösse nicht. Überlege dir Experimente, wie du die Mondgrösse des
aufgehenden Mondes und des Mondes hoch am Nachthimmel messen und vergleichen kannst.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015
6 | 6