Kreis Kreislinien 401

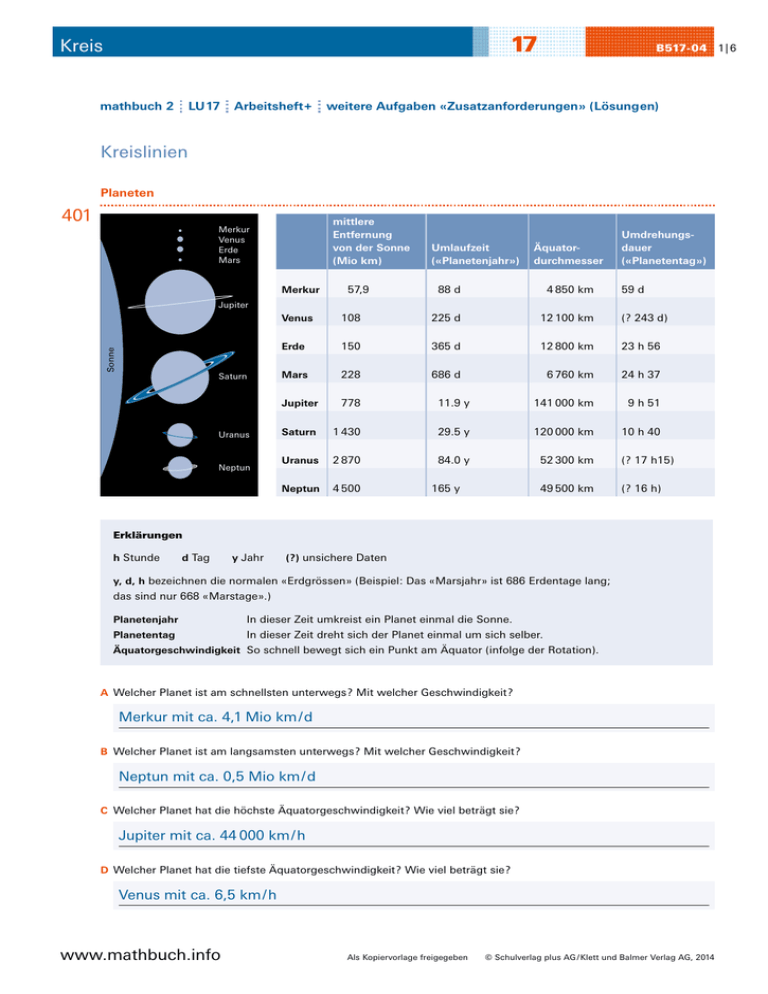
17
Kreis
B517-04
mathbuch 2 LU 17 Arbeitsheft+ weitere Aufgaben «Zusatzanforderungen» (Lösungen)
Kreislinien
Planeten
401
mittlere
Entfernung
von der Sonne
(Mio km)
Umlaufzeit
(«Planetenjahr»)
Äquatordurchmesser
Umdrehungsdauer
(«Planetentag»)
Merkur
   57,9
  88 d
  4 850 km
59 d
Venus
  108
225 d
  12 100 km
(? 243 d)
Erde
  150
365 d
  12 800 km
23 h 56
Mars
  228
686 d
  6 760 km
24 h 37
Jupiter
  778
  11.9 y
141 000 km
  9 h 51
Saturn
1 430
  29.5 y
120 000 km
10 h 40
Uranus
2 870
  84.0 y
  52 300 km
(? 17 h15)
Neptun
4 500
165 y
  49 500 km
(? 16 h)
Merkur
Venus
Erde
Mars
Sonne
Jupiter
Saturn
Uranus
Neptun
Erklärungen
h Stunde d Tag y Jahr (?) unsichere Daten
y, d, h bezeichnen die normalen «Erdgrössen» (Beispiel: Das «Marsjahr» ist 686 Erdentage lang;
das sind nur 668 «Marstage».)
Planetenjahr
In dieser Zeit umkreist ein Planet einmal die Sonne.
Planetentag
In dieser Zeit dreht sich der Planet einmal um sich selber.
Äquatorgeschwindigkeit So schnell bewegt sich ein Punkt am Äquator (infolge der Rotation).
A Welcher Planet ist am schnellsten unterwegs? Mit welcher Geschwindigkeit?
Merkur mit ca. 4,1 Mio km / d
B Welcher Planet ist am langsamsten unterwegs? Mit welcher Geschwindigkeit?
Neptun mit ca. 0,5 Mio km / d
C Welcher Planet hat die höchste Äquatorgeschwindigkeit? Wie viel beträgt sie?
Jupiter mit ca. 44 000 km / h
D Welcher Planet hat die tiefste Äquatorgeschwindigkeit? Wie viel beträgt sie?
Venus mit ca. 6,5 km / h
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2014
1 | 6
17
Kreis
B517-04
mathbuch 2 LU 17 Arbeitsheft+ weitere Aufgaben «Zusatzanforderungen» (Lösungen)
402
Die Planeten sind im Bild in Aufgabe 401 sind ungefähr massstäblich zur Sonne dargestellt.
A Bestimme aus der Darstellung die Grösse der Sonne.
Der Durchmesser des Sonnenkreises ist schätzungsweise 10-mal grösser ist als
der Durchmesser des Jupiterkreises. Der Äquatordurchmesser der Sonne beträgt
also etwa 1,4 Mio km.
B Der Mond umkreist die Erde in ca. 384 000 km Abstand. Hätte die Mondbahn in der Sonne Platz?
Ja, weil zweimal 384 000 km in 1,4 Mio. km Platz finden.
C Ein Äquatorpunkt auf der Sonnenoberfläche bewegt sich mit 7 180 km / h.
Wie lange dauert eine Äquatorumdrehung?
Ungefähr 600 Stunden, also etwa 25 Tage.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2014
2 | 6
17
Kreis
B517-04
mathbuch 2 LU 17 Arbeitsheft+ weitere Aufgaben «Zusatzanforderungen» (Lösungen)
Spitzbogenfenster
403
Gotisches Spitzbogenfenster
aus dem 13. Jahrhundert
A In einem grossen Kreis sind sechs identische kleinere Kreise so angeordnet,
dass sie sich und den grossen Kreis berühren. Der blaue Kreis im Zentrum berührt
die sechs kleineren Kreise. Ist er kleiner, grösser oder gleich gross wie diese?
Begründe deine Antwort.
Der mittlere Kreis ist genau gleich gross wie die anderen sechs Kreise.
Da die äusseren Kreise gleich gross sind, sind die Dreiecke gleichschenklig.
Die Winkel im Zentrum messen 60°. Also sind die Dreiecke gleichseitig.
Darum ist auch der innere Kreis gleich gross.
B In einem Halbkreis liegt ein Kreis.
Vergleiche die Länge des Halbkreisbogens mit dem Umfang des Kreises.
Der Halbkreisbogen ist genau gleich lang wie der Umfang des Kreises.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2014
3 | 6
17
Kreis
B517-04
mathbuch 2 LU 17 Arbeitsheft+ weitere Aufgaben «Zusatzanforderungen» (Lösungen)
C In einem 60°-Sektor liegt ein Kreis.
Vergleiche die Länge des Sektorbogens mit dem Umfang des Kreises.
Der Bogen ist halb so lang wie der Kreisumfang.
D In einem Halbkreis liegen zwei kleinere Halbkreise und ein Kreis. Die Figur ist 12 m breit.
Wie oft hat der Umfang des Kreises auf dem grossen Halbkreisbogen Platz?
Ergänze in der rechten Figur die Hilfslängen, die du zum Berechnen brauchst.
x
x
u
6–x
b
3
3
3 2 + (6 – x) 2 = (3 + x) 2 (Satz des Pythagoras)
Der Radius x des kleinen Kreises ist 2 m, der Umfang u misst 4 π.
Der Radius des grossen Halbkreises ist 6 m, der Bogen b misst 6 π.
Der Kreisumfang hat also 1,5-mal Platz auf dem Halbkreisbogen.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2014
4 | 6
17
Kreis
B517-04
mathbuch 2 LU 17 Arbeitsheft+ weitere Aufgaben «Zusatzanforderungen» (Lösungen)
E In einem Halbkreis liegen zwei Spitzbögen und ein kleiner Kreis. Die beiden Spitzbögen
sind über einem gleichseitigen Dreieck konstruiert. Die Figur ist 12 m breit.
Wie oft hat der Umfang des kleinen Kreises auf dem Halbkreisbogen Platz?
x
u
6–x
x
b
6
6
6 2 + (6 – x) 2 = (6 + x) 2 (Satz des Pythagoras)
Der Radius x des kleinen Kreises ist 1,5 m, der Umfang u misst 3 π.
Der Radius des grossen Halbkreises ist 6 m, der Bogen b misst 6 π.
Der Kreisumfang hat also 2-mal Platz auf dem Halbkreisbogen.
F In einem Spitzbogen liegen ein Halbkreis sowie ein kleiner Kreis.
Der Spitzbogen ist über einem gleichseitigen Dreieck konstruiert. Die Figur ist 12 m breit.
Wie oft hat der Kreisumfang auf dem Halbkreisbogen Platz?
Wie oft hat der Kreisumfang auf dem Spitzbogen Platz?
x
x
u
12
–
x
b
6
6
6 2 + (6 + x) 2 = (12 – x) 2 (Satz des Pythagoras)
Der Radius x des kleinen Kreises ist 2 m, der Umfang u misst 4 π.
Der Radius des grossen Halbkreises ist 6 m, der Bogen b misst 6 π.
Der Kreisumfang hat also 1,5-mal Platz auf dem Halbkreisbogen.
Der Radius des Spitzbogens ist 12 m, eine Seite l des Spitzbogens beträgt 4 π.
Der ganze Spitzbogen misst 8 π.
Der Kreisumfang hat also 2-mal Platz auf dem Spitzbogen.
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2014
5 | 6
17
Kreis
B517-04
mathbuch 2 LU 17 Arbeitsheft+ weitere Aufgaben «Zusatzanforderungen» (Lösungen)
Berechnungen am Kreis und Zylinder
404
Mit einem 10 m langen Gartenschlauch von 1,8 cm Innendurchmesser wird ein rundes Planschbecken
von 1,8 m Innendurchmesser gefüllt.
A Wie viele «Schlauchfüllungen» ergeben im Becken einen Pegelstand von 10 cm?
100
B Wie lange dauert es bei einer Schlauchleistung von 50 Liter pro Minute,
bis das Wasser im Becken 20 cm hoch steht?
10 Minuten
C Mit welcher Geschwindigkeit fliesst bei dieser Leistung das Wasser im Schlauch?
mit etwa 12 km / h (200 m / min)
405
Ein Zylinder ist 10 cm hoch und hat 4 cm Durchmesser. Zwei senkrecht übereinander liegende Punkte
auf dem oberen und dem unteren Rand werden mit einem gespannten Faden verbunden.
Der Faden läuft einmal um den Zylinder herum. Wie lang ist er?
etwa 16 cm
Um die Erde
406
Der Erdradius misst 6,37 · 10 3 km.
A Berechne die Geschwindigkeit eines Punktes am Erdäquator.
etwa 1 670 km / h
B Berechne die Flughöhe eines Satelliten, der die Erde mit 10 000 km / h in 24 h einmal umkreist.
etwa 30 000 km
www.mathbuch.info
Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2014
6 | 6