A519_01_Aufgaben

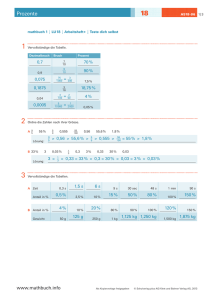
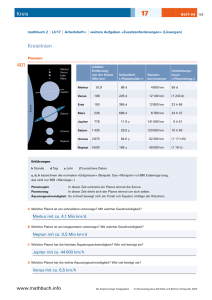
19
Summen und Produkte
mathbuch 1
301
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Rechne möglichst geschickt. Stelle den Rechnungsweg algebraisch dar.
Beispiel:
12 + 24 + 26 + 18 = (12 + 18) + (24 + 26) = 30 + 50 = 80
a + b + c + d = (a + d) + (b + c)
A
136 + 215 + 304 + 1 305 =
a+b+c+d =
B
237 + 226 + 203 + 2 304 =
a+b+c+d =
C
338 + 237 + 102 + 3 303 =
a+b+c+d =
D 101 + 205 + 101 + 205 + 188 =
a+b+a+b+c =
E
202 + 215 + 202 + 215 + 168 =
a+b+a+b+c =
F
303 + 225 + 303 + 225 + 148 =
a+b+a+b+c =
www.mathbuch.info
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
1 | 10
19
Summen und Produkte
mathbuch 1
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Modell-Eisenbahn
302
A Notiere einen Term für die Länge der Eisenbahnanlage und vereinfache ihn.
B Berechne die Länge der Eisenbahnanlage.
C Berechne die Fahrzeit für eine Runde auf der Anlage.
D Welche Geschwindigkeit hat der Zug ungefähr: 0,24 m / s oder 0,4 m / min?
Schienenstück
www.mathbuch.info
Als Kopiervorlage freigegeben
Länge
Fahrzeit
x = 41 cm
x = 1,7 s
y = 26 cm
y = 1,1 s
z = 39 cm
z = 1,6 s
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
2 | 10
19
Summen und Produkte
mathbuch 1
303
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
A Erstelle einen Term für die Länge der Eisenbahnanlage und vereinfache ihn.
B Berechne die Länge der Eisenbahnanlage.
C Berechne die Fahrzeit für eine Runde auf der Anlage.
Schienenstück
www.mathbuch.info
Als Kopiervorlage freigegeben
Länge
Fahrzeit
x = 41 cm
x = 1,7 s
y = 26 cm
y = 1,1 s
z = 39 cm
z = 1,6 s
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
3 | 10
19
Summen und Produkte
mathbuch 1
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Zugkompositionen berechnen
304
Ergänze die Tabellen anhand der Angaben im Katalog.
Lokomotive
(L)
Huckepackwagen
(H)
Staubgutwagen
(St)
Silowagen
(Si)
Schiebewandwagen
(Sch)
Länge [mm]
l 1 = 85,5
l 2 = 76
l 3 = 43
l 4 = 63
l 5 = 66
Preis [CHF]
p 1 = 295.50
p 2 = 51.60
p 3 = 42.00
p 4 = 40.60
p 5 = 42.50
Zug A:
L – H – Si – Si – Si – H
Der Zug besteht aus 1 Lokomotive, 2 Huckepackwagen
und 3 Silowagen.
als Term
Länge
1 · l1 + 2 · l2 + 3 · l4
Preis
1 · p1 + 2 · p2 + 3 · p4
Zug B:
L – St – St – Sch– Sch
als Term
in Zahlen
Total
1 · 85,5 + 2 · 76 + 3 · 63
mm
CHF
in Zahlen
Total
Länge
mm
Preis
CHF
Zug C:
als Term
Länge
in Zahlen
1 · l 1 + 2 · l 2 + 3 · l4
mm
Preis
www.mathbuch.info
Total
CHF
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
4 | 10
19
Summen und Produkte
mathbuch 1
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Zug D:
als Term
in Zahlen
Länge
Preis
305
Total
mm
2 · p1 + 1 · p2 + 3 · p3 + 2 · p5
CHF
Berechne die Zahl im Deckstein.
Wie musst du die untersten beiden Mittenzahlen verändern,
damit im Deckstein die Zahl 4 005 herauskommt?
Probiere aus, bis du eine Lösung gefunden hast.
420
442
www.mathbuch.info
443
420
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
5 | 10
19
Summen und Produkte
mathbuch 1
306
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Ergänze.
A
a+b
2c
2d
a+b
B
5x + 5y + 6z
x+y
307
x+y
Ergänze.
a+2
5
a+5
a
a+6
a
3
10
a + 2b
b
5
3
a + 4b + 10
10
www.mathbuch.info
a + 3b
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
6 | 10
19
Summen und Produkte
mathbuch 1
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Term-Mauern
308
In jedem Stein steht die Summe der beiden darunter liegenden. Fülle die Leerstellen.
a + 3b
a–b
3a + b
2(x + y)
(y + y)
3(x + y)
a+6
a
309
a+5
1
Vereinfache die Terme.
A
3(q + w + k) + 3w – 2q
=
B
q + 3(3w + k) + 4q =
C
3w + 10q + 4(k + m + 2) – (7m + q)
=
D 5m + 4(3k + m) + 5(3p + k) – 2k – 4m
www.mathbuch.info
=
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
7 | 10
19
Summen und Produkte
mathbuch 1
310
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Produkte berechnen und zerlegen
Ergänze die Rechendreiecke.
24
600
32
∙
25
6
∙
7
12
∙
15
25
36
175
24
35
∙
21
∙
12
12
∙
18
16
180
∙
28
25
22
720
∙
15
24
32
∙
48
25
600
www.mathbuch.info
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
8 | 10
19
Summen und Produkte
mathbuch 1
311
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Ergänze die Rechendreiecke.
A
8
144
192
144
∙
324
∙
12
144
∙
9
324
B
16
880
480
180
132
∙
∙
∙
660
1 050
165
15
312
Welche Aussagen sind immer richtig?
x + y = 100 (x und y sind natürliche Zahlen)
313
■
Aussage A:
x≠y
■
Aussage B:
Es gibt mehr als eine Lösung.
■
Aussage C:
x < 100
■
Aussage D:
Wenn x gerade ist, ist auch y gerade.
Welche Aussagen sind immer richtig?
x · y = 2 500 (x und y sind natürliche Zahlen)
■
Aussage A:
x oder y ist grösser als 49.
■
Aussage B:
Es gibt mehr als eine Lösung.
■
Aussage C:
x < 100
■
Aussage D:
Wenn x gerade ist, ist auch y gerade.
www.mathbuch.info
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
9 | 10
19
Summen und Produkte
mathbuch 1
314
LU 19
Arbeitsheft +
A519-01
weitere Aufgaben «Grundanforderungen»
Welche Aussagen sind immer richtig?
x : y = 4 (x und y sind natürliche Zahlen)
■
Aussage A:
x ist 4-mal so gross wie y.
■
Aussage B:
x ist gerade.
■
Aussage C:
y ist gerade, wenn x Vielfaches von 8 ist.
■
Aussage D:
y ist gerade.
www.mathbuch.info
Als Kopiervorlage freigegeben
© Schulverlag plus AG / Klett und Balmer Verlag AG, 2013
10 | 10