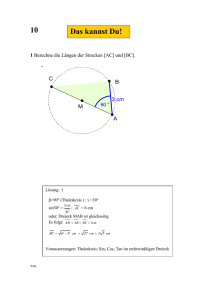
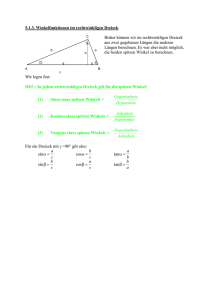
Trigonometrie - die Grundlagen in einem Tag

Trigonometrie die Grundlagen in einem Tag
Fachtage Dezember 2012
an der Kantonsschule Zürich Nord
Klasse W3n
R. Balestra
Name:
Vorname:
6. Dezember 2012
Inhaltsverzeichnis
1 Zielsetzung & Ablauf
1
2 Warum Trigonmetrie
2.1 Die Grenzen der bisherigen Geometrie . . . .
2.2 Über die Ähnlichkeit
zu den Definitionen im rechtwinkligen Dreieck
2.3 Zwei exakt berechenbare Werte . . . . . . . .
2.4 Der Einsatz des Taschenrechners . . . . . . .
. . . . . . . . . . .
2
2
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . .
3
5
6
3 Standardaufgaben
7
4 Exakt bestimmbare Werte
9
5 Trigonometrie am Einheitskreis
10
5.1 Definitionen am Einheitskreis . . . . . . . . . . . . . . . . . . . . 10
6 Die Graphen der trigonometrischen Funktionen
I
15
1
Zielsetzung & Ablauf
Die Ziele dieses Fachtages sind . . .
• die Trigonometrie im rechtwinkligen Dreieck kennenzulernen.
Wir werden dazu den Begriff Trigonometrie erklären,
aufzeigen, dass wir ohne Trigonometrie schon bei einfachen geometrischen
Problemen nicht weiterkommen und
den Einfluss der Ähnlichkeit auf den Sinn der Definitionen besprechen.
• die Trigonometrie am Einheitskreis zu besprechen.
Wir werden den durch das rechtwinklige Dreieck beschränkte Definitionsbereich von ]00 , 900 [ vergrösseren und werden dazu die trigonometrischen
Beziehungen neu am Einheitskreis definieren,
dabei aufzeigen, dass die Definitionen im rechtwinkligen Dreieck immer
noch Gültigkeit haben,
die ersten trigonometrischen Beziehungen kennenlernen und
mit der graphischen Darstellung der trigonometrischen Funktionen abschliessen.
Der Ablauf dieses Fachtags . . .
• wir beginn um 8:30
• und beenden den Tag, wenn wir fertig sind,
• es wird zwei grössere Theorieblöcke geben,
• und viel Arbeit, die ihr in Gruppen zu erledigen habt,
• die Pausen richten sich nach dem Stand der aktuellen Arbeiten.
1
2
2.1
Warum Trigonmetrie
Die Grenzen der bisherigen Geometrie
Eine kurze Begriffserklärung:
In der Trigonometrie (von griechisch trigonon - Dreieck und métron - Mass)
werden wir uns mit der Berechnung von Seiten und Winkeln in einem Dreieck
befassen.
Im Falle eines rechtwinkligen Dreiecks lassen sich mit Hilfe des Satzes von
Pythagoras einige Aufgaben exakt lösen:
Beispiel 2.1 In einem rechtwinkligen Dreieck ∆ABC sind die Länge der
Hypotenuse c = 6 und die Länge einer Kathete b = 3.7
bekannt.
Berechne die Länge der zweiten Kathete und die Höhe des
Dreiecks ∆ABC.
Doch schon für die Bestimmung der Winkelöffnungen sind wir auf wenig
genaue Hilfsmittel angewiesen:
Auch die Möglichen den Satz des Pythagoras anzuwenden sind nicht immer
gegeben:
Beispiel 2.2 In einem rechtwinkligen Dreieck ∆ABC sind die Länge der
Kathete a = 5.5 und die Öffnung des Winkels α = 630
bekannt.
Berechne die Längen der übrigen Seiten und die Grösse des
fehlenden Winkels.
2
2.2
Über die Ähnlichkeit
zu den Definitionen im rechtwinkligen Dreieck
Wir beginnen mit den trigonometrischen Beziehungen im rechtwinkligen Dreieck
und untersuchen dazu die folgenden Dreiecke auf Gemeinsamkeiten:
Was haben die folgenden Dreiecke gemeinsam ?
3
Wir fassen zusammen:
Def.:
In einem rechtwinkligen Dreieck ∆ABC mit den üblichen Bezeichnungen werden die trigonometrischen Funktionen wie folgt
definiert:
sin α :=
cos α :=
tan α :=
Bem.:
• sin β :=
• cos β :=
• tan β :=
. . . und wir können schon die ersten Beziehungen zwischen sin und cos (in
einem rechtwinkligen Dreieck) formulieren:
4
2.3
Zwei exakt berechenbare Werte
Berechne sin 300 :
Berechne tan 300 :
5
2.4
Der Einsatz des Taschenrechners
Aufgaben :
Bestimme mit dem Taschenrechner die folgenden
Werte:
1. den Sinus von 130 , 76.50 , 658290 ,
2. den Cosinus von 770 , 43.90 , −540 ,
3. den Tangens von 20 , 37.880 ,
4. den Winkel mit dem zugehörigen Sinuswert
0.8, 0.2, −0.6,
5. den Winkel mit dem zugehörigen Cosinuswert
0.8, 0.2, 2.1,
6. den Winkel mit dem zugehörigen Tangenswert
0.8, 0.2, 2.1.
6
3
Standardaufgaben
Für die folgenden Aufgaben arbeiten wir in einem rechtwinkligen Dreieck ∆ABC
mit den üblichen Bezeichnungen.
Aufgaben :
• Geg: c = 56.4 ∧ α = 38.50
Ges.: a, b
• Geg: a = 148.2 ∧ β = 38.50
Ges.: b, c
7
• Geg: a = 10.74 ∧ b = 6.48
Ges.: α, c, β h, p, q
WERKSTATT 1
8
4
Exakt bestimmbare Werte
Wir sind in der Lage, die folgenden Werte exakt zu berechnen:
α
00
300
450
600
sin
...
...
...
...
...
cos
...
...
...
...
...
tan
...
...
...
...
...
WERKSTATT 2
9
900
5
Trigonometrie am Einheitskreis
In diesem Abschnitt werden wir den Einheitskreis einführen und an ihm die
trigonometrischen Beziehungen neu definieren.
Wir werden ihn als praktisches Hilfsmittel kennenlernen und festellen, . . .
• dass die bisherigen Definitionen (im rechtwinkligen Dreieck) weiterhin
Gültigkeit haben,
• dass wir die trigonometrischen Funktionen nicht nur auf Winkel zwischen
00 und 900 anwenden können
und
• dass es viele interessante Beziehungen zwischen den trigonometrischen
Funktionen gibt, die wir nicht auswendig lernen müssen, wenn wir mit
dem Einheitskreis umgehen können.
5.1
Definitionen am Einheitskreis
Der Einheitskreis:
Def.:
cos ϕ := x-Koordinate von P
sin ϕ := y-Koordinate von P
tan ϕ := Quotient der y- & der x-Koordinate von P
10
Einige Beispiele:
11
Verwende zur Lösung der folgenden Aufgaben den Einheitskreis:
Aufgaben :
ϕ
00
900
1800
2700
sin
...
...
...
...
...
cos
...
...
...
...
...
tan
...
...
...
...
...
Wir können feststellen . . .
und wollen weiter noch festhalten:
12
3600
Mit Hilfe des Einheitskreises lassen sich viele Beziehungen und Eigenschaften der trigonometrischen Funktionen erkennen:
• Für welche Winkel ist der sin-Wert negativ ?
• Für welche Winkel ist der cos-Wert > 0, 5 ?
• Für welche Winkel ist der tan-Wert positiv ?
13
• Für welche Winkel erhalten wir den selben sin-Wert ?
• Für welche Winkel erhalten wir den selben cos-Wert ?
WERKSTATT 3
14
6
Die Graphen der trigonometrischen Funktionen
Die graphischen Darstellungen von sin, cos & tan:
• für den Sinus:
15
• für den Cosinus:
• für den Tangens:
16