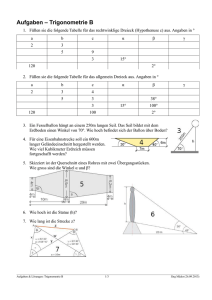
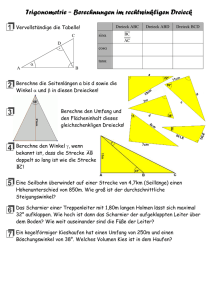
10II - SINUS transfer

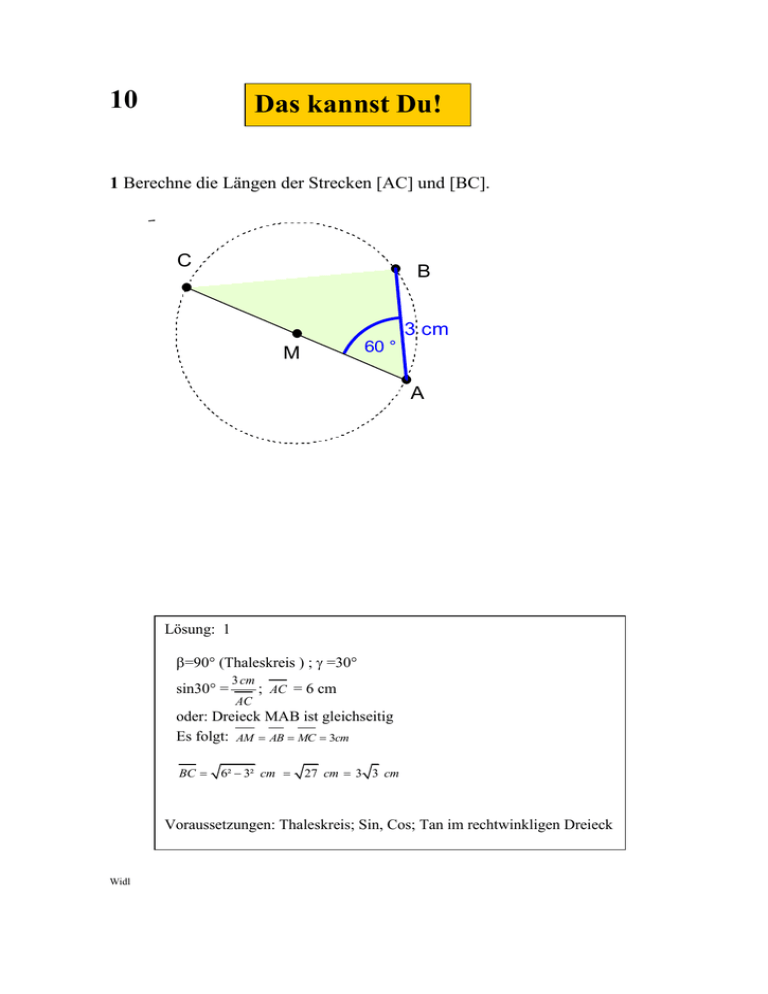
10
Das kannst Du!
1 Berechne die Längen der Strecken [AC] und [BC].
C
B
60 °
M
3 cm
A
Lösung: 1
=90° (Thaleskreis ) ;  =30°
sin30° =
3 cm
; AC = 6 cm
AC
oder: Dreieck MAB ist gleichseitig
Es folgt: AM  AB  MC  3cm
BC 
6²  3² cm 
27 cm  3 3 cm
Voraussetzungen: Thaleskreis; Sin, Cos; Tan im rechtwinkligen Dreieck
Widl
C
10
B
60 °
Das kannst
Du!
M
3 cm
A
1 Es gilt: sin 53,13° = 0,8
Berechne die Länge der Strecke [AC].
C
53,13 °
150 °
A
8 cm
B
Lösung: 1
=30°
AC
sin 30

8cm
sin 53,13
; AC 
Voraussetzungen: Sinussatz
Widl
8 0, 5
0, 8
cm ; AC = 5 cm
10
Das kannst Du!
Unter welchem Winkel steht die Sonne über dem
Horizont, wenn der Schatten des 1,90 m
breiten Balkons ein Drittel der Wand
bedeckt?
Balkon
Hinweise:
sin  = 0,578 ;  = 35,3°
cos  = 0,578 ;  = 54,7°
tan  = 1,73 ;  = 59,9°
3,30 m
Lösung:
Das "Schattendreieck" unterhalb des Balkons ist rechtwinklig 
tan  =
1,90
; tan  = 1,73 ;  = 59,9°
1
 3,30
3
Winkel über dem Horizont: 90° – 59,9° = 30,1° also ca. 30°
Voraussetzungen: Sinus, Kosinus, Tangens im rechtwinkligen Dreieck
Christine Pichler
10
Das kannst Du!
1 Wie weit ist der Gipfel des Wendelsteins von unserer Schule entfernt?
Um diese Frage zu klären, misst eine Schülergruppe mit einem einfachen
Winkelmessgerät einen Winkel von 4° zwischen der Horizontalen und dem
Gipfel des Wendelsteins. Aus einer Wanderkarte entnehmen sie, dass
Rosenheim auf 446 m ü NN liegt und der Wendelstein 1838 m hoch ist.
Hinweis:
tan 4° = 0,0699;
cos 4° = 0,9976
sin 4° = 0,0698
Lösung: Geeignete Skizze; einige Schüler berechnen eventuell die horizontale
Entfernung – Vergleich und Diskussion der Ergebnisse
sin 4° = Error!  s = Error! = 19955 m;
sinnvoll gerundet: 20 km
Voraussetzungen: Winkelberechnung im rechtwinkligen Dreieck
Thanhäuser Roland
10
Das kannst Du!
1. Wie hoch ist der Bodensee?
Info: Der Bodensee ist 60 km lang!
2. Wie hoch müsste in Bregenz ein Turm sein, wenn man auf der
anderen Seite des Bodensees (60 km entfernt) am Ufer steht und
die Spitze noch sehen kann?
Nach PM Dezember 2005
Lösung: 1. Frage diskutieren! Geeignete Skizze
wie nebenstehend ev. im U-Gespräch erarbeiten
x² = 6370²  30²  x = 6369,929 km  h = 71 m
Diskussion: Lösung eigentlich nicht ganz korrekt,
da die 60 km auf dem Bogen liegen!
In 10. Kl.: Error!  360°  = 0,54°
cos 0,27° = Error!  x = 6369,929 km  h = 71 m
Vergleich der Ergebnisse!
h
30
6370
x

2.Vgl. „Wie weit ist der Horizont?“
s1 = 4,65km  s2 = 55,35 km
r2² = 6370²  55,35²  r2 = 6370,240 km  h2 = 240 m
h2
s2
s1
h1
Voraussetzungen: Tangente an Kreis
Pythagoras
In 10. Kl.: Kreisbogen
Winkelberechnung im rechtwinkligen Dreieck
Hinweis: GTR ausnahmsweise erlaubt!
Thanhäuser Roland