Trigonometrie B

Aufgaben – Trigonometrie B
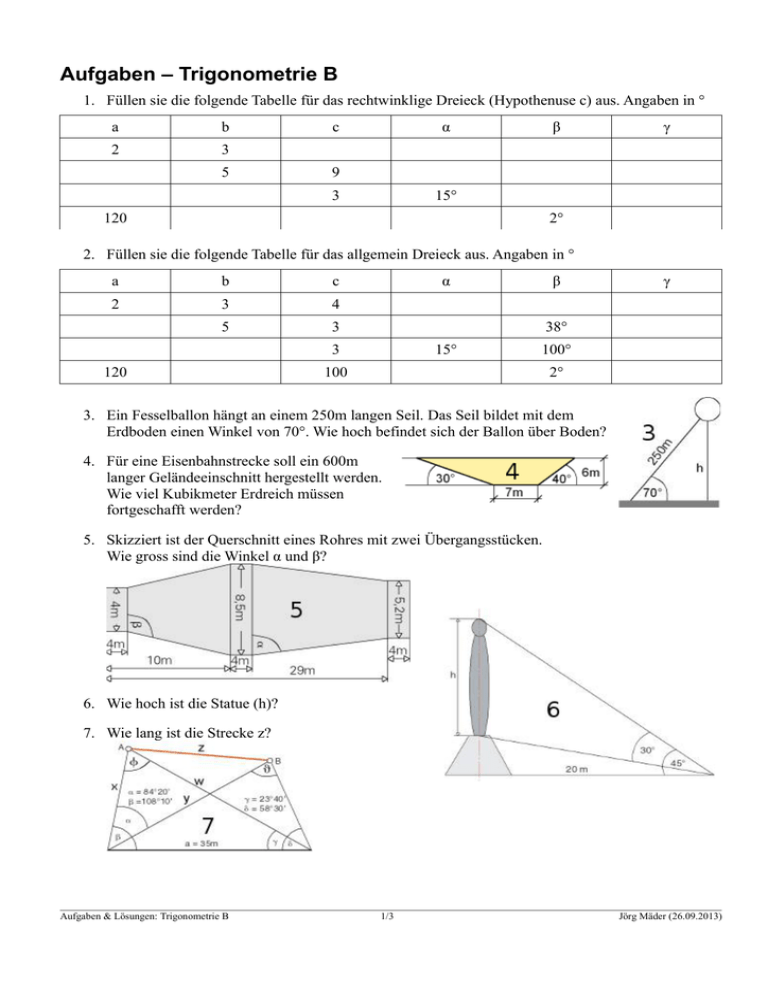
1. Füllen sie die folgende Tabelle für das rechtwinklige Dreieck (Hypothenuse c) aus. Angaben in °
a
b
2
3
5
c
α
β
γ
9
3
15°
120
2°
2. Füllen sie die folgende Tabelle für das allgemein Dreieck aus. Angaben in °
a
b
c
2
3
4
5
3
α
γ
38°
3
120
β
15°
100°
100
2°
3. Ein Fesselballon hängt an einem 250m langen Seil. Das Seil bildet mit dem
Erdboden einen Winkel von 70°. Wie hoch befindet sich der Ballon über Boden?
4. Für eine Eisenbahnstrecke soll ein 600m
langer Geländeeinschnitt hergestellt werden.
Wie viel Kubikmeter Erdreich müssen
fortgeschafft werden?
5. Skizziert ist der Querschnitt eines Rohres mit zwei Übergangsstücken.
Wie gross sind die Winkel α und β?
6. Wie hoch ist die Statue (h)?
7. Wie lang ist die Strecke z?
Aufgaben & Lösungen: Trigonometrie B
1/3
Jörg Mäder (26.09.2013)
8. (schwer) Man beobachtet einen Ballon vom Festland aus
unter einem Winkel von 21,88°. Sein Spiegelbild im Wasser
erblickt man unter einem Winkel von 38,28°. Der
Wasserspiegel liegt 48,5m unterhalb des Aussichtpunktes.
Wie hoch liegt der Ballon über dem Festland (b)?
Aufgaben & Lösungen: Trigonometrie B
2/3
Jörg Mäder (26.09.2013)
Lösungen – Trigonometrie B
1. Füllen sie die folgende Tabelle für das rechtwinklige Dreieck (Hypothenuse c) aus. Angaben in °
a
b
c
α
β
γ
2
3
3.61
33.7°
56.3°
90°
7.48
5
9
56.3°
33.7°
90°
0.776
2.89
3
15°
75°
90°
120
4.19
120.07°
88°
2°
90°
2. Füllen sie die folgende Tabelle für das allgemein Dreieck aus. Angaben in °
3.
a
b
c
α
β
γ
2
3
4
29.0°
46.6°
104°
7.01
5
3
120.3°
38°
21.7°
0.857
3.26
3
15°
100°
65°
120
20.4
100
168.1
2°
9.869°
h=250⋅sin(70 ° )=235
4. Am besten unterteilt man das Trapez in ein Rechteck in der Mitte
6
6
=10.39 b=
=7.15
und zwei Dreiecke. a=
tan( 30)
tan( 40)
a⋅6
b⋅6
A=
+6⋅7+
=94.62 V = A⋅600=56'800
2
2
5.
8.5−4
2
β=atan
+90 ° =110.6 °
10−4
( )
α=atan
(
29−10−4
=83.7
8.5−5.2
2
6. g: Gesamthöhe; s: Sockelhöhe
g=20⋅tan(45 °)=20 s=20⋅tan(15 °)=5.36m
7.
)
h=g−s=14.64m
φ=180−β−γ=48.17 ° ϑ=180 ° −δ−(β−α)=97.67°
x sin ( γ)
y sin (δ)
z= √ x 2+ y 2−2⋅x⋅y⋅cos (α)=37.1
=
→ x=18.86
=
→ y=30.11
a sin( φ)
a sin(ϑ)
8. Am besten sucht man mehrere Gleichungen für ein Gleichungssystem
b+48.5=c
b
b=100.5
tan(21.88° )=
→ c=149.0
h
h=250.3
c+48.5
tan(38.28° )=
h
{
Aufgaben & Lösungen: Trigonometrie B
3/3
Jörg Mäder (26.09.2013)