Sinus, Cosinus Tangens am rechtwinkligen Dreieck

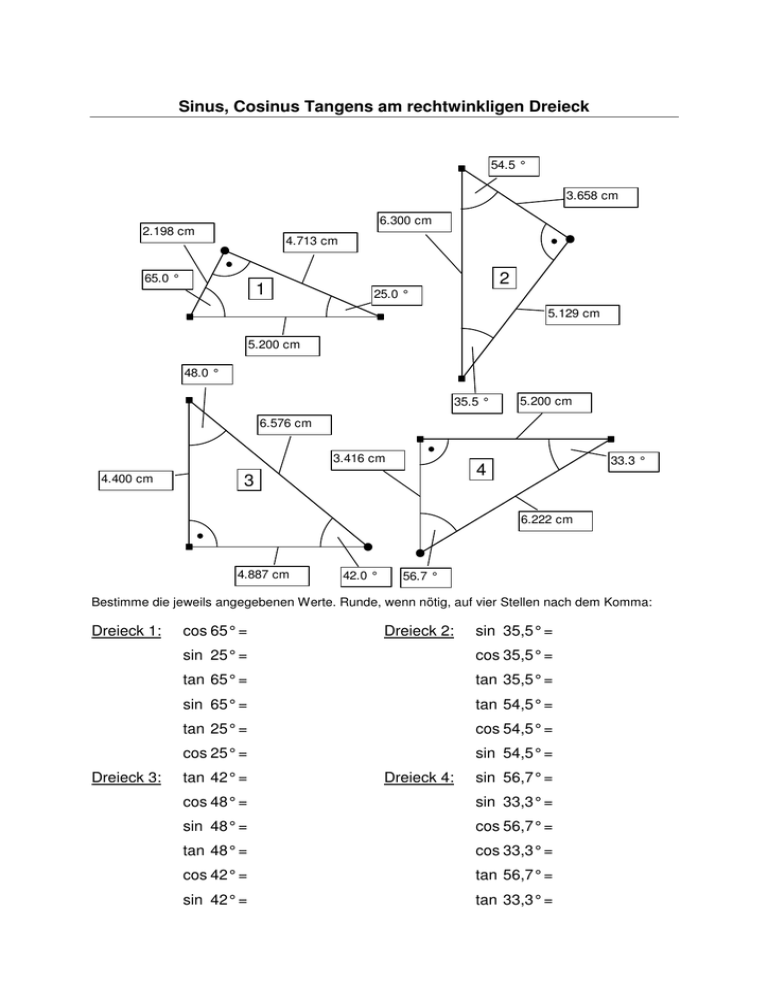
Sinus, Cosinus Tangens am rechtwinkligen Dreieck
54.5 °
3.658 cm
6.300 cm
2.198 cm
4.713 cm
65.0 °
1
2
25.0 °
5.129 cm
5.200 cm
48.0 °
35.5 °
5.200 cm
6.576 cm
3.416 cm
4.400 cm
33.3 °
4
3
6.222 cm
4.887 cm
42.0 °
56.7 °
Bestimme die jeweils angegebenen Werte. Runde, wenn nötig, auf vier Stellen nach dem Komma:
Dreieck 1:
Dreieck 3:
cos 65° =
Dreieck 2:
sin 35,5° =
sin 25° =
cos 35,5° =
tan 65° =
tan 35,5° =
sin 65° =
tan 54,5° =
tan 25° =
cos 54,5° =
cos 25° =
sin 54,5° =
tan 42° =
Dreieck 4:
sin 56,7° =
cos 48° =
sin 33,3° =
sin 48° =
cos 56,7° =
tan 48° =
cos 33,3° =
cos 42° =
tan 56,7° =
sin 42° =
tan 33,3° =
Berechne die fehlenden Seiten und Winkel des jeweiligen Dreiecks. Überprüfe dann die gefundenen
Werte durch nachmessen an der Zeichnung:
C
α =
β =
γ = 90°
b =
p =
q =
hc =
<BCD =
<ACD =
2.809 cm
A
B
6.500 cm
α = 90°
β =
γ =
a =
b =
c =
ha =
<DAB =
<CAD =
CD =
C
0.686 cm
B
A
1.936 cm
C
α =
β = 90°
γ =
a =
b =
hb =
<CBD =
<DBA =
AD =
CD =
3.954 cm
A
6.600 cm
B