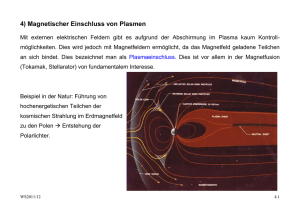
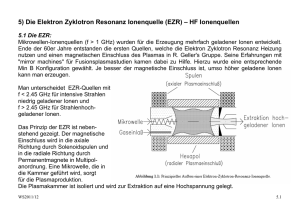
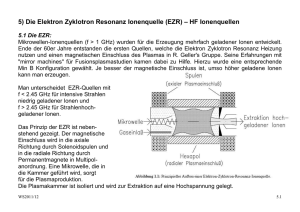
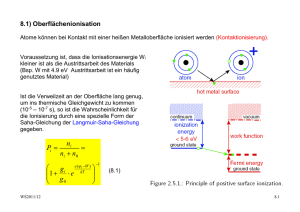
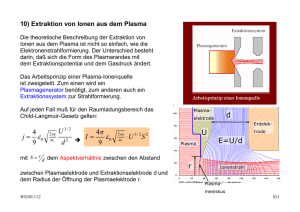
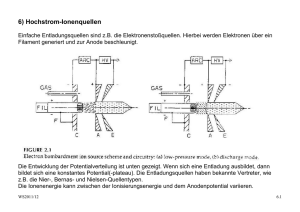
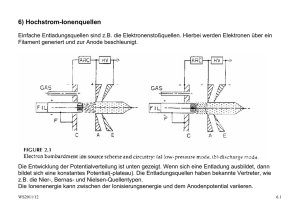
3.1) Grundlagen der Plasmaphysik für Ionenquellen

3.1) Grundlagen der Plasmaphysik für Ionenquellen
Zum Verständnis der Ionenquellen ist Wissen aus der Plasmaphysik erforderlich.
Die Zusammensetzung eines Plasmas ist je nach Ionisierungsgrad ein Gemisch aus
Ionen, Elektronen und Atome (neutralen Teilchen)
Im Gegensatz zu einem Gas besteht zwischen den Teilchen im Plasma eine starke Interaktion
aufgrund der Coulombkräfte. Das Verhalten eines Plasmas kann durch elektrische und magnetische
Felder beeinflusst werden.
Oft wird der Plasmazustand auch als „vierter Aggregatzustand“ der Materie bezeichnet! Jedoch liegt
beim Übergang vom Gas zum Plasma kein Phasenübergang im thermodynamischen Sinne vor. Man
benötigt jedoch Energie (wie latente Wärme), um die Atome in einem Gas zu ionisieren!
Beispiele für Plasmen:
natürliche:
Sonne, Ionosphäre, Polarlichter, Flammen, Blitze, e- in Metallen
künstliche:
Neonröhren, Plasmabildschirme, Plasma-Ätzanlagen,
Fusionsplasmen, Metall-Dampflampen, Ionenquellenplasmen
Aufgrund der freien Ladungsträger, besitzt ein Plasma eine hohe Leitfähigkeit!
WS2011/12
3.1
Plasmadichte und Plasmatemperatur
Unter der Ionen- oder Elektronendichte des Plasmas versteht man die Teilchendichte
ni
und ne
⎡ 1 ⎤
⎢⎣ cm 3 ⎥⎦ oder
in
⎡ 1 ⎤
⎢⎣ m 3 ⎥⎦
In einem Mehrkomponentenplasma gilt das Prinzip der Ladungsneutralität:
∑ q ⋅n
i
i
= ne
(3.1)
Der Ionisierungsgrad eines Plasmas ist definiert als
pion =
ni
ni + nneutral
Für pion = 1 spricht man von einem vollständig ionisiertem Plasma.
Man spricht von einem hochionisiertem Plasma, wenn der Ionisierungsgrad größer 10% wird.
typische Laborplasmen: ne ~ 1014 – 1022 1/m3
Zum Vergleich, Gasdichte bei Raumtemperatur und 10-2 Pa: n = 2.5*1018 1/m3
WS2011/12
3.2
Die Temperatur von Plasmen wird gewöhnlich in eV angegeben:
1 eV = 11600 K
e*U = kT Æ U = 1 V Æ T = e/k
Ionentemperatur Ti und Elektronentemperatur Te müssen nicht identisch sein. Ist ein Magnetfeld
vorhanden, so wird eine Anisotropie eingeführt, die zu unterschiedlichen T parallel und senkrecht zum
Magnetfeld führt:
Î
Ti|| , Ti ⊥ , Te|| , Te ⊥
Der Grund liegt in der unterschiedlichen Mobilität der Teilchen parallel und senkrecht zum Magnetfeld.
Der Temperaturbegriff wird auch auf Plasmen angewendet, die noch nicht im thermischen
Gleichgewicht sind!
typische Elektronentemperaturen:
• Oberflächenionisierte Plasmen
• Bogenentladungen
• Mikrowellen generierte Plasmen
WS2011/12
Te ~ 0.2 eV
Te ~ 1 eV
Te ~ mehrer keV
Ti < 1 eV
3.3
Plasmafrequenz
In Plasmen können sowohl die Elektronen wie auch die Ionen Schwingungen vollführen. Je nach
Komponenten hat man unterschiedliche Schwingungsmoden vorliegen. Die ElektronenplasmaOszillationen (Langmuirwellen) oder der „Ionenschall“.
Kontinuitätsgleichung:
r
∂ρ
+ div j = 0
∂t
r
r
j = ρ ⋅ v , ρ = n e ⋅ me
Bewegung des Plasmas folgt aus der Eulerschen Gleichung (hydrodynamische Bewegungsgleichung
für inkompressible, reibungsfreie Strömung)
r
r r
∂
v
⎛
ρ ⋅⎜ + v ⋅∇
⎝ ∂t
r
r⎞
dv r
v⎟ =ρ⋅
=F
dt
⎠
( )
mit
r
r
F = − ne eE
Aufteilen der Ladungsträgerdichte ne in einen konstanten Anteil ne0 und eine Störung ne1 mit
ne 0 >> ne1
, wobei ne1 nicht neutralisiert ist!
Aufgrund der Quasineutralität ist
WS2011/12
ρ el = −e ⋅ ne 0 + ∑ qi ni 0 − e ⋅ ne1 = −e ⋅ ne1
i
3.4
Aus der 1. Maxwell Gleichung folgt
Annahme:
r
r
v , ne1 und E
r
∂v
e r
=−
E
∂t
me
r ρ el
e ⋅ ne1
div E =
=−
ε0
ε0
sind sehr kleine Größen. Dann folgt (Linearisierung der Gleichungen):
aus der Eulerschen Gleichung und
r
∂ne1
+ ne 0 ⋅ div v = 0
∂t
aus der
Kontinuitätsgleichung.
Mit beiden Gleichungen erhält man:
∂ 2 ne1
e 2 ne1
+ ne 0
=0
2
∂t
meε 0
Î
Schwingungsgleichung mit
e 2 ⋅ ne 0
ω =
me ⋅ ε 0
2
p
(3.2)
ne1 (t ) = A ⋅ cos ω p t
Plasmafrequenz
1/ωp ist die charakteristische Zeit, in der das Plasma auf eine Störung reagiert!
WS2011/12
3.5
1
fp =
2π
WS2011/12
e2
⋅ ne = 8,98 ⋅ ne [ m13 ][Hz ]
ε 0me
3.6
Nur elektromagnetische Wellen mit f > fp können durch das Plasma laufen. Man nennt ωp oder fp daher
auch die cut-off-Frequenz des Plasmas.
Dass die Störung im Plasma nur klein sein kann, zeigt die Berechnung des elektrischen Feldes aus
einer Störung der Quasineutralität um 1% in einer lokalen Umgebung der Größe von 1 mm:
r ρ
div E =
ε0
⇒
V
δE 0.01 ⋅ ne ⋅ e
≈
⇒ δ E ≈ 1010
δx
ε0
m
Ein solches Feld würde nicht aufrechterhalten werden. Daher gilt die Quasineutralität, bis auf winzige
Störungen, sehr genau. Die Elektronendichte, bei der eine elektromagnetische Welle der Frequenz fp
gerade reflektiert wird, ist die kritische Dichte
nkritisch
4π 2ε 0 me 2
2⎡ 1 ⎤
=
⋅ f p = 0.0124 ⋅ ( f p [Hz ]) ⎢ 3 ⎥
e2
⎣m ⎦
Beispiele für cut-off-Frequenzen:
• freie Elektronen in Metallen, Dichte ~1028 1/m3 Æ f ~ 1015 Hz, sichtbares Licht wir reflektiert, UVLicht wird durchgelassen
• Ionosphäre, Dichte ~109 – 1010 1/m3 Æ f ~105 –106 Hz, d.h. Mittelwelle wird reflektiert, UKW wird
durchgelassen
WS2011/12
3.7
Die Debye-Länge
Die Quasineutralität bewirkt eine Abschirmung der Plasmateilchen untereinander. Wie groß der
Bereich der Abschirmung ist, kann durch eine Störungsrechnung ermittelt werden:
r
r
v
v
ne (r ) = ne + ne1 (r ) ; ni (r ) = ni + ni1 (r )
Ausgangspunkt:
Poissongleichung
∆φ = −
r
r
ρ
1
= − [− e ⋅ ne + Ze ⋅ ni − e ⋅ ne1 (r ) + Ze ⋅ ni1 (r )]
ε0
ε0
Unter der Annahme einer thermischen Gleichgewichts (Te=Ti und Boltzmannverteilung)
r
r
φ
(
)⎤
e
r
⎡
ne1 (r ) = ne ⋅ exp ⎢
⎥
⎣ kT ⎦
,
r
r
φ
(
)⎤
Ze
r
⎡
ni1 (r ) = ni ⋅ exp ⎢
⎥
⎣ kT ⎦
(3.3)
und Quasineutralität erhält man eine durch Linearisierung von (3.3) und Einsetzen in die
Poissongleichung:
r e 2 ⋅ ne ⎡ 1
Z ⎤ r
ρ0
(
)
∆φ (r ) −
+
r
φ
=
−
ε 0 ⎢⎣ kTe kTi ⎥⎦
ε0
WS2011/12
3.8
Lösung
r
φ (r ) =
r
q − λD rˆ
⋅ e ⋅r
4πε 0 r
1
Î
λ2D =
für
r
r
ρ 0 (r ) = q ⋅ δ ( r )
(eine Ladung q)
ε 0 ⋅ k ⋅ Te
ne ⋅ e 2
(3.4)
Debye-Länge
Die Debye-Länge (hier für Elektronen) ist die charakteristische Länge für die Abschirmung der
Ladungen der konstanten Hintergrunddichte ρ0.
Die Lösung der obigen DGL ist
das Coulombpotential mit Abschirmung.
Den Verlauf der Funktion zeigt die
nachfolgende Graphik.
Für r > λD fällt das Potential
exponentiell ab.
Jedes geladene Teilchen ist
von einer Debye-Wolke umgeben.
WS2011/12
3.9
Praktische Berechnung
der Debye-Länge:
λD =
ε 0 ⋅ k ⋅ Te
ne ⋅ e 2
λD = 7437
WS2011/12
Te [eV ]
[m]
1
ne [ m 3 ]
3.10
Plasmarand und Plasmapotential
Ein Plasma erschein auf der Größenordnung x > λD als quasineutral. Das Potential im Inneren ist
konstant bezüglich des äußeren Wandpotentials. Das Potential des Plasmas bezüglich der Wand φp
nennt man Plasmapotential. Nun könnten die Plasmateilchen an der Wand elastisch reflektiert werden,
dann entspräche φp dem Wandpotential. Die Teilchen rekombinieren mit 99% Wahrscheinlichkeit!
Plasma-Wand Grenzschichten: a) ideal reflektierend , b) vollständige
Wandrekombination
WS2011/12
3.11
Der Fluss auf die Wand ergibt sich aus der Maxwellschen Geschwindigkeitsverteilung:
⎛ m ⎞
dW = f ( v )d 3v = ⎜
⎟
2
π
kT
⎝
⎠
mittlere Geschwindigkeit:
3/ 2
⎛ mv 2 ⎞ 3
⎟⎟d v
exp⎜⎜ −
⎝ 2kT ⎠
v = ∫ v f ( v ) d 3v =
Anzahl der Teilchen mit
r r
r
v ∈ [v , v + dv ]
8kT
πm
Der Fluss auf die Wand ist damit
1/ 2 ∞
⎛ m ⎞
Γ = n⎜
⎟
2
π
kT
⎝
⎠
nv
⎛ mv 2 ⎞
⎜
⎟
v
exp
dv
−
=
∫0 x ⎜⎝ 2kT ⎟⎠ x 4
Damit ist der Fluss proportional zur mittleren Geschwindigkeit der Teilchen. Daher gilt
Γe =
mi
Γi
me
Da die Geschwindigkeit und damit der Fluss der Elektronen größer ist im Vergleich zu den Ionen,
würde sich ein Strom ausbilden, der die Quasineutralität bricht. Daher lädt sich die Wand negativer
ggü. dem Plasma oder das Plasma positiver ggü. der Wand auf.
WS2011/12
3.12
Dadurch werden die Elektronen abgebremst und die Ionen beschleunigt, was die Nettoflüsse
ausgleicht. Es bildet sich eine Ladungsträgerdoppelschicht, die in der Größenordnung einiger DebyeLängen liegen kann. Man nennt diese die Debye-Schicht.
Die Schichtdicke des Plasmarandes hängt natürlich vom Potential einer eventuellen Zugelektrode ab
mit φ >> φp.
Dann gilt
d sheath = λD ⋅
e ⋅ φ Zug
kT
(3.5)
was mit
ne = 1018 1/m3, Te = 1 eV, λD = 10 µm
und φZug = 20000 V
einen Wert von dsheath = 1.4 mm ergibt.
Eine isoliert aufgehängte Elektrode im Plasma wird sich auf ein „floating potential“ φf aufladen das ca.
3-4 mal kTe entspricht. Für diese gilt Γe
WS2011/12
= Γi , d.h. es gibt keinen Nettostrom.
3.13
Mit einer Sonde, die in das Plasma
hinein ragt und mit einer Spannungsquelle
versorgt wird, kann man die Potentiale
ermitteln. Eine solche Sonde nennt man
Langmuir-Sonde.
Variiert man das Potential zwischen Sonde
und Wand, so erhält man eine charakteristische
Strom-Spannungskennlinie!
Die Sättigungsströme sind den Flüssen proportional:
I e,sat
mi
=
I i ,sat
me
d (ln I p )
,
dV
=
1
T( eV )
,
ne =
4 I e , sat
e ⋅ Aprobe T( eV )
In der Praxis limitiert der Leistungsfluss zur Sonde den Einsatzbereich.
WS2011/12
3.14
3.2) Erzeugung von Quellenplasmen
Erzeugung eines quasineutralen Plasmas durch Stoßionisation
∑q n
i i
= ne
Bereitstellung freier Atome im
Plasmagenerator durch:
Bereitstellung freier Elektronen
durch:
Bereitstellung der Ionisationsenergie durch:
• Einlassen eines Arbeitsgases
• Glühemission
• Beschleunigung der Elektronen
• Schmelzen und Verdampfen
• Photoionisation
• HF-Heizung
• Sputtern von Feststoffen
• Funkenentladung
• E x B-Drift
WS2011/12
3.15
Einfachstes Experiment zur Erzeugung eines Plasmas ist die Gasentladung. Dazu benötigt man eine
Vakuumröhre. Die nachfolgende Abbildung zeigt den einfachsten Aufbau eines Gasentladungsrohres.
Mit Absinken des Gasdrucks erkennt man eine Leuchterscheinung an der Kathode. Das neutrale Gas
ist dann zumindest teilweise in den Plasmazustand übergegangen (Gas ist leitfähig geworden).
WS2011/12
3.16
Im neutralen Gas werden spontan (z.B. durch
Röntgenquanten aus der natürlichen Strahlung)
Atome ionisiert und dadurch Elektronen freigesetzt.
Die Stärke des zwischen Anode und Kathode
gemessenen Stromes hängt davon ab wie viele
Ladungsträger das Elektron auf seinem Weg erzeugt.
Wahrschein lichkeit für Ionisation durch e α=
Weglänge
erster Townsendkoeffizient
zweiter Townsendkoeffizient β beschreibt die Ionisation eines Atoms durch ein Ion (ist in Plasmen zu
vernachlässigen). Für die entstandenen Elektronen gilt:
dN e
= α ⋅ Ne
dx
⇒
N e (d ) = N e 0eαd
Ne0 = Anzahl der erzeugten Elektronen an der Kathode
dN i
= β ⋅ Ni
dx
⇒
N i ( d ) = N i 0e βd
desgleichen für die Ionen
WS2011/12
3.17
Für αd >> 1 Æ N(d) >> N0
Ladungsträger oder Townsendlawine
Unterhalb eines gewissen Gasdrucks p entwickelt sich eine stationäre Entladung, d.h. Elektronen
werden kontinuierlich erzeugt. Stöße der Ionen mit dem Kathodenmaterial setzen Sekundärelektronen
frei. Die Zahl der pro Ion erzeugten Elektronen γ ist der dritte Townsendkoeffizient mit
WS2011/12
dN e = N i ⋅ γ
.
3.18
γ ≈ 0.01 − 0.1
Zündbedingung
γ ⋅ e αd ≥ 1
Mit der Zündbedingung ergibt sich für die Zündspannung:
Mit
U Zünd =
c2 p ⋅ d
ln (c1 p ⋅ d ) − ln (ln( γ1 ) )
λf = mittlere freie Weglänge im Gas, Ui = Ionisationspotential
(Zünd- oder Paschenkurve)
Für große p*d muß die geringere
freie Weglänge durch größeres U
kompensiert werden.
Für kleine p*d geht U Æ ∞, da die freie
Weglänge der Elektronen >> d wird.
Im Minimum der Kurve ist die
freie Weglänge ~ d.
Die Unterschiede zwischen den Kurven
beruhen auf dem elementspezifischen
Werten für den Sekundärelektronenkoeffizienten γ.
WS2011/12
3.19
Man spricht bei geringem Gasdruck von einer Glimmentladung und bei höherem Strom
und Gasdruck von einer Bogenentladung.
WS2011/12
3.20