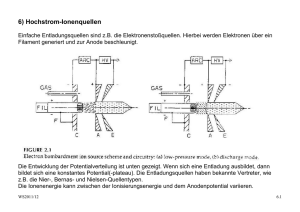
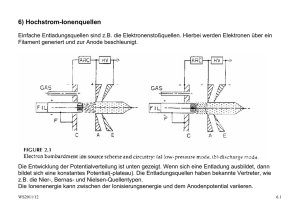
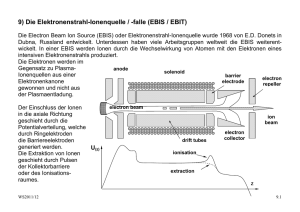
08_VSWS1112_surfaces..

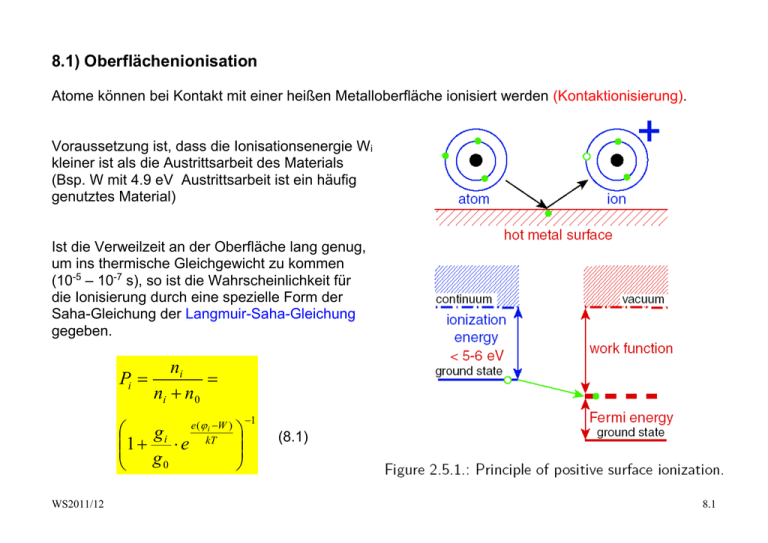
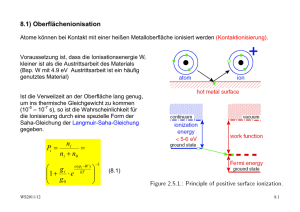
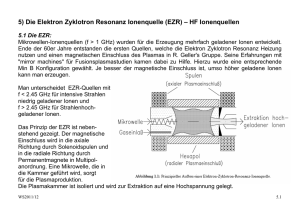
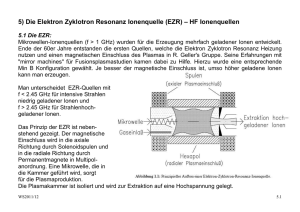
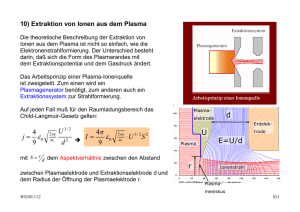
8.1) Oberflächenionisation
Atome können bei Kontakt mit einer heißen Metalloberfläche ionisiert werden (Kontaktionisierung).
Voraussetzung ist, dass die Ionisationsenergie Wi
kleiner ist als die Austrittsarbeit des Materials
(Bsp. W mit 4.9 eV Austrittsarbeit ist ein häufig
genutztes Material)
Ist die Verweilzeit an der Oberfläche lang genug,
um ins thermische Gleichgewicht zu kommen
(10-5 – 10-7 s), so ist die Wahrscheinlichkeit für
die Ionisierung durch eine spezielle Form der
Saha-Gleichung der Langmuir-Saha-Gleichung
gegeben.
Pi 
ni

ni  n 0
e ( i W )


gi
1   e kT 
 g

0


WS2011/12
1
(8.1)
8.1
Dabei sind gi und g0 das statistische Gewicht der Ionen und der Neutralteilchen, i ist das Ionisierungspotential (Ionisationsenergie) der neutralen Gasatome und W ist die Austrittsarbeit des Metalls der
heißen Oberfläche.
Der Anteil der Ionen ist für die meisten Kombinationen
i, W sehr klein, bis auf die Alkalimetalle.
Beispiel: K auf 2000 K (0.17 eV) heißes Pt
 i  4.5 eV , W Pt  5.65 eV
1
 1 ( 4.50.175.65) 
  0.9994
Pi  1   e

2


Beispiele für Ionisation auf Iridium zeigt
nebenstehende Graphik. Ein großer Vorteil
der Oberflächenionisierung ist die geringe
Energieverschmierung
der Ionen von W ~ 2kT << 1 eV.
Eine der wichtigsten Anwendungen:
Erzeugung von Cs-Ionen für Sputterquellen.
WS2011/12
8.2
Wie man aus der Saha-Langmuir-Gleichung erkennt, nimmt Pi mit zunehmendem T ab, wenn
 i W  0
ist.
T muss jedoch hoch genug sein, das das entsprechende Element evaporiert. Die Diffusion von
Oberflächenmaterial hingegen muss im Betrieb klein genug sein (< 10% einer Monolage), damit die
Ionisierungsbedingungen möglichst konstant bleiben.
WS2011/12
8.3
Im Gegensatz zu Plasma-Ionenquellen, bei denen die Extraktionsoptik von der Form des Plasmarandes abhängt, wird bei der Oberflächenquelle die Extraktion der Ionen durch die Form der heißen
Oberfläche bestimmt. Außerdem ist die Strahlformierung unabhängig von der Ionenstromdichte!
Neben Pellets werden auch Zeolite verwendet (Einlagerung des zu Ionisierenden Materials). Quellen
mit 75 mA Strahlstrom bei 2.5 cm Strahldurchmesser sind ohne weiteres machbar. Der Vorrat in den
Quellenkörpern bestimmt die Lebensdauer der Quelle.
Erhöhung der Effizienz: hot cavity als Ionisierer 
viele Kontakte mit den Wänden
 erhöht Pi
In einer solchen cavity können Elemente
mit i ~ 8 eV ionisiert werden.
Jedoch werden fast ausschließlich einfach
geladene Ionen produziert!
Die Oberflächenionisation wurde zuerst von Langmuir 1923 untersucht. Später wurden der Vorteil von
Oberflächenbelegung mit Sauerstoff und Cäsium (positive, bzw. negative Ionen) ersichtlich. Als
Oberflächen dienen überwiegend Wolfram, Iridium oder Rhenium.
WS2011/12
8.4
8.2) Produktion negativ geladener Ionen an Oberflächen
Die Produktion negativ geladener Ionen ist überwiegend exotherm, im Gegensatz zur Produktion
positiv geladener Ionen. Unterschied zu positiven Ionen: In großem Abstand praktisch kein
Coulombfeld
Das Elektron schafft sich durch Polarisation der neutralen Atome oder Moleküle selbst das binden
Potential. Negative Ionen können durch folgende Prozesse erzeugt werden:
 Volumenprozesse durch Elektronenstoß
 Umladung in Metalldämpfen
 Umladung an Oberflächen
Oberflächenumladung:
Nutzen der niedrigen Austrittsarbeit von heißen Metalloberflächen (wie bei Oberflächenionisierung
oder Sputterquellen)
Beispiel siehe Graphik
Cs Atome werden an einer heißen Oberfläche ionisiert und auf das Target beschleunigt. Dabei werden
Atome des Targetmaterial herausgeschlagen und negativ geladen, vor allem, wenn noch eine Cs
Oberflächenschicht aufgebracht wird.
Target kann schnell über ein Targetrad gewechselt werden (Graphik).
WS2011/12
8.5
Sputterquelle
WS2011/12
8.6
WS2011/12
8.7
Plasma-Oberflächen Konversion
Plasma wird vor dem Target generiert und das
Target auf negatives Potential gelegt.
Ionen aus dem Plasma sputtern negative Ionen
aus dem Material
Die Produktion negativer Ionen ist besonders
effizient, wenn das Atom die Metalloberfläche
mit v verlässt, das etwas größer ist als die
thermische Geschwindigkeit. Das Elektron
wird während des Ejektionsprozesses übertragen.
(siehe Graphik)
Ein Beispiel für die Produktion negativer Ionen
an einem Mg-Target zeigt die nachfolgende
Graphik.
WS2011/12
8.8
Der negative Ionenstrom ergibt sich zu
I   I   A   exp  n0 L d 
WS2011/12
I+ = positiver Ionenstrom, A = Sputterrate,
- = Produktionseffizienz für negative Ionen an der Oberfläche
no = Restgasdichte, L = Fluglänge durch das Restgas
d = Umladungsquerschnitt
8.9
8.3) Laser-Plasmaionenquellen
Im Unterschied zur resonanten Ionisation wird bei dieser Quelle ein Plasma durch die
Energiedeposition erzeugt. Die Laserstrahlung dringt so tief in das Material ein bis
f Laser  f cutoff .
 Lokale Heizung von Elektronen via inverser Bremsstrahlung + Anregung von Atomen
 Material wird abliert und es entsteht eine expandierende Plasma Plume
Ist die Plasmadichte so weit abgefallen, dass die cut-off Frequenz unter die Laserfrequenz fällt, dann
kann das Laserlicht wieder eindringen. Dadurch werden die Elektronen im Plasma bis zu 100 keV
beschleunigt.
 hochgeladenen Ionen, wobei
(Te = Elektronentemperatur, P = Laserleistung,
Te  PLaser  Z 
2/7
Z
= mittlere Ladungszustand)
Den Zusammenhang verdeutlicht nachfolgende Graphik.
high current mode: P ~ 109 W/cm2, E ~ 1 - 50 J, t ~ 1 ns
high charge state mode: P > 1012 W/cm2, E ~ 1 - 50 J, t ~ 1 - 10 ps
WS2011/12
8.10
WS2011/12
8.11
Prinzip der Plasma-Ionenquelle:
Licht wird über einen Parabolspiegel auf das Target fokussiert (Fokusdurchmesser 65 m)
 Plasma expandiert und wird beschleunigt
 Großer Öffnungswinkel, daher zweifaches Ausblenden (vor und in expansion chamber)
Nachteile:
 große Emittanz durch die Plasmaexpansion
 große Energieverschmierung
(~10%) durch die Beschleunigung
bei der Expansion
Vorteile:
 hohe Ladungszustände
 Spitzenströme hochgeladener
Ionen bis 150 mA
WS2011/12
8.12
8.4) Elektronenkanonen
Bis in die dreißiger Jahre des letzten Jahrhunderts wurden Elektronenstrahlen nur in hochspezialisierten Anlagen und in Beschleunigern genutzt. Anfang der vierziger Jahre hielten
Elektronenstrahlen Einzug in die Hochfrequenztechnik (Klystrone, Wanderfeldröhren, Tetroden etc.).
Elektronenstrahlen werden heute in Fernseher, Elektronenmikroskopen, Schweiß- und LithographieAnlagen eingesetzt.
Ströme: A bis kA
Strahlenergien: 0.1 bis 200 keV
Bei hohen Strahlströmen muß der Einfluss der Raumladung berücksichtigt werden.
Einfaches Diodensystem:
Verzerrung der Äquipotentiallinien durch Raumladung.
Kathode
-
d
Anode
+
U
UA
Raumladung stellt sich so ein,
daß die Kathode nichts mehr
von der Anodenspannung
sieht --> Abschirmung
dU
dx
0
x 0
WS2011/12
x
d
8.13
 2U

j
j
1
U  2   

x
 0 v   0  0 2me U
Poissongleichung:
U  A  xn
Lösungsansatz:
=>
n4
3
und
U   A  n(n  1)  xn  2
=>
9 j
A
 4  0 2e
m





2
3
mit der Randbedingung
UA  A d 4/3
Damit erhält man im sogenannten "raumladungsbegrenzten Bereich" für die Emissionsstromdichte:
4
j  0
9
mit
I  j*F
2e
m
U A3 / 2
d2
 Child-Langmuir-Gesetz
F = emittierende Fläche
I  P U 3 / 2
mit P = Perveanz
Im Falle eines planaren Diodensystems ist
WS2011/12
(8.2)
4
P  0
9
2e
m
(8.3)
F
d2
8.14
Im Falle von Zylinder- oder Kugelsymmetrie: Lösungen von Langmuir und Blodgett
16
2e U A3 / 2
I    0
9
m 2
Mit
4
jc   0
9
2e
m
 Kugelsymmetrie
U A3 / 2
(rc  r )2
folgt
jKugel
8
2e U A3 / 2
I    0
9
m  2r
(rc  r )2
 jc 2 2
r
und
 Zylindersymmetrie
(rc  r )2
jZylinder  jc 2 2
r 
Dabei ist rc der Kathodenradius und (r) und (r) können als Reihenentwicklungen dargestellt werden.
3
3
63 4
13311 5 27  10391 6
   2  3 
 
 

5
10
40
4400
6160000
10472  10
r
mit
  ln  
 rc 
Erzeugung von Elektronenstrahlen:
 thermionische Emission
    A 
2
j

A

b

T
exp

  2  (8.4)
Richardson-Dushman Beziehung für die Stromdichte: R
kT

  cm 
WS2011/12
8.15
Dabei ist die Konstante
4  m e k 2
 A 
A

120
,
4
 cm 2 K 2 
h3
b = Materialabhängige Konstante
 ist die Austrittsarbeit, kT die thermische Energie der Elektronen
j wird nur messbar, wenn T >> Raumtemperatur
Typische Dioden Kennlinie:
Die Bereiche sind
a) der Anlaufstrombereich
b) der Raumladungsbereich (Child-Langmuir)
c) der Sättigungs- oder temperaturbegrenzter
Bereich
d) ist der Punkt, ab dem die Kennlinie von
Child-Langmuir abweicht.
WS2011/12
8.16
 Feldemission
E-Felder in der Größenordnung von 107 V/cm
(z.B. an Spitzen, Nadelkathoden), dabei wird das
Potential an der Festkörperoberfläche soweit
abgesenkt, dass die Elektronen hindurchtunneln
können.
-> Fowler-Nordheim Gleichung:
j FE 
K1U 2

 K   A 
exp   2   2 
 U   cm 
(8.5)
 ist die Austrittsarbeit, U die angelegte Spannung
und K1 und K2 Konstanten
Strahlformierung in Elektronenkanonen:
y
U  A  x4 / 3 ,
Wie formt man einen parallelen
Elektronenstrahl unter Raumladungseinfluss?
An der Strahlgrenze müssen
U  A x
WS2011/12
4/3
und
U
 Ey  0
y
gelten.
0
U
0
y
Kathode
U
0
y
Strahlgrenze
Strahl
 2U  2U
 2 0
x 2
y
 2U  2U

 2 
2
x
y
0
x
8.17
Das ist eine Cauchy-Randbedingung, bei der die Feldstärke vorgegeben ist!
Es gilt in diesem Fall allgemein: U
y 0
 f ( x) ,
U
y
0
y 0
Das Potential außerhalb der x-Achse (y  0) ist die analytische Fortsetzung der Funktion f(x) in die
komplexe Ebene:
U ( x, y )  Re( f ( z ))  Re( f ( x  iy ))
(iy )2


Taylorentwicklung: f ( x  iy )  f ( x)  iy  f ( x)  2! f ( x)  

U
y
y2
U ( x, y )  f ( x ) 
f ( x)   , U ( x,0)  f ( x) ,
2
  y  f ( x) y  0  0
y 0
Für den Strahlrand gilt daher
U ( x, y )  Re( A  ( x  iy ) 4 / 3 )  Ar 4 / 3 Re(exp( 43 i ))

4/3
cos( 43  )  A x 2  y 2
==> U ( x, y )  A  r
WS2011/12

2/3

cos 43 arctan( xy )

8.18
Das Kathodenpotential Uc = 0 muß überall bei
cos 43    0
sein.
Daher folgt für den Winkel:

3 9
,
8 8
oder
  67.5, 202.5
Der Randanschluss an die Kathode muß in
einem Winkel von 67.5o gegen die Flächennormale
der Kathode erfolgen, um die Divergenz eines
raumladungsdominierten Strahls zu kompensieren.
 Randelektrode mit Piercerand
WS2011/12
8.19
Strahlformierung mit Pierce-Rand gerechnet
für eine Anodenspannung von 1000 V.
1 mm entspricht 4 Maschen!
Perveanz einer solchen Kanone:
P=2.9*10-7 A/V3/2 , Strom I = 9 mA
WS2011/12
8.20
Man kann die Äquipotentialinien auch mit einem Wehneltzylinder formen.
Dabei wird das Potential an der Wehnelt-Elektrode so eingestellt, dass die Äquipotentiallinie,
welche das Kathodenpotential repräsentiert, im Piercewinkel an die Kathodenecke anschließt.
Wehneltzylinder finden in Elektronenmikroskopen und Fernsehgeräten ihre Anwendung.
WS2011/12
8.21