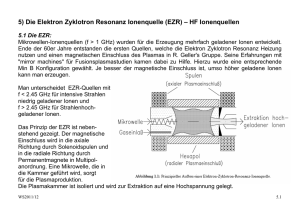
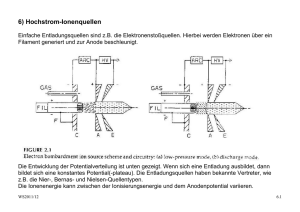
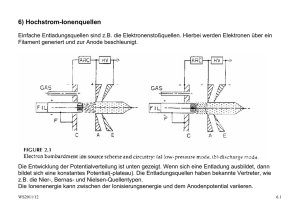
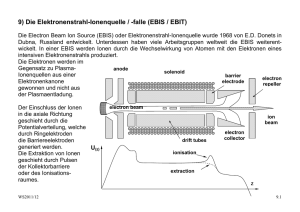
Umweltphysik / Atmosphäre V2: Struktur der Atmosphäre WS 2011
Werbung

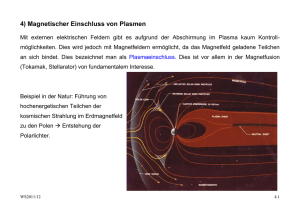
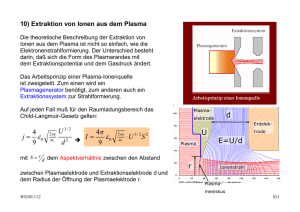
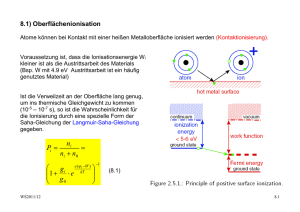
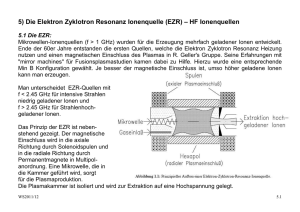
Umweltphysik / Atmosphäre V2: Struktur der Atmosphäre WS 2011/12 - Temperaturgradient - Vertikales Temperaturprofil Trockenadiabatischer T-Gradient, potentielle Temperatur Feuchtadiabatischer T-Gradient Stockwerkaufbau der Atmosphäre - Schichtungsstabilität Quantitative Überlegungen, Inversionen Konvektiv turbulente Durchmischung , Hebung und Senkung Feuchtelabilität und Äquivalenttemperatur v2-struktur.der.atmosphäre.doc 1/13 WS2011.12 Barometrische Höhenformel v2-struktur.der.atmosphäre.doc 2/13 WS2011.12 Näherungsweise Berücksichtigung der Abhängigkeit der Temperatur von der Seehöhe: Skalenhöhe Halbwertshöhe v2-struktur.der.atmosphäre.doc 3/13 WS2011.12 Gesamtmasse Tab: Skalenhöhe (Säulenhöhen) der Luftanteile Trocken - adiabatischer Temperaturgradient - Temperaturprofil in der Troposphäre: annähernd adiabatisch = kein Wärmeaustausch - Kondensation von Wasserdampf setzt latente Wärme frei - Zur Bestimmung des troposphärischen T-Profiles wird benötigt: - Ideales Gasgesetz - 1. HS der Thermodynamik - Phasendiagramm des Wassers, Dampfdruckkurve T-Profil der Troposphäre: - Aufheizung der Erdoberfläche durch Solareinstrahlung: dadurch entsteht Konvektion = adiabatischer Aufstieg - Strahlungskühlung und Strahlungsheizung der Luft ist gering im Vergleich zum Wärmetransport durch Konvektion v2-struktur.der.atmosphäre.doc 4/13 WS2011.12 Radiative Erwärmung und Abkühlung in der Atmosphäre (links) und Temperaturprofil für Troposphäre und Stratosphäre (rechts) Adiabatische Ideales Gasgesetz: 1. HS Wärmelehre pV = RT U=Q+W dU = dQ + dW dW = -p.dV dQ = 0 dU = Cv.dT Cp = Cv+R dU = -p.dV 2. Ideales Gasgesetz; totales Differential d d ( pV ) = ( RT ) dT dT dV dp p +V =R dT dT p.dV = R.dT − V .dp Cv dT = V .dp − R.dT Cv dT + R.dT = V .dp C p dT = − v2-struktur.der.atmosphäre.doc M ρ ρ . g.dz 5/13 WS2011.12 dT M .g =− dz Cp Potentielle Temperatur Poisson Gleichungen für adiabatische Zustandsänderung χ= Cp Cv χ −1 T ,V : T ⎛V ⎞ =⎜ ⎟ T0 ⎜⎝ V0 ⎟⎠ p, T : T ⎛ p0 ⎞ =⎜ ⎟ T0 ⎜⎝ p ⎟⎠ p ,V : p.V χ = p0 .V0 χ −1 χ χ Absolute Feuchte bzw. Wasserdampfdichte ρW bei Sättigung über flüssigem Wasser (durchgezogene Kurve, linke Ordinate) als Funktion der Temperatur; gestrichelt, mit der Ordinate rechts, ist der zugehörige WasserdampfPartialdruck E eingezeichnet v2-struktur.der.atmosphäre.doc 6/13 WS2011.12 Vereinfachtes und idealisiertes Modell des alpinen Föhns Mittlere Temperaturgradienten in Bodennähe als Funktion der Tageszeit, für drei verschiedene Höhenbereiche (a–c). Linke Skala: Zahlenwerte (K/m); rechte Skala: Verhältnis der aktuellen Gradienten zu dem trocken-adiabatischen Gradienten (Nach Best 1935; Best et al. 1952) v2-struktur.der.atmosphäre.doc 7/13 WS2011.12 Feucht adiabatischer Temperaturgradient dT/dzw Parameter Dampfdruck [hPa] - Partieller H2O-Dampfdruck: e - p = Σipi = ptrocken + e - Annahme: H2O sei ein ideales Gas Sättigungsdampfdruck des Wassers [hPa] es oder e* Absolute Feuchtigkeit [g/m³] a = ρv = mv/V Spezifische Feuchtigkeit [kg/kg] s oder q = ρv/ρL, mit ρL der Dichte der feuchten Luft Relative Feuchtigkeit f = e/es Taupunkt T bei e = es (p = konstant) Phasendiagramm des Wassers v2-struktur.der.atmosphäre.doc 8/13 WS2011.12 Phasenübergang von Phase 1 → Phase 2 wird durch die ClausiusClapeyron’sche Gleichung beschrieben: L12 dp = dT T ( v1 − v 2 ) L12 vi Latente Wärme beim Phasenübergang 1/ρi, spezifische Volumina Für den Übergang: H20-Dampf → Wasser gilt: v2 = vw << vd; vd = Daraus ergibt sich: Rv T p dp Lp = dT RT ² Rv = R/Mw = 8.314472 J (K.mol)/18.01 g/mol = 461.6 J/(kg.K) Die Integration ergibt: ln p s (T ) L⎛1 1 ⎞ = − ⎜⎜ − ⎟⎟ p s (To ) R ⎝ T To ⎠ ps (T ) = po ⋅ e ⎡ L⎛ 1 1 ⎢ − ⎜⎜ − ⎣⎢ R ⎝ T To ⎞⎤ ⎟⎟ ⎥ ⎠ ⎦⎥ Faustregel: ΔT = 10°K → e = 2e Wasserdampfdruck psat über Wasser, Näherungsformel von Magnus Teten. (für Eis fast identisch) psat( T) := 6.11 ⋅10 7.5⋅T 238+T 50 40 30 psat ( x) 20 10 0 20 10 0 * v2-struktur.der.atmosphäre.doc 10 20 30 x 9/13 WS2011.12 Atmosphärische Energie Kinetische Energie pro Volumen J/m³ E = ρL/2.v²; ρ = 1.29kg/m³ Fühlbare Wärme pro Volumen Qf = ρL.cp.ΔT; cp = 10³ J/(kg.K) Latente Wärme pro Volumen QL = ρL.L.q; L = 2.256.106 J/kg; s = [g/kg]; Feuchteanteil Äquivalent-Temperatur Die Äquivalenttempertatur Teq ist die fiktive Temperatur der feuchten Luft bei Kondensation des gesamten Wasserdampfes Freisetzung von Latenter Wärme pro Volumen ΔQ = ρv.L Führt zur Erhöhung der Inneren Energie U ΔU = ρL.cp. ΔT Und zu einem Temperaturanstieg entsprechend: ΔT = L ρv L =s ρ Lc p cp Feucht-adiabatischer T-Gradient - Die Freisetzung von latenter Wärme durch Kondensation wird berücksichtigt dρ w, sat =L dT dT =− dz M ⋅g RLT dρ w, sat cp + ⋅ p dT v2-struktur.der.atmosphäre.doc 10/13 WS2011.12 Feuchtadiabatischer Temperaturgradient als Funktion der Temperatur, mit dem Luftdruck als Parameter Typische mittlere Temperaturverteilung in einem Meridionalschnitt durch die nördliche Hemisphäre, links für den Winter, rechts für den Sommer. Die durchgezogenen Linien stellen Isothermen im 10◦-Abstand dar, die schräg schraffierten Balken kennzeichnen die Lage der Tropopause. (Nach Möller 1973) v2-struktur.der.atmosphäre.doc 11/13 WS2011.12 Temperaturprofil und StockwerkAufbau der Atmosphäre bis etwa 100 km Höhe. Die links in die Abb. eingezeichneten Marken geben den prozentualen Anteil der Restmasse oberhalb der jeweiligen Höhe an der Gesamtmasse der Atmosphäre an Temperaturprofil und Stockwerk-Aufbau der Atmosphäre bis etwa 100 km Höhe. Die links in die Abb. eingezeichneten Marken geben den prozentualen Anteil der Restmasse oberhalb der jeweiligen Höhe an der Gesamtmasse der Atmosphäre an Skizze zur Schichtungsstabilität, links für den Fall stabiler Schichtung, rechts für labile Schichtung. Die durchgezogene Linie stellt die Adiabate dar, auf der das Luftpaket verschoben wird, die strichpunktierte Gerade kennzeichnet den Verlauf der Umgebungstemperatur Entstehung von Absinkinversione n über Tälern; links eine schematische Skizze, rechts mögliche Temperaturprofile (T und z in willkürlichen Einheiten v2-struktur.der.atmosphäre.doc 12/13 WS2011.12 Schematisches Temperaturprofil einer Grundschichtinversion mit T und z in willkürlichen Einheiten Verstärkung der Nichtadiabasie bei kollektiver Abwärtsbewegung (bzw. Abschwächung der Nichtadiabasie bei kollektiver Aufwärtsbewegung). Horizontale Linien: Isobaren als gedachte Schichtbegrenzungen; gestrichelte Linien: adiabatischer Temperaturverlauf; schräge durchgezogene Linien: Beispiele aktueller Temperaturverläufe (1 und 2 mit überadiabatischer labiler Schichtung, 3 mit neutraler Schichtung, 4 und 5 mit unteradiabatischer stabiler Schichtung) v2-struktur.der.atmosphäre.doc 13/13 WS2011.12